


2022-2023学年上海市徐汇区田林第二中学七下数学期末学业水平测试试题含答案
展开2022-2023学年上海市徐汇区田林第二中学七下数学期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
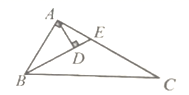
2.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交于点
交于点![]() ,
,![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 在线段
在线段![]() 的垂直平分线上,其中正确的个数有( )
的垂直平分线上,其中正确的个数有( )
A.4个 B.3个 C.2个 D.1个
3.下列各数中,是不等式![]() 的解的是
的解的是![]()
![]()
A.![]() B.0 C.1 D.3
B.0 C.1 D.3
4.函数 ![]() 中,自变量
中,自变量 ![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
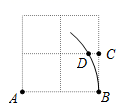
5.如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.2﹣
D.2﹣![]()
6.如果![]() ,那么yx的算术平方根是( )
,那么yx的算术平方根是( )
A.2 B.1 C.-1 D.±1
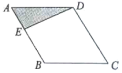
7.如图,点![]() 为菱形
为菱形![]() 边上的一个动点,并沿
边上的一个动点,并沿![]() →
→![]() →
→![]() →
→![]() 的路径移动,设点E经过的路径长为
的路径移动,设点E经过的路径长为![]() ,
,![]() 的面积为
的面积为![]() ,则下列图象能大致反映
,则下列图象能大致反映![]() 与
与![]() 的函数关系的是( )
的函数关系的是( )
A.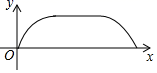 B.
B.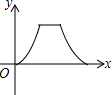
C.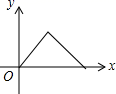 D.
D.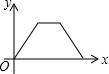
8.已知m=![]() ,n=
,n=![]() ,则代数式
,则代数式![]() 的值为 ( )
的值为 ( )
A.![]() 3 B.3 C.5 D.9
3 B.3 C.5 D.9
9.下列命题中的假命题是( )
A.一组邻边相等的平行四边形是菱形
B.一组邻边相等的矩形是正方形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等且有一个角是直角的四边形是矩形
10.过原点和点![]() 的直线的解析式为( )
的直线的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在平面直角坐标系中,点![]() 关于
关于![]() 轴对称的点的坐标是__________.
轴对称的点的坐标是__________.
12.数据1、x、-1、2的平均数是![]() ,则这组数据的方差是_______.
,则这组数据的方差是_______.
13.若关于![]() 的一元二次方程
的一元二次方程![]() 有一个根为
有一个根为![]() ,则
,则![]() ________.
________.
14.若平行四边形中两个内角的度数比为1:2,则其中一个较小的内角的度数是________°.
15.点A(a,b)是一次函数y=x+2与反比例函数![]() 的图像的交点,则
的图像的交点,则![]() __________。
__________。
16.如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是______cm.
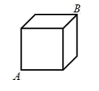
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知一次函数![]() ,当
,当![]() 时,
时,![]() ,求它的解析式以及该直线与坐标轴的交点坐标.
,求它的解析式以及该直线与坐标轴的交点坐标.
18.(8分) (1)计算: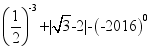
(2)先化简,再求值:![]() ,其中
,其中![]()
19.(8分)如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
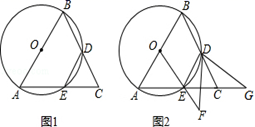
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
20.(8分)阅读下列材料,解决问题:
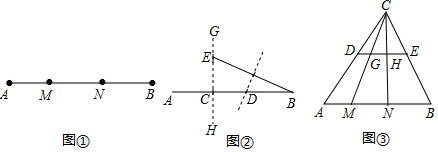
学习了勾股定理后我们知道:直角三角形两条直角边的平方和等于斜边的平方.根据勾股定理我们定义:如图①,点M、N是线段AB上两点,如果线段AM、MN、NB能构成直角三角形,则称点M、N是线段AB的勾股点
解决问题
(1)在图①中,如果AM=2,MN=3,则NB= .
(2)如图②,已知点C是线段AB上一定点(AC<BC),在线段AB上求作一点D,使得C、D是线段AB的勾股点.李玉同学是这样做的:过点C作直线GH⊥AB,在GH上截取CE=AC,连接BE,作BE的垂直平分线交AB于点D,则C、D是线段AB的勾股点你认为李玉同学的做法对吗?请说明理由
(3)如图③,DE是△ABC的中位线,M、N是AB边的勾股点(AM<MN<NB),连接CM、CN分别交DE于点G、H求证:G、H是线段DE的勾股点.
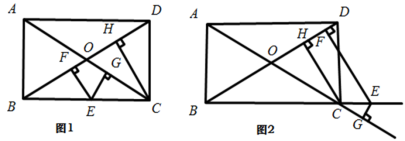
21.(8分)已知矩形![]() 中,两条对角线的交点为
中,两条对角线的交点为![]() .
.
(1)如图1,若点![]() 是
是![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,试证明:
,试证明:![]() ;
;
(2)如图②,若点![]() 在
在![]() 的延长线上,其它条件和(1)相同,则
的延长线上,其它条件和(1)相同,则![]() 三者之间具有怎样的数量关系,请写出你的结论并证明.
三者之间具有怎样的数量关系,请写出你的结论并证明.
22.(10分)某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 |
| 75 |
乙 | 78 | 80.5 |
|
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
23.(10分)第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
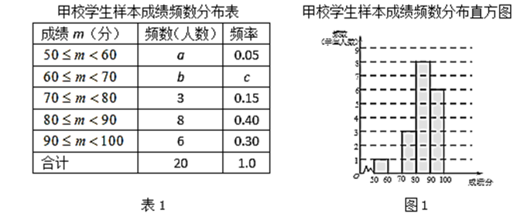
b.甲校成绩在![]() 的这一组的具体成绩是:
的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
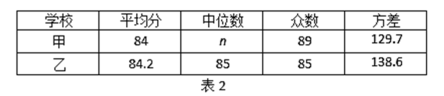
根据以上图表提供的信息,解答下列问题:
(1)表1中a = ;表2中的中位数n = ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为__________.
24.(12分)如图,在![]() 中,点
中,点![]() 是
是![]() 边的一个动点,过点
边的一个动点,过点![]() 作
作![]() ,交
,交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
,
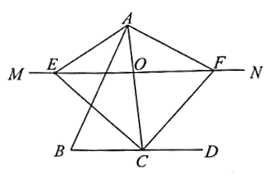
(1)求证:![]() ;
;
(2)当点![]() 位于
位于![]() 边的什么位置时四边形
边的什么位置时四边形![]() 是矩形?并说明理由.
是矩形?并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、D
4、D
5、D
6、B
7、D
8、B
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、4
14、60°
15、-8
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、该直线与x轴交点的坐标是(1,0),与y轴的交点坐标是(0,-1).
18、 (1) 9−![]() ;(2)
;(2) ![]() .
.
19、(1)证明见试题解析;(2)DF=DG.
20、(1)![]() 或
或![]() ;(2)对,理由见解析;(3)见解析
;(2)对,理由见解析;(3)见解析
21、 (1)证明见解析;(2) ![]() ,证明见解析
,证明见解析
22、(1)77.5,81;(2)乙,理由见解析.
23、(1)1,88.5;(2)见解析;(3)乙,乙的中位数是85,87>85;(4)140
24、(1)见解析;(2)当点![]() 位于
位于![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,见解析.
是矩形,见解析.
2023-2024学年上海市徐汇区田林第二中学九年级数学第一学期期末综合测试试题含答案: 这是一份2023-2024学年上海市徐汇区田林第二中学九年级数学第一学期期末综合测试试题含答案,共7页。试卷主要包含了如果,那么下列比例式中正确的是,解方程,选择最适当的方法是,一人乘雪橇沿坡度为1等内容,欢迎下载使用。
上海市民办新竹园中学2022-2023学年数学七下期末学业水平测试模拟试题含答案: 这是一份上海市民办新竹园中学2022-2023学年数学七下期末学业水平测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
2022-2023学年上海市普陀区数学七下期末学业水平测试试题含答案: 这是一份2022-2023学年上海市普陀区数学七下期末学业水平测试试题含答案,共6页。













