


2022-2023学年北京二中学教育集团数学七下期末达标测试试题含答案
展开2022-2023学年北京二中学教育集团数学七下期末达标测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各曲线中,表示![]() 是
是![]() 的函数是( )
的函数是( )
A.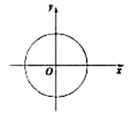 B.
B.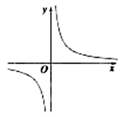 C.
C.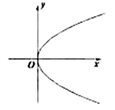 D.
D.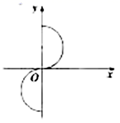
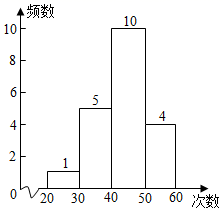
2.若甲、乙两人同时从某地出发,沿着同一个方向行走到同一个目的地,其中甲一半的路程以a(km/h)的速度行走,另一半的路程以b(km/h)的速度行走;乙一半的时间以a(km/h)的速度行走,另一半的时间以b(km/h)的速度行走(a≠b),则先到达目的地的是( )
A.甲 B.乙
C.同时到达 D.无法确定
3.如图,直线![]() 与
与![]() 的交点的横坐标为-2,则关于
的交点的横坐标为-2,则关于![]() 的不等式
的不等式![]() 的取值范围( )
的取值范围( )

A.x>-2 B.x<-2 C.-3<x<-2 D.-3<x<-1
4.下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差:
| 甲 | 乙 | 丙 | 丁 |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
5.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是9.3环,方差分别为S甲2=0.1.S乙2=0.62,S丙2=0.50,S丁2=0.45,则成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
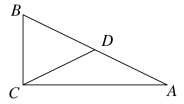
6.如图,在Rt△ABC中,CD是斜边AB上的中线.若∠A=20°,则∠BDC=( )
A.30° B.40° C.45° D.60°
7.在中山市举行“慈善万人行”大型募捐活动中,某班50位同学捐款金额统计如下:
金额(元) | 20 | 30 | 35 | 50 | 100 |
|
学生数(人) | 20 | 10 | 5 | 10 | 5 |
|
则在这次活动中,该班同学捐款金额的众数和中位数分别是( )
A.20元,30元 B.20元,35元 C.100元,35元 D.100元,30元
8.我校开展了主题为“青春·梦想”的艺术作品征集活动、从八年级某六个班中收集到的作品数量(单位:件)统计如图,则这组数据的众数、中位数、平均数依次是( )

A.48,48,48 B.48,47.5,47.5
C.48,48,48.5 D.48,47.5,48.5
9.如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )

A.1个 B.2个 C.3个 D.4个
10.在如图所示的正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果 C也是图中的格点,且使得△ABC为等腰直角三角形,则这样的点C有( )
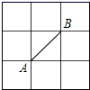
A.6个 B.7个 C.8个 D.9个
11.若函数![]() ,则当函数值y=8时,自变量x的值是( )
,则当函数值y=8时,自变量x的值是( )
A.±![]() B.4 C.±
B.4 C.±![]() 或4 D.4或-
或4 D.4或-![]()
12.下列各曲线中,不能表示y是x的函数的是( )
A. B.
B. C.
C. D.
D.
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.若样本数据1,2,3,2的平均数是a,中位数是b,众数是c,则数据a,b,c的方差是___.
14.若关于x的方程![]() +
+![]() =0有增根,则m的值是_____.
=0有增根,则m的值是_____.
15.体育张教师为了解本校八年级女生:“1分钟仰卧起坐”的达标情况,随机抽取了20名女生进行仰卧起坐测试.如图是根据测试结果绘制的频数分布直方图.如果这组数据的中位数是40次,那么仰卧起坐次数为40次的女生人数至少有__________人.
16.若分式方程![]() 有增根,则a的值为_____.
有增根,则a的值为_____.
17.如图,在平面直角坐标系中,已知![]() 顶点的坐标分别为
顶点的坐标分别为![]() ,且
,且![]() 是由
是由![]() 旋转得到.若点
旋转得到.若点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 轴上,要使四边形
轴上,要使四边形![]() 为平行四边形,则满足条件的点
为平行四边形,则满足条件的点![]() 的坐标为______.
的坐标为______.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.

19.(5分)某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
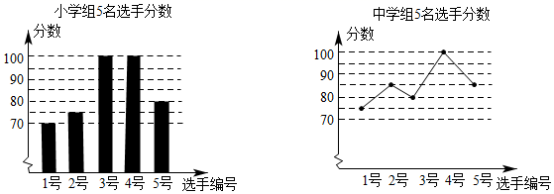
根据以上信息,整理分析数据如下:
| 平均数(分 | 中位数(分 | 众数(分 |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.
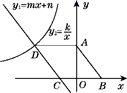
20.(8分)如图,在菱形ABCD中,AD∥x轴,点A的坐标为(0,4),点B的坐标为(3,0).CD边所在直线y1=mx+n与x轴交于点C,与双曲线y2=![]() (x<0)交于点D.
(x<0)交于点D.
(1)求直线CD对应的函数表达式及k的值.
(2)把菱形ABCD沿y轴的正方向平移多少个单位后,点C落在双曲线y2=![]() (x<0)上?
(x<0)上?
(3)直接写出使y1>y2的自变量x的取值范围.
21.(10分)在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
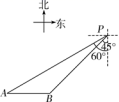
22.(10分)如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
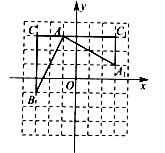
23.(12分)如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.
(x>0)与OA边交于点D、与AB边交于点E.
(1)求点D的坐标;
(2)求证:四边形ABCD是正方形;
(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.

参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、B
3、C
4、B
5、D
6、B
7、A
8、A
9、C
10、A
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、1.
14、3
15、1
16、3
17、 (−1.5,2)或(−3.5,−2)或(−0.5,4).
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)45°;(2)GF=AG+CF,证明见解析;(3)①1; ②![]() ,理由见解析.
,理由见解析.
19、(1)1,80,1;(2)从平均数和中位数进行分析,中学组代表队的决赛成绩较好;(3)中学组代表队选手成绩较稳定.
20、(1)![]() ;k=-1.(2)把菱形ABCD沿y轴的正方向平移10个单位后,点C落在双曲线上;(3)x<-5.
;k=-1.(2)把菱形ABCD沿y轴的正方向平移10个单位后,点C落在双曲线上;(3)x<-5.
21、(1)2元;(2)至少购进玫瑰200枝.
22、 (10![]() +10)海里
+10)海里
23、(1)点D的坐标为(1,1);(2)见解析;(1)![]() .
.
江苏省镇江市东部教育集团2022-2023学年七下数学期末达标检测模拟试题含答案: 这是一份江苏省镇江市东部教育集团2022-2023学年七下数学期末达标检测模拟试题含答案,共7页。试卷主要包含了方程x,关于函数,下列说法正确的是,已知,等于,在平面直角坐标系中,将点P等内容,欢迎下载使用。
广东省肇庆市高要区金利镇朝阳教育集团2022-2023学年七下数学期末达标测试试题含答案: 这是一份广东省肇庆市高要区金利镇朝阳教育集团2022-2023学年七下数学期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,在平面直角坐标系中,点,只用下列图形不,某科普小组有5名成员,身高等内容,欢迎下载使用。
北京市二中学教育集团2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案: 这是一份北京市二中学教育集团2022-2023学年数学七年级第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。













