2022-2023学年北京市丰台区长辛店第一中学七年级数学第二学期期末复习检测试题含答案

这是一份2022-2023学年北京市丰台区长辛店第一中学七年级数学第二学期期末复习检测试题含答案，共7页。
2022-2023学年北京市丰台区长辛店第一中学七年级数学第二学期期末复习检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1．设x1、x2是方程x²+x-1=0的两根，则x1+x2=（     ）A．-3 B．-1 C．1 D．32．一元二次方程x2-9=0的解为（    ）A．x1=x2=3 B．x1=x2=-3 C．x1=3，x2=-3 D．x1=，x2=-3．下列图形中，是中心对称但不是轴对称图形的有(   )A．1个 B．2个 C．3个 D．4个4．对点Q（0，3）的说法正确的是（    ）A．是第一象限的点 B．在轴的正半轴C．在轴的正半轴 D．在轴上5．用配方法解一元二次方程，下列配方正确的是（     ）A． B． C． D．6．解分式方程时，在方程的两边同时乘以（x﹣1）（x+1），把原方程化为x+1+2x（x﹣1）＝2（x﹣1）（x+1），这一变形过程体现的数学思想主要是（　　）A．类比思想 B．转化思想 C．方程思想 D．函数思想7．关于▱ABCD的叙述，正确的是（　　）A．若AB⊥BC，则▱ABCD是菱形 B．若AC⊥BD，则▱ABCD是正方形C．若AC=BD，则▱ABCD是矩形 D．若AB=AD，则▱ABCD是正方形8．如图，在Rt△ABC中，∠ACB＝90°，D、E分别是AB、AC的中点，连接CD，过E作EF∥DC交BC的延长线于F，若四边形DCFE的周长为18cm，AC的长6cm，则AD的长为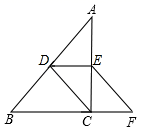（　　）A．13cm B．12cm C．5cm D．8cm9．若式子有意义，则x的取值范围为（   ）．A．x≥2 B．x≠2 C．x≤2 D．x＜210．在平面直角坐标系xOy中，已知点A（2，﹣2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的有（　　）个．A．5 B．4 C．3 D．2二、填空题(本大题共有6小题，每小题3分，共18分)11．学校篮球队五名队员的年龄分别为，其方差为，则三年后这五名队员年龄的方差为______．12．某中学组织八年级学生进行“绿色出行，低碳生活”知识竞赛，为了了解本次竞赛的成绩，把学生成绩分成五个等级，并绘制如图所示的扇形统计图(不完整)统计成绩，则等级所在扇形的圆心角是_______º.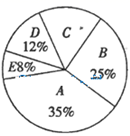13．如图，正方形CDEF内接于，，，则正方形的面积是________.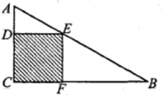14．小明从家跑步到学校，接着马上原路步行回家．如图所示为小明离家的路程与时间的图像，则小明回家的速度是每分钟步行________m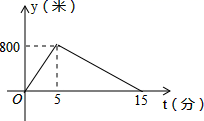．15．如果多项式是一个完全平方式，那么k的值为______．16．因式分解：a2﹣6a+9=_____．三、解下列各题(本大题共8小题，共72分)17．（8分）计算：（1）分解因式：m2（x﹣y）+4n2（y﹣x）；（2）解不等式组，并把解集在数轴上表示出来；（3）先化简，再求解， ，其中x＝﹣2.   18．（8分）问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．（发现证明）小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．（类比引申）如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足                      关系时，仍有EF=BE+FD．（探究应用）如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：=1.41，=1.73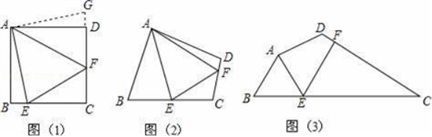）   19．（8分）已知：，，求的值．   20．（8分）如图，E、F分别平行四边形ABCD对角线BD上的点，且BE＝DF．求证：∠DAF＝∠BCE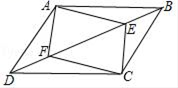．   21．（8分）一个三角形的三边长分别为5，，.(1)求它的周长(要求结果化简)；(2)请你给出一个适当的x值，使它的周长为整数，并求出此时三角形周长的值．   22．（10分）阅读下面材料：数学课上，老师出示了这祥一个问题：如图，在正方形ABCD中，点F在AB上，点E在BC延长线上。且AF=CE，连接EF，过点D作DH⊥FE于点H，连接CH并延长交BD于点0，∠BFE=75°.求的值.某学习小组的同学经过思考，交流了自己的想法：小柏：“通过观察和度量，发现点H是线段EF的中点”。小吉：“∠BFE=75°，说明图形中隐含着特殊角”；小亮：“通过观察和度量，发现CO⊥BD”；小刚：“题目中的条件是连接CH并延长交BD于点O，所以CO平分∠BCD不是己知条件。不能由三线合一得到CO⊥BD”；小杰：“利用中点作辅助线，直接或通过三角形全等，就能证出CO⊥BD，从而得到结论”；……；老师：“延长DH交BC于点G，若刪除∠BFB=75°，保留原题其余条件，取AD中点M，连接MH，如果给出AB，MH的值。那么可以求出GE的长度”.请回答：(1)证明FH=EH；(2)求的值；(3)若AB=4.MH=，则GE的长度为_____________.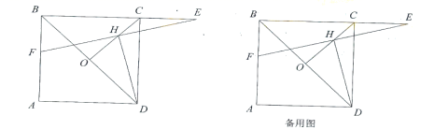   23．（10分）如图，在平行四边形ABCD中，点E、F在对角线BD上，且BF=DE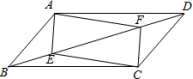（1）求证：△ADE≌△CBF.（2）若AE=3，AD=4，∠DAE=90°，该判断当BE的长度为多少时，四边形AECF为菱形，并说明理由.   24．（12分）正方形ABCD中，点O是对角线DB的中点，点P是DB所在直线上的一个动点，PE⊥BC于E，PF⊥DC于F．（1）当点P与点O重合时（如图①），猜测AP与EF的数量及位置关系，并证明你的结论；（2）当点P在线段DB上（不与点D、O、B重合）时（如图②），探究（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由；（3）当点P在DB的长延长线上时，请将图③补充完整，并判断（1）中的结论是否成立？若成立，直接写出结论；若不成立，请写出相应的结论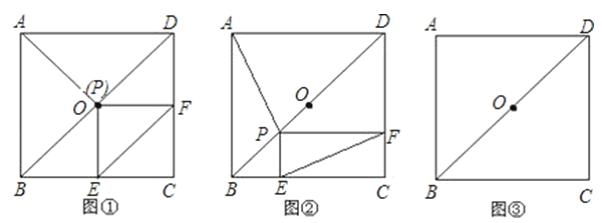．    参考答案 一、选择题(每小题3分,共30分)1、B2、C3、B4、B5、A6、B7、C8、C9、D10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、0.1．12、72°13、0.814、115、8或-416、 三、解下列各题(本大题共8小题，共72分)17、（1）（x﹣y）（m＋2n）（m－2n）；（2），见解析；（3）4－6.18、19、320、详见解析21、（1）；（2）见解析.22、（1）见解析；（2） ；（3）23、（1）证明见解析；（2）BE的长度为时，四边形AECF为菱形.24、（1）AP=EF，AP⊥EF，理由见解析；（2）仍成立，理由见解析；（3）仍成立，理由见解析；