2022-2023学年北京市海淀区首师大附七下数学期末检测试题含答案

这是一份2022-2023学年北京市海淀区首师大附七下数学期末检测试题含答案，共7页。
2022-2023学年北京市海淀区首师大附七下数学期末检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．比较A组、B组中两组数据的平均数及方差，一下说法正确的是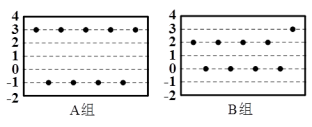（   ）A．A组，B组平均数及方差分别相等 B．A组，B组平均数相等，B组方差大C．A组比B组的平均数、方差都大 D．A组，B组平均数相等，A组方差大2．一元二次方程的根是（   ）A．x  0 B．x  1 C．x  0, x  1 D．无实根3．已知四边形ABCD是平行四边形，下列结果正确的是（     ）A．当AB=BC时，它是矩形 B．时，它是菱形C．当∠ABC=90°时，它是菱形 D．当AC=BD时，它是正方形4．如图，已知菱形ABCD的周长是24米，∠BAC＝30°，则对角线BD的长等于()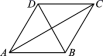A．6米 B．3米 C．6米 D．3米5．若a＝﹣0.32，b＝﹣3﹣2，c＝（﹣）﹣2，d＝（﹣）0，则（　　）A．a＜b＜c＜d B．b＜a＜d＜c C．a＜d＜c＜b D．c＜a＜d＜b6．一次函数y＝kx+b的图象如图所示，则一元一次不等式kx+b＜0的解集为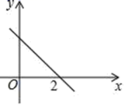（　　）A．x＜2 B．x＞2 C．x＜0 D．x＞07．已知点（﹣2，y1），（﹣1，y2），（1，y3）都在直线y=﹣3x+2上，则y1，y2，y3的值的大小关系是（  ）A．y3＜y1＜y2    B．y1＜y2＜y3    C．y3＞y1＞y2    D．y1＞y2＞y38．若m＋n－p＝0，则m的值是(　　)A．－3 B．－1 C．1 D．39．经过多边形一个角的两边剪掉这个角，则得到的新多边形的外角和（    ）A．比原多边形多 B．比原多边形少 C．与原多边形外角和相等 D．不确定10．如图，□ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为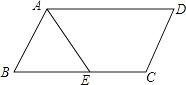（  ）A．1 B．2 C．3 D．4二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，垂直平分线段于点的平分线交于点，连结，则∠AEC的度数是 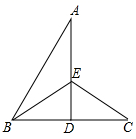       ．12．如图，将矩形ABCD沿直线BD折叠，使C点落在C′处，BC′交边AD于点E，若∠ADC′=40°，则∠ABD的度数是_____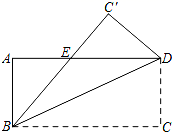．13．把直线y＝﹣2x﹣1沿x轴向右平移3个单位长度，所得直线的函数解析式为_____．14．一次函数y=2x+1的图象与x轴的交点坐标为______．15．如图，已知菱形的面积为24，正方形的面积为18，则菱形的边长是__________．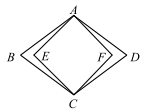16．在平行四边形ABCD中，已知∠A﹣∠B＝60°，则∠C＝_____．三、解下列各题(本大题共8小题，共72分)17．（8分）如图，在平面直角坐标系中，O 为坐标原点，P、Q 是反比例函数（x>0）图象上的两点，过点 P、Q 分别作直线且与 x、y 轴分别交于点 A、B和点 M、N．已知点 P 为线段 AB 的中点．(1)求△AOB 的面积（结果用含 a 的代数式表示）；(2)当点 Q 为线段 MN 的中点时，小菲同学连结 AN，MB 后发现此时直线 AN 与直线MB 平行，问小菲同学发现的结论正确吗？为什么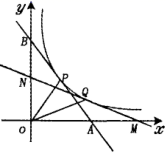？   18．（8分）如图：是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题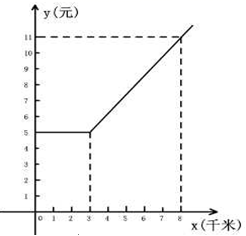：（1）当行使8千米时,收费应为       元；（2）从图象上你能获得哪些信息?(请写出2条)①                   ________②____________________________（3）求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.   19．（8分） “端午节”某顾客到商场购买商品，发现如果购买3件A商品和2件B商品共需花费230元，如果购买4件A商品和1件B商品共需花费240元．（1）求A商品、B商品的单价分别是多少元？（2）商场在“端午节”开展促销活动，促销方法是：购买A商品超过10件，超过部分可以享受6折优惠，若购买x（x＞0）件A商品需要花费y元，请你求出y与x的函数关系式．（3）在（2）的条件下，顾客决定在A、B两种商品中选购其中一种，且数量超过10件，请你帮助顾客判断买哪种商品省钱．   20．（8分）如图，一块四边形的土地，其中∠BAD=90°，AB=4m，BC=12m，CD=13m，AD=3m．（1）试说明BD⊥BC；（2）求这块土地的面积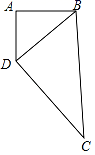．   21．（8分）如图，在平面直角坐标系中，直线y＝x和y＝﹣2x+6交于点A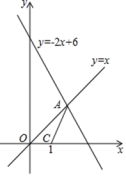．（1）求点A的坐标；（2）若点C的坐标为（1，0），连接AC，求△AOC的面积．   22．（10分）如图1，点是正方形边上任意一点，以为边作正方形，连接，点是线段中点，射线与交于点，连接．（1）请直接写出和的数量关系和位置关系．（2）把图1中的正方形绕点顺时针旋转，此时点恰好落在线段上，如图2，其他条件不变，（1）中的结论是否成立，请说明理由．（3）把图1中的正方形绕点顺时针旋转，此时点、恰好分别落在线段、 上，连接，如图3，其他条件不变，若，，直接写出的长度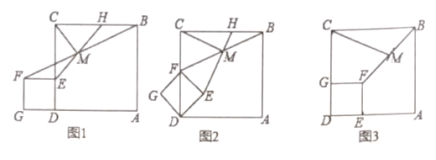．   23．（10分）已知边长为4的正方形ABCD，顶点A与坐标原点重合，一反比例函数图象过顶点C，动点P以每秒1个单位速度从点A出发沿AB方向运动，动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动，当点P与点Q相遇时停止运动，设点P的运动时间为t．（1）求出该反比例函数解析式；（2）连接PD，当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时，求点Q的坐标；（3）用含t的代数式表示以点Q、P、D为顶点的三角形的面积s，并指出相应t的取值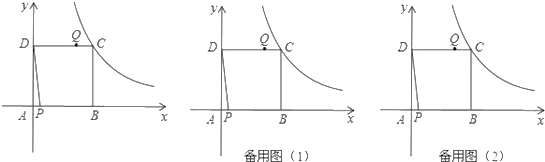．   24．（12分）据大数据统计显示，某省2016年公民出境旅游人数约100万人次，2017年与2018年两年公民出境旅游总人数约264万人次，若这两年公民出境旅游总人数逐年递增，请解答下列问题：（1）求这两年该省公民出境旅游人数的年平均增长率；（2）如果2019年仍保持相同的年平均增长率，请你预测2019年该省公民出境旅游人数约多少万人次？   参考答案 一、选择题(每小题3分,共30分)1、D2、C3、B4、C5、B6、B7、D8、A9、C10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、115°12、65°13、y＝﹣2x+114、（-，0）15、116、 三、解下列各题(本大题共8小题，共72分)17、（1）S=2a+2；（2）正确，理由见解析18、（1）11；（2）如：出租车起步价（3千米内）为5元；超出3千米，每千米加收1.2元等；（3）.19、（1）A商品、B商品的单价分别是50元、40元；（2）；（3）当购进商品少于20件，选择购B种商品省钱．20、 (1)见解析;(2)36m².21、（1）A的坐标（2，2）；（2）1.22、（1）；（2）见解析；（3）.23、（1）y=；（2）Q1（，4）；Q2（4，），Q3（4，）；（3）s1=8t（0＜t≤1）；s2=﹣2t2+2t+8（1≤t≤2）；s3=﹣10t+1（2≤t≤）．24、 (1)这两年公民出境旅游总人数的年平均增长率为20%；(2)约172.8万人次.