


2022-2023学年北京市石景山区七下数学期末考试试题含答案
展开2022-2023学年北京市石景山区七下数学期末考试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题,①4的平方根是2;②有两边和一角相等的两个三角形全等;③等腰三角形的底角必为锐角;④两组对角分别相等的四边形是平行四边形.其中真命题有( )
A.4个 B.3个 C.2个 D.1个
2.下列命题是真命题的是( )
A.对角线互相垂直的四边形是菱形 B.对角线相等的菱形是正方形
C.对角线互相垂直且相等的四边形是正方形 D.对角线相等的四边形是矩形
3.如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )
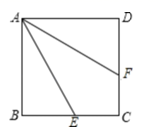
A.30° B.45° C.60° D.90°
4.在某市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
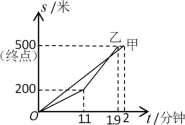
A.这次比赛的全程是500米
B.乙队先到达终点
C.比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快
D.乙与甲相遇时乙的速度是375米/分钟
5.小明用作图象的方法解二元一次方程组时,他作出了相应的两个一次函数的图象,则他解的这个方程组是( )
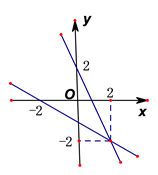
A.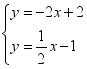 B.
B.![]() C.
C.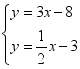 D.
D.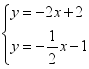
6.下列运算错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.某校艺术节的乒乓球比赛中,小东同学顺利进入决赛.有同学预测“小东夺冠的可能性是80%”,则对该同学的说法理解最合理的是( )
A.小东夺冠的可能性较大 B.如果小东和他的对手比赛10局,他一定会赢8局
C.小东夺冠的可能性较小 D.小东肯定会赢
8.以下由两个全等的30°直角三角板拼成的图形中,属于中心对称图形的是( )
A. B.
B.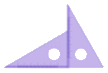
C.![]() D.
D.![]()
9.在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )
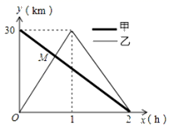
A.1个 B.2个 C.3个 D.4个
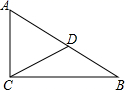
10.如图,在![]() 中,
中,![]() ,
,![]() ,点D是AB的中点,则
,点D是AB的中点,则![]()
![]()
A.4 B.5 C.6 D.8
11.在![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,则
的中点,则![]() 与
与![]() 的面积之比为
的面积之比为![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.某校八![]() 班
班![]() 名同学在
名同学在![]() 分钟投篮测试中的成绩如下:
分钟投篮测试中的成绩如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:个),则这组数据的中位数、众数分别是( )
,(单位:个),则这组数据的中位数、众数分别是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
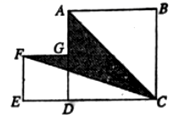
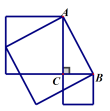
13.如图,正方形ABCD的面积等于25cm2,正方形DEFG的面积等于9cm2,则阴影部分的面积S=______cm2.
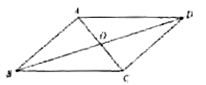
14.如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
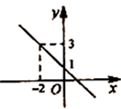
15.在平面直角坐标系中,一次函数![]() (
(![]() 、
、![]() 为常数,
为常数,![]() )的图象如图所示,根据图象中的信息可求得关于
)的图象如图所示,根据图象中的信息可求得关于![]() 的方程
的方程![]() 的解为____.
的解为____.
16.已知直角三角形![]() 中,分别以
中,分别以![]() 为边作三个正方形,其面积分别为
为边作三个正方形,其面积分别为![]() ,则
,则![]() __________
__________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
17.方程![]() 的解为:___________.
的解为:___________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)如图,以矩形![]() 的顶点
的顶点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,![]() ,
,![]() ,点
,点![]() 为
为![]() 轴上一动点,以
轴上一动点,以![]() 为一边在
为一边在![]() 右侧作正方形
右侧作正方形![]() .
.
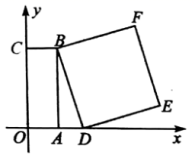
(1)若点![]() 与点
与点![]() 重合,请直接写出点
重合,请直接写出点![]() 的坐标.
的坐标.
(2)若点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.
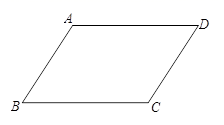
19.(5分)如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则CE= .
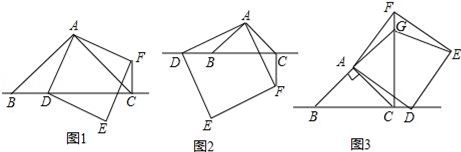
20.(8分)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.
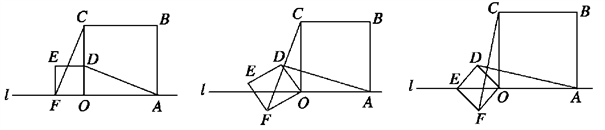
21.(10分)小明在数学活动课上,将边长为![]() 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
![]()
22.(10分)甲、乙两名队员参加射击训练,成绩分别被作成下列两个统计图:
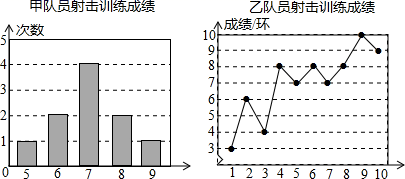
根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)请计算甲的平均成绩,乙的训练成绩的中位数和方差;(列式解答)
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
23.(12分)已知:线段![]() 、
、![]() .
.
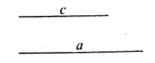
求作:![]() ,使
,使![]() ,
,![]() ,
,![]()
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、B
3、A
4、C
5、D
6、C
7、A
8、D
9、C
10、B
11、C
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、1
15、x=-2
16、![]()
17、![]() ,
,![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
19、(1)见解析;(2)1.
20、(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3)![]() .
.
21、(2)详见解析(2)CF=![]()
22、(1)甲的平均成绩为7环,乙射击成绩的中位数为7.5环,方差为![]() ;(2)详见解析.
;(2)详见解析.
23、见解析
北京市石景山区2023-2024学年数学九上期末考试模拟试题含答案: 这是一份北京市石景山区2023-2024学年数学九上期末考试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,某班7名女生的体重等内容,欢迎下载使用。
北京市石景山区景山学校2022-2023学年数学七下期末质量检测模拟试题含答案: 这是一份北京市石景山区景山学校2022-2023学年数学七下期末质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,反比例函数经过点等内容,欢迎下载使用。
北京市石景山区2022-2023学年数学七下期末达标测试试题含答案: 这是一份北京市石景山区2022-2023学年数学七下期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,函数y=中自变量x的取值范围是,若分式有意义,则的取值范围是,下列计算或化简正确的是等内容,欢迎下载使用。













