


2022-2023学年呼伦贝尔市重点中学数学七年级第二学期期末综合测试模拟试题含答案
展开
这是一份2022-2023学年呼伦贝尔市重点中学数学七年级第二学期期末综合测试模拟试题含答案,共9页。
2022-2023学年呼伦贝尔市重点中学数学七年级第二学期期末综合测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.如图,菱形![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,则菱形的边长为( )
,则菱形的边长为( )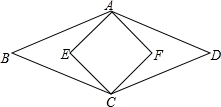 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.如图,在菱形
2.如图,在菱形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,
上的动点,![]() ,点
,点![]() 从点
从点![]() 向点
向点![]() 运动的过程中,
运动的过程中,![]() 的长度( )
的长度( )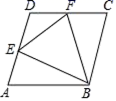 A.逐渐增加 B.逐渐减小C.保持不变且与
A.逐渐增加 B.逐渐减小C.保持不变且与![]() 的长度相等 D.保持不变且与
的长度相等 D.保持不变且与![]() 的长度相等3.如图,直线y=x+
的长度相等3.如图,直线y=x+![]() 与y=kx-1相交于点P,点P的纵坐标为
与y=kx-1相交于点P,点P的纵坐标为![]() ,则关于x的不等式x+
,则关于x的不等式x+![]() >kx-1的解集在数轴上表示正确的是( )
>kx-1的解集在数轴上表示正确的是( )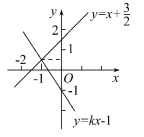 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如图,在平面直角坐标系
4.如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
 A.1个 B.2个 C.3个 D.4个5.下列事件:①上海明天是晴天,②铅球浮在水面上,③平面中,多边形的外角和都等于360度,属于确定事件的个数有( )A.0个 B.1个 C.2个 D.3个6.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )
A.1个 B.2个 C.3个 D.4个5.下列事件:①上海明天是晴天,②铅球浮在水面上,③平面中,多边形的外角和都等于360度,属于确定事件的个数有( )A.0个 B.1个 C.2个 D.3个6.如图,任意转动正六边形转盘一次,当转盘停止转动时,指针指向大于3的数的概率是( )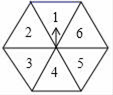 A.
A.![]() B.
B.![]() C.
C.![]() D.
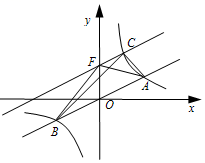
D.![]() 7.如图所示,已知点C(1,0),直线
7.如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )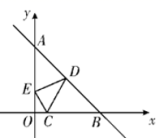 A.
A.![]() B.10C.
B.10C.![]() D.128.如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A、C两点之间的距离为( )
D.128.如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A、C两点之间的距离为( )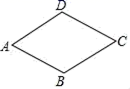 A.4米 B.4
A.4米 B.4![]() 米 C.8米 D.8
米 C.8米 D.8![]() 米9.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )
米9.如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( )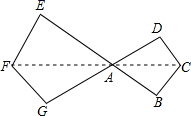 A.四边形ABCD与四边形AEFG是相似图形B.AD与AE的比是2:3C.四边形ABCD与四边形AEFG的周长比是2:3D.四边形ABCD与四边形AEFG的面积比是4:910.下列图形中,既是中心对称图形也是轴对称图形的是( )A.
A.四边形ABCD与四边形AEFG是相似图形B.AD与AE的比是2:3C.四边形ABCD与四边形AEFG的周长比是2:3D.四边形ABCD与四边形AEFG的面积比是4:910.下列图形中,既是中心对称图形也是轴对称图形的是( )A. B.
B. C.
C. D.
D. 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,平行四边形ABCO的顶点O,A,C的坐标分别是(0,0),(a,0),(b,c),则顶点坐标B的坐标为_________.
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,平行四边形ABCO的顶点O,A,C的坐标分别是(0,0),(a,0),(b,c),则顶点坐标B的坐标为_________.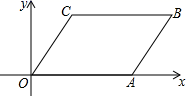 12.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差: 甲乙丙丁平均数
12.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差: 甲乙丙丁平均数![]()
![]()
![]()
![]()
![]() 方差
方差![]()
![]()
![]()
![]()
![]() 根据表中数据,要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛,应该选择__________.13.如图,直线y=
根据表中数据,要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛,应该选择__________.13.如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为_____.
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为_____.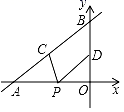 14.已知二次函数
14.已知二次函数![]() 的图象与
的图象与![]() 轴没有交点,则
轴没有交点,则![]() 的取值范围是_____.15.如图,沿折痕AE折叠矩形ABCD的一边,使点D落在BC边上一点F处.若AB=8,且△ABF的面积为24,则EC的长为__.
的取值范围是_____.15.如图,沿折痕AE折叠矩形ABCD的一边,使点D落在BC边上一点F处.若AB=8,且△ABF的面积为24,则EC的长为__.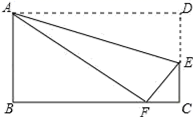 16.如图,已知:∠MON=30°,点A
16.如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____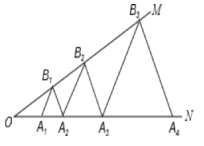 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,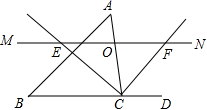 (1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由. 18.(8分)甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:
(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由. 18.(8分)甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示: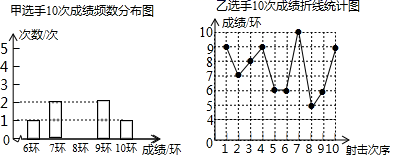 根据以上信息,请解答下面的问题;选手A平均数中位数众数方差甲a88c乙7.5b6和92.65(1)补全甲选手10次成绩频数分布图.(2)a= ,b= ,c= .(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由). 19.(8分)如图,直线l1的解析式为y=-x+4,直线l2的解析式为y=x-2,l1和l2的交点为点B.
根据以上信息,请解答下面的问题;选手A平均数中位数众数方差甲a88c乙7.5b6和92.65(1)补全甲选手10次成绩频数分布图.(2)a= ,b= ,c= .(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由). 19.(8分)如图,直线l1的解析式为y=-x+4,直线l2的解析式为y=x-2,l1和l2的交点为点B.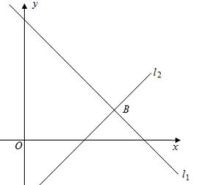 (1)直接写出点B坐标;(2)平行于y轴的直线交x轴于点M,交直线l1于E,交直线l2于F. ①分别求出当x =2和x =4时E F的值. ②直接写出线段E F的长y与x的函数关系式,并画出函数图像L. ③在②的条件下,如果直线y=kx+b与L只有一个公共点,直接写出k的取值范围. 20.(8分)(1)如图甲,从边长为a的正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形,然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证因式分解公式成立的是________;
(1)直接写出点B坐标;(2)平行于y轴的直线交x轴于点M,交直线l1于E,交直线l2于F. ①分别求出当x =2和x =4时E F的值. ②直接写出线段E F的长y与x的函数关系式,并画出函数图像L. ③在②的条件下,如果直线y=kx+b与L只有一个公共点,直接写出k的取值范围. 20.(8分)(1)如图甲,从边长为a的正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形,然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证因式分解公式成立的是________;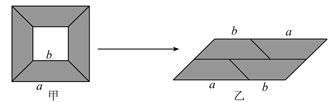 (2)根据下面四个算式:5232=(5+3)×(53)=8×2;11252=(11+5)×(115)=16×6=8×12;15232=(15+3)×(153)=18×12=8×27;19272=(19+7)×(197)=26×12=8×1.请你再写出两个(不同于上面算式)具有上述规律的算式;(3)用文字写出反映(2)中算式的规律,并证明这个规律的正确性. 21.(8分)计算:(1)|1-2
(2)根据下面四个算式:5232=(5+3)×(53)=8×2;11252=(11+5)×(115)=16×6=8×12;15232=(15+3)×(153)=18×12=8×27;19272=(19+7)×(197)=26×12=8×1.请你再写出两个(不同于上面算式)具有上述规律的算式;(3)用文字写出反映(2)中算式的规律,并证明这个规律的正确性. 21.(8分)计算:(1)|1-2![]() |+
|+![]() .(2)
.(2)![]() 22.(10分)解方程:x2-1= 4x 23.(10分)如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.(1)求证:四边形ABCD是矩形;(2)若DE=3,OE=9,求AB、AD的长;
22.(10分)解方程:x2-1= 4x 23.(10分)如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.(1)求证:四边形ABCD是矩形;(2)若DE=3,OE=9,求AB、AD的长;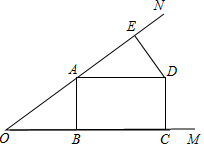 24.(12分)为了从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4乙:9、5、7、8、7、6、8、6、7、7如果你是教练你会选拔谁参加比赛?为什么? 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、A4、C5、C6、D7、B8、D9、B10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、 (a+b,c)12、丙13、(
24.(12分)为了从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶10次,命中的环数如下:甲:7、8、6、8、6、5、9、10、7、4乙:9、5、7、8、7、6、8、6、7、7如果你是教练你会选拔谁参加比赛?为什么? 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、A4、C5、C6、D7、B8、D9、B10、D 二、填空题(本大题共有6小题,每小题3分,共18分)11、 (a+b,c)12、丙13、(![]() ,0)14、
,0)14、![]() 15、216、32 三、解下列各题(本大题共8小题,共72分)17、解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
15、216、32 三、解下列各题(本大题共8小题,共72分)17、解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,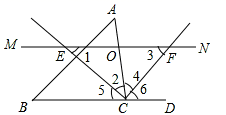 ∴∠2=∠3,2=∠1.∵MN∥BC,∴∠1=∠3,3=∠1.∴∠1=∠2,∠3=∠2.∴EO=CO,FO=CO.∴OE=OF.(2)∵∠2=∠3,∠2=∠1,∴∠2+∠2=∠3+∠1=90°.∵CE=12,CF=3,∴
∴∠2=∠3,2=∠1.∵MN∥BC,∴∠1=∠3,3=∠1.∴∠1=∠2,∠3=∠2.∴EO=CO,FO=CO.∴OE=OF.(2)∵∠2=∠3,∠2=∠1,∴∠2+∠2=∠3+∠1=90°.∵CE=12,CF=3,∴![]() .∴OC=
.∴OC=![]() EF=1.3.(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形.∵∠ECF=90°,∴平行四边形AECF是矩形.18、(1)4;(2)8、1.2、7.5;(3)从平均数看,甲成绩优于乙的成绩;从方差看,甲的方差小,说明甲的成绩稳定.19、(1)(3,1);(2)①EF=2;②见解析. ③k >2或k<-2或.k=-
EF=1.3.(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形.∵∠ECF=90°,∴平行四边形AECF是矩形.18、(1)4;(2)8、1.2、7.5;(3)从平均数看,甲成绩优于乙的成绩;从方差看,甲的方差小,说明甲的成绩稳定.19、(1)(3,1);(2)①EF=2;②见解析. ③k >2或k<-2或.k=-![]() 20、(1)a2-b2=(a+b)(ab);(2)72-52=8×3;92-32=8×9等;(3)规律:任意两个奇数的平方差是8的倍数,证明见解析21、(1)0;(2)
20、(1)a2-b2=(a+b)(ab);(2)72-52=8×3;92-32=8×9等;(3)规律:任意两个奇数的平方差是8的倍数,证明见解析21、(1)0;(2)![]() .22、
.22、![]() 23、 (1) 见解析;(2) AB、AD的长分别为3和124、乙同学的成绩较稳定,应选乙参加比赛
23、 (1) 见解析;(2) AB、AD的长分别为3和124、乙同学的成绩较稳定,应选乙参加比赛
相关试卷
这是一份2022-2023学年肇庆市重点中学数学七年级第二学期期末监测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,已知A等内容,欢迎下载使用。
这是一份2022-2023学年菏泽市重点中学数学七年级第二学期期末联考模拟试题含答案,共6页。试卷主要包含了已知下面四个方程,下列图形中,成中心对称图形的是,使等式成立的x的值是等内容,欢迎下载使用。
这是一份2022-2023学年石嘴山市重点中学数学七年级第二学期期末综合测试模拟试题含答案,共5页。试卷主要包含了答题时请按要求用笔,下列命题中正确的是,已知的三边,,满足,则的面积为等内容,欢迎下载使用。









