2022-2023学年四川省资阳市名校七下数学期末教学质量检测模拟试题含答案

这是一份2022-2023学年四川省资阳市名校七下数学期末教学质量检测模拟试题含答案，共8页。
2022-2023学年四川省资阳市名校七下数学期末教学质量检测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的( 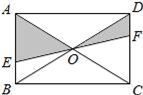  )A． B． C． D．2．小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示，现在他将正方形从当前位置开始进行一次平移操作，平移后的正方形的顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有( 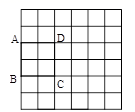 )A．3个 B．4个 C．5个 D．无数个3．如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点．且BE＝CF，连接BF、DE，则BF+DE的最小值为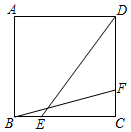（    ）A． B． C． D．4．已知x=，y=，则x2+xy+y2的值为（　　）A．2 B．4 C．5 D．75．已知点，、，是直线上的两点，下列判断中正确的是（    ）A． B． C．当时， D．当时，6．若函数y=kx+b的图象如图所示，则关于x的不等式kx+b>0的解集为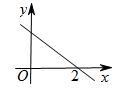（   ）A．x＜2 B．x＞2 C．x≤2 D．x≥27．如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC；其中正确结论的个数为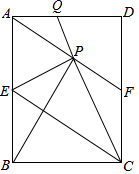（　　）A．1 B．2 C．3 D．48．某星期六上午，小明从家出发跑步去公园，在公园停留了一会儿打车回家．图中折线表 示小明离开家的路程y（米）和所用时间x（分）之间的函数关系，则下列说法中错误的是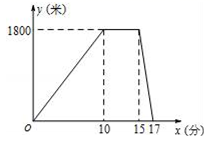（ ）A．小明在公园休息了5分钟B．小明乘出租车用了17分C．小明跑步的速度为180米/分D．出租车的平均速度是900米/分9．在相同时刻，物高与影长成正比．如果高为1.5米的标杆影长为2.5米，那么此时高为18米的旗杆的影长为（    ）A．20米 B．30米 C．16米 D．15米10．在，，，，，中分式的个数有（    ）A．2个 B．3个 C．4个 D．5个11．下列事件中，属于必然事件的是（）A．经过路口，恰好遇到红灯； B．四个人分成三组，三组中有一组必有2人；C．打开电视，正在播放动画片； D．抛一枚硬币，正面朝上；12．下列计算结果正确的是　　A． B． C． D．二、填空题（每题4分，满分20分，将答案填在答题纸上）13．某校要从甲、乙两名跳远运动员挑选一人参加校际比赛．在十次选拔比赛中，他们的方差分别为S甲2=1．32，S乙2=1．26，则应选________参加这项比赛(填“甲”或者“乙”)14．如图，一次函数与的图的交点坐标为（2，3），则关于的不等式的解集为_____. 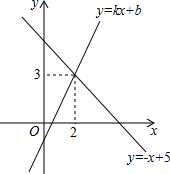15．函数y=-x，在x=10时的函数值是______．16．在正方形中,点在边上，点在线段上，且则_______度，四边形的面积_________.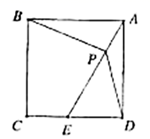17．若分式的值为0，则的值为________．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：“宇番2号”番茄挂果数量统计表挂果数量x（个）
 频数（株）
 频率
 25≤x＜35
 6
 0.1
 35≤x＜45
 12
 0.2
 45≤x＜55
 a
 0.25
 55≤x＜65
 18
 b
 65≤x＜75
 9
 0.15
 请结合图表中的信息解答下列问题：（1）统计表中，a=     ，b=     ；（2）将频数分布直方图补充完整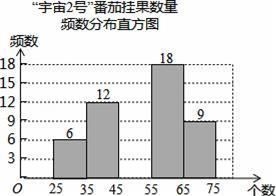；（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为     °；（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有     株．   19．（5分）如图①，四边形和四边形都是正方形，且，，正方形固定，将正方形绕点顺时针旋转角()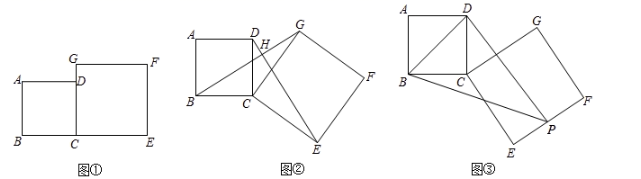．（1）如图②，连接、，相交于点，请判断和是否相等？并说明理由；（2）如图②，连接，在旋转过程中，当为直角三角形时，请直接写出旋转角的度数；（3）如图③，点为边的中点，连接、、，在正方形的旋转过程中，的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．   20．（8分）如图，平行四边形中，，点、分别在、的延长线上，，，垂足为点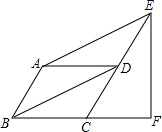，.（1）求证：是中点；（2）求的长.   21．（10分）某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：每人加工件数540450300240210120人数112632（1）写出这15人该月加工零件数的平均数、中位数和众数．（2）若以本次统计所得的月加工零件数的平均数定为每位工人每月的生产定额，你认为这个定额是否合理，为什么？   22．（10分）如图，正方形网格中每个小正方形的边长都是1个单位长度，每个小正方形的顶点叫做格点，已知△ABC的三个顶点都是格点，请按要求画出三角形.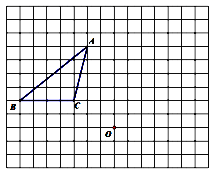（1）将△ABC先上平移1个单位长度再向右平移2个单位长度，得到△A'B'C'；（2）将△A'B'C'绕格点O顺时针旋转90°，得到△A''B''C''.   23．（12分）在某市举办的“读好书，讲礼仪”活动中，东华学校积极行动，各班图书角的新书、好书不断增多，除学校购买外，还有师生捐献的图书．下面是七年级（1）班全体同学捐献图书的情况统计图：请你根据以上统计图中的信息，解答下列问题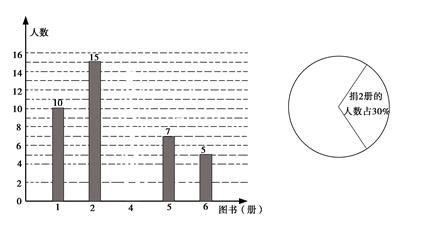：（1）该班有学生多少人？（2）补全条形统计图；（3）七（1）班全体同学所捐献图书的中位数和众数分别是多少？   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、B2、C3、C4、B5、D6、A7、B8、B9、B10、B11、B12、C 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、乙14、x＜2.15、-116、，        17、2 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）15，0.3；（2）图形见解析；（3）72；（4）300.19、（1）相等，理由见解析；（2）和；（3）存在，最大值为．20、（1）证明见解析；（2）.21、（1）平均数：260件；中位数：240件；众数：240件（2）不合理，定额为240较为合理22、（1）见解析；（2）见解析.23、（1）因为捐2本的人数是15人，占30％，所以该班人数为＝50（2）根据题意知，捐4本的人数为：50－(10＋15＋7＋5)＝1．(如图)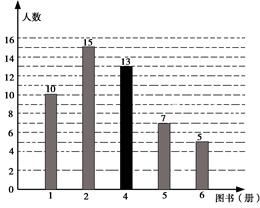（3）七（1）班全体同学所捐献图书的中位数是＝3(本)，众数是2本．