


2022-2023学年大同市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案
展开2022-2023学年大同市重点中学数学七年级第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
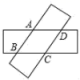
A.5 cm B.4.8 cm C.4.6 cm D.4 cm
2.如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
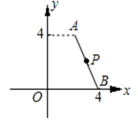
A.(3,2) B.(6,2) C.(6,4) D.(3,5)
3.如图,在矩形ABCD中对角线AC、BD相交于点O,∠ACB=60°,则∠AOB的大小为( )
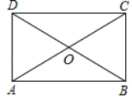
A.30° B.60° C.120° D.150°
4.已知![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.给出下列化简①(![]() )2=2:②
)2=2:②![]() 2;③
2;③![]() 12
12![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
A.①②③④ B.①②③ C.①② D.③④
6.如图所示的是一扇高为2m,宽为1.5m的长方形门框,光头强有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板最大的宽度为( )
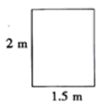
A.1.5m B.2m C.2.5m D.3m
7.某商品降价![]() 后欲恢复原价,则提价的百分数为( ).
后欲恢复原价,则提价的百分数为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列二次根式中,不能与![]() 合并的是( )
合并的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列四组线段中,可以构成直角三角形的是( )
A.4, 5, 6 B.5, 12, 13 C.2, 3, 4 D.1,![]() ,3
,3
10.下列各曲线中不能表示y是x函数的是( )
A.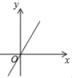 B.
B.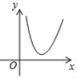 C.
C.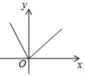 D.
D.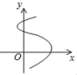
11.若a,b,c满足![]() 则关于x的方程
则关于x的方程![]() 的解是( )
的解是( )
A.1,0 B.-1,0 C.1,-1 D.无实数根
12.设三角形的三边长分别等于下列各组数,能构成直角三角形的是( )
A.![]() ,
, ![]() ,
,![]()
![]() B.
B.![]() ,
,![]() ,
,![]()
![]() C.
C.![]() ,
,![]() ,
,![]()
![]() D.4,5,6
D.4,5,6
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
14.函数![]() 的自变量
的自变量![]() 的取值范围是 .
的取值范围是 .
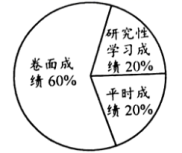
15.某校规定:学生的数学期未总计成须由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为![]() 分、
分、![]() 分、
分、![]() 分,则小明的数学期末总评成绩为________分.
分,则小明的数学期末总评成绩为________分.
16.如图,直线y=﹣![]() x+4
x+4![]() 分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
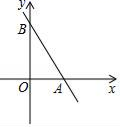
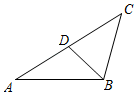
17.如图,已知△ABC∽△ADB,若AD=2,CD=2,则AB的长为_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
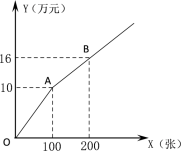
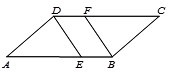
19.(5分)已知:如图,在□ABCD中,点E在AB上,点F在CD上,且DE∥BF.求证:DE = BF.
20.(8分)解不等式![]() ,并把解集表示在数轴上.
,并把解集表示在数轴上.
![]()
21.(10分)某河流防污治理工程已正式启动,由甲队单独做5个月后,乙队再加入合作3个月就可以完成这项工程。已知若甲队单独做需要10个月可以完成。
(1)乙队单独完成这项工程需要几个月?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
22.(10分)某校举办了一次趣味数学党赛,满分100分,学生得分均为整数,这次竞赛中,甲、乙两组学生成绩如下(单位:分)
甲组:30,60,60,60,60,60,70,90,90,100
乙组:50,60,60,60,70,70,70,70,80,90.
组别 | 平均分 | 中位数 | 方差 |
甲组 | 68 | a | 376 |
乙组 | b | 70 |
|
(1)以生成绩统计分析表中a=_________分,b=_________分.
(2)小亮同学说:“这次赛我得了70分,在我们小组中属中游略偏上!”双察上面表格判断,小亮可能是甲、乙哪个组的学生?并说明理由。
(3)计算乙组成的方差,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会进择哪一组?并说明理由。
23.(12分)某公司招聘一名员工,现有甲、乙两人竞聘,公司聘请了3位专家和4位群众代表组成评审组,评审组对两人竟聘演讲进行现场打分,记分采用100分制,其得分如下表:
评委(序号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙两位竞聘者得分的中位数分别是多少
(2)计算甲、乙两位应聘者平均得分,从平均得分看应该录用谁(结果保留一位小数)
(3)现知道1、2、3号评委为专家评委,4、5、6、7号评委为群众评委,如果对专家评委组与群众评委组的平均分数分别赋子适当的权,那么对专家评委组赋的权至少为多少时,甲的平均得分比乙的平均得分多0.5分及以上
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、B
3、C
4、B
5、C
6、C
7、C
8、C
9、B
10、D
11、C
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2
14、x>1
15、1
16、(2,﹣2![]() )或(6,2
)或(6,2![]() )
)
17、2![]() .
.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)![]() ;(2)甲、乙两单位购买门票分别为270张和130张.
;(2)甲、乙两单位购买门票分别为270张和130张.
19、证明见解析.
20、![]() ,数轴见解析.
,数轴见解析.
21、(1)15(2)方案一:甲队作4个月,乙队作9个月;方案二:甲队作2个月,乙队作1个月
22、(1)60,68;(2)小亮在甲组;(3)乙组的方差是116;乙组的方差小于甲组,选乙组同学代表学校参加复赛.
23、(1)甲得分中位数为:92(分),乙得分中位数为:91(分);(2)甲平均得分: 91(分),
乙平均得分: 91.6(分),平均得分看应该录用乙;(3)专家评委组赋的权至少为0.6时,甲的平均得分比乙的平均得分多0.5分及以上.
2023-2024学年抚州市重点中学数学八上期末学业质量监测模拟试题含答案: 这是一份2023-2024学年抚州市重点中学数学八上期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列各式中,正确的是,在平面直角坐标系中,点M,在下列运算中,正确的是等内容,欢迎下载使用。
2023-2024学年衡水市重点中学数学八上期末学业质量监测模拟试题含答案: 这是一份2023-2024学年衡水市重点中学数学八上期末学业质量监测模拟试题含答案,共7页。试卷主要包含了已知,如图所示,下列各数中,无理数的是等内容,欢迎下载使用。
2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,一次函数,当时,x的取值范围是,下列命题的逆命题正确的是,下列方程中有一根为3的是等内容,欢迎下载使用。













