2022-2023学年固原市重点中学七下数学期末考试模拟试题含答案

这是一份2022-2023学年固原市重点中学七下数学期末考试模拟试题含答案，共6页。
2022-2023学年固原市重点中学七下数学期末考试模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。2．答题时请按要求用笔。3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1．某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛，在选拔比赛中，每人射击10次，他们10次成绩的平均数及方差如下表所示： 甲乙丙丁平均数/环方差/环请你根据表中数据选一人参加比赛，最合适的人选是（    ）A．甲 B．乙 C．丙 D．丁2．点A，B，C，D在数轴上的位置如图所示，则实数对应的点可能是　　A．点A B．点B C．点C D．点D3．点在平面直角坐标系的（   ）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．关于的方程的解是正数，则的取值范围是（    ）A． B． C． D．5．10名学生的平均成绩是x，如果另外5名学生每人得90分，那么整个组的平均成绩是（　　）A． B． C． D．6．若直线经过点，直线经过点，且与关于轴对称，则与的交点坐标为（    ）A． B． C． D．7．如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为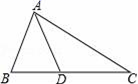（　　）A．35° B．40° C．45° D．50°8．使下列式子有意义的实数x的取值都满足的式子的是（    ）A． B． C． D．9．如图，在正方形中，为边上一点，将沿折叠至处， 与交于点，若，则的大小为（    ）A． B． C． D．10．如图，四边形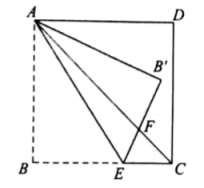ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=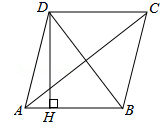（    ）A． B． C．12 D．24二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，在平行四边形ABCD中，AB＝2AD，BE平分∠ABC交CD于点E，作BF⊥AD，垂足为F，连接EF，小明得到三个结论：①∠FBC＝90°；②ED＝EB；③S△EBF＝S△EDF+S△EBC；则三个结论中一定成立的是_____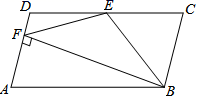．12．公路全长为skm，骑自行车t小时可到达，为了提前半小时到达，骑自行车每小时应多走_____________.13．如图 ，D 为△ABC 的 AC 边上的一点，∠A＝∠DBC＝36°，∠C＝72°，则图中 共有等腰三角形____个.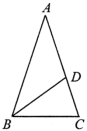14．将直线y＝2x＋1向下平移3个单位长度后所得直线的表达式是  ______．15．如图，平行四边形ABCD中，AB：BC＝3：2，∠DAB＝60°，E在AB上，如果AE：EB＝1：2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，那么DP：DC等于_____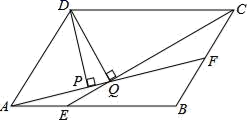．16．某老师为了解学生周末学习时间的情况，在所任班级中随机调查了10名学生，绘成如图所示的条形统计图，则这10名学生周末学习的平均时间是_______小时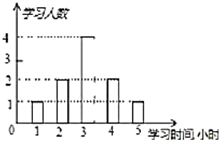．三、解下列各题(本大题共8小题，共72分)17．（8分）先化简(1+)÷，再选择一个恰当的x值代人并求值．   18．（8分）如图，在△ABC中，BD、CE分别为AC、AB边上的中线，BD、CE交于点H，点G、F分别为HC、HB的中点，连接AH、DE、EF、FG、GD，其中HA＝BC．（1）证明：四边形DEFG为菱形；（2）猜想当AC、AB满足怎样的数量关系时，四边形DEFG为正方形，并说明理由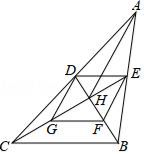．   19．（8分）如图，四边形 ABCD 为平行四边形，AD＝a，BE∥AC，DE 交AC的延长线于F点，交BE于E点． （1）求证：DF＝FE ； （2）若 AC＝2CF，∠ADC＝60°，AC⊥DC，求BE的长； （3）在（2）的条件下，求四边形ABED的面积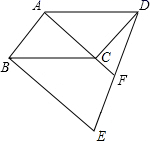．    20．（8分）已知关于x、y的方程组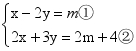的解满足不等式组.求满足条件的m的整数值.   21．（8分）如图，在▱ABCD中，对角线AC、BD相交于点O，且OA=OB（1）求证：四边形ABCD是矩形；（2）若AB=5，∠AOB=60°，求BC的长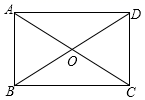．   22．（10分）如果一个多位自然数的任意两个相邻数位上，右边数位上的数总比左边数位上的数大1，则我们称这样的自然数叫“美数”，例如：123，3456，67，…都是“美数”．（1）若某个三位“美数”恰好等于其个位的76倍，这个“美数”为　   　．（2）证明：任意一个四位“美数”减去任意一个两位“美数”之差再减去1得到的结果定能被11整除；（3）如果一个多位自然数的任意两个相邻数位上，左边数位上的数总比右边数位上的数大1，则我们称这样的自然数叫“妙数”，若任意一个十位为为整数）的两位“妙数”和任意一个个位为为整数）的两位“美数”之和为55，则称两位数为“美妙数”，并把这个“美妙数”记为，则求的最大值．   23．（10分）如图，在△ABC中，AB＝AC，AD平分∠BAC交BC于点D，在线段AD上任到一点P（点A除外），过点P作EF∥AB，分别交AC、BC于点E、F，作PQ∥AC，交AB于点Q，连接QE与AD相交于点G．（1）求证：四边形AQPE是菱形．（2）四边形EQBF是平行四边形吗？若是，请证明；若不是，请说明理由．（3）直接写出P点在EF的何处位置时，菱形AQPE的面积为四边形EQBF面积的一半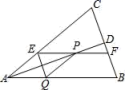．   24．（12分）已知一次函数的图象经过点（-2，-7）和（2，5），求该一次函数解析式并求出函数图象与y轴的交点坐标.   参考答案 一、选择题(每小题3分,共30分)1、A2、B3、D4、D5、D6、D7、A8、D9、B10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、①③12、－13、114、y＝1x－115、16、3 三、解下列各题(本大题共8小题，共72分)17、x+1     当x=2时，原式=318、（1）证明见解析；（2）当AC＝AB时，四边形DEFG为正方形，证明见解析19、（1）证明见解析（2） （3） 20、－3，－1.21、（1）证明见解析；（2）22、 (1)456 （2）见解析 （3）4223、（1）见解析；（2）结论：四边形EQBF是平行四边形．见解析；（3）当P为EF中点时，S菱形AEPQ＝S四边形EFBQ.24、y=3x-1, 函数图象与y轴的交点坐标(0,-1).