2022-2023学年天津市宁河县名校数学七下期末学业水平测试试题含答案

这是一份2022-2023学年天津市宁河县名校数学七下期末学业水平测试试题含答案，共7页。
2022-2023学年天津市宁河县名校数学七下期末学业水平测试试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题(每小题3分,共30分)1．关于频率与概率有下列几种说法：①“明天下雨的概率是90%”表示明天下雨的可能性很大；②“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上；③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖；④“抛一枚硬币正面朝上的概率为”表示随着抛掷次数的增加，“抛出正面朝上”这一事件发生的频率稳定在附近，正确的说法是（    ）A．②④ B．②③ C．①④ D．①③2．下列代数式属于分式的是（    ）A． B． C． D．3．已知 x＝－1 是一元二次方程 x2＋px＋q＝0 的一个根，则代数式 p－q 的值是（    ）A．1 B．－1 C．2 D．－24．如图，把两块全等的的直角三角板、重叠在一起，，中点为，斜边中点为，固定不动，然后把围绕下面哪个点旋转一定角度可以使得旋转后的三角形与原三角形正好合成一个矩形（三角板厚度不计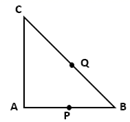）（    ）A．顶点 B．顶点 C．中点 D．中点5．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD+PE的和最小值为(　　)A． B．4 C．3 D．6．在函数中，自变量必须满足的条件是（    ）A． B． C． D．7．反比例函数的图象的一支在第二象限，则的取值范围是（）A． B． C． D．8．下列各数中，能使不等式x﹣3＞0成立的是(　　)A．﹣3 B．5 C．3 D．29．2022年将在北京﹣张家口举办冬季奥运会，很多学校开设了相关的课程．某校8名同学参加了冰壶选修课，他们被分成甲、乙两组进行训练，身高（单位：cm）如下表所示： 队员1队员2队员3队员4甲组176177175176乙组178175177174设两队队员身高的平均数依次为，，方差依次为S甲2，S乙2，下列关系中完全正确的是（　　）A．＝，S甲2＜S乙2 B．＝，S甲2＞S乙2C．＜，S甲2＜S乙2 D．＞，S甲2＞S乙210．在下述命题中,真命题有（   ）（1）对角线互相垂直的四边形是菱形；（2）三个角的度数之比为的三角形是直角三角形；（3）对角互补的平行四边形是矩形；（4）三边之比为的三角形是直角三角形..A．个 B．个 C．个 D．个二、填空题(本大题共有6小题，每小题3分，共18分)11．若一个等腰三角形的顶角等于70°,则它的底角等于________度，12．一组数2、a、4、6、8的平均数是5，这组数的中位数是______．13．与最简二次根式是同类二次根式，则__________．14．在平面直角坐标系中，点P（-3,2）关于x轴对称的点P1的坐标是______________.15．计算：的结果是_____．16．将一个有80个数据的一组数分成四组，绘出频数分布直方图，已知各小长方形的高的比为，则第二小组的频数为______.三、解下列各题(本大题共8小题，共72分)17．（8分）计算(2+1)(2﹣1)﹣(1﹣2)2   18．（8分）计算   19．（8分）已知关于x的方程2x2+kx-1=0. (1)求证：方程有两个不相等的实数根．(2)若方程的一个根是-1，求方程的另一个根．   20．（8分）已知：在平面直角坐标系中，边长为8的正方形OABC的两边在坐标轴上（如图）．（1）求点A，B，C的坐标．（2）经过A，C两点的直线l上有一点P，点D（0，6）在y轴正半轴上，连PD，PB（如图1），若PB2﹣PD2＝24，求四边形PBCD的面积．（3）若点E（0，1），点N（2，0）（如图2），经过（2）问中的点P有一条平行于y轴的直线m，在直线m上是否存在一点M，使得△MNE为直角三角形？若存在，求M点的坐标；若不存在，请说明理由．   21．（8分）在太空种子种植体验实践活动中，为了解“宇番2号”番茄，某校科技小组随机调查60株番茄的挂果数量x（单位：个），并绘制如下不完整的统计图表：“宇番2号”番茄挂果数量统计表挂果数量x（个）
 频数（株）
 频率
 25≤x＜35
 6
 0.1
 35≤x＜45
 12
 0.2
 45≤x＜55
 a
 0.25
 55≤x＜65
 18
 b
 65≤x＜75
 9
 0.15
 请结合图表中的信息解答下列问题：（1）统计表中，a=     ，b=     ；（2）将频数分布直方图补充完整；（3）若绘制“番茄挂果数量扇形统计图”，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为     °；（4）若所种植的“宇番2号”番茄有1000株，则可以估计挂果数量在“55≤x＜65”范围的番茄有     株．   22．（10分）我县某中学开展“庆十一”爱国知识竞赛活动，九年级（1）、（2）班各选出名选手参加比赛，两个班选出的名选手的比赛成绩（满分为100分）如图所示。（1）根据图示填写如表：班级中位数（分）众数（分）九（1）                  85九（2）80                   （2）请你计算九（1）和九（2）班的平均成绩各是多少分。（3）结合两班竞赛成绩的平均数和中位数，分析哪个班级的竞赛成绩较好（4）请计算九（1）、九（2）班的竞赛成绩的方差，并说明哪个班的成绩比较稳定？   23．（10分）计算：；．海伦公式是利用三角形三条边长求三角形面积的公式，用符号表示为：其中a，b，c为三角形的三边长，，S为三角形的面积利用海伦公式求，，时的三角形面积S．   24．（12分）以四边形ABCD的边AB，AD为边分别向外侧作等边△ABF和等边△ADE，连接EB，FD，交点为G.(1)当四边形ABCD为正方形时(如图1)，EB和FD的数量关系是         ；(2)当四边形ABCD为矩形时(如图2)，EB和FD具有怎样的数量关系？请加以证明；(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由．   参考答案 一、选择题(每小题3分,共30分)1、C2、A3、A4、D5、B6、B7、A8、B9、A10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、513、114、（-3，-2）15、116、2 三、解下列各题(本大题共8小题，共72分)17、4－2.18、 (1)；(2)1.19、 (1)证明见解析；(2).20、（1）A(8,0),B(8,8),C(0,8)；（2）15；（3）M的坐标是(3,7)或(3,2)21、（1）15，0.3；（2）图形见解析；（3）72；（4）300.22、（1）；（2）甲：85，乙：85；（3）九（1）班成绩较好；（4）九（1）班成绩比较稳定．23、 (1) ①5; ②5;(2) ,3.24、（1）EB=FD；（2）EB=FD，证明见解析；（3）∠EGD不发生变化．