


2022-2023学年安徽省六安市皋城中学数学七年级第二学期期末统考试题含答案
展开这是一份2022-2023学年安徽省六安市皋城中学数学七年级第二学期期末统考试题含答案,共7页。
2022-2023学年安徽省六安市皋城中学数学七年级第二学期期末统考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.如图,矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积s是动点P运动的路径总长x的函数,这个函数的大致图象可能是
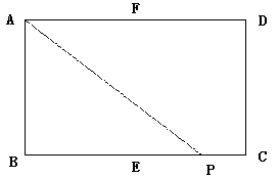
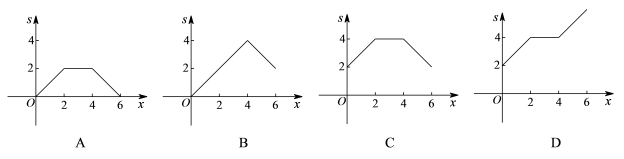
A.A B.B C.C D.D
2.用配方法解一元二次方程x2-8x+2=0,此方程可化为的正确形式是( ).
A.(x-4)2=14 B.(x-4)2=18 C.(x+4)2=14 D.(x+4)2=18
3.如图,在Rt△ABC中,AC=6,BC=8,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( )
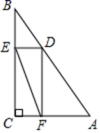
A.6 B.![]() C.5 D.
C.5 D.![]()
4.把分式![]() 中
中![]() 、
、![]() 的值都扩大为原来的2倍,分式的值( )
的值都扩大为原来的2倍,分式的值( )
A.缩小为原来的一半 B.扩大为原来的2倍
C.扩大为原来的4倍 D.不变
5.用配方法解一元二次方程![]() ,下列配方正确的是( )
,下列配方正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )
A.(x+3)2=1 B.(x﹣3)2=1
C.(x+3)2=19 D.(x﹣3)2=19
7.已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,则点
轴对称,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如果把分式![]() 中的x和y都扩大为原来的2倍,那么分式的值( )
中的x和y都扩大为原来的2倍,那么分式的值( )
A.不变 B.缩小2倍 C.扩大2倍 D.扩大4倍
9.函数![]() 自变量
自变量![]() 的值可以是( )
的值可以是( )
A.-1 B.0 C.1 D.2
10.如图,在平面直角坐标系中,点A、B的坐标分别是(4,0)、(0,3),点O'在直线y=2x(x≥0)上,将△AOB沿射线OO'方向平移后得到△A'O'B’.若点O'的横坐标为2,则点A'的坐标为( )
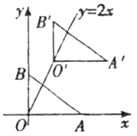
A.(4,4) B.(5,4) C.(6,4) D.(7,4)
二、填空题(本大题共有6小题,每小题3分,共18分)
11.分式![]() 与
与![]() 的最简公分母是_____.
的最简公分母是_____.
12.若![]() ,则
,则![]() _______
_______![]() (填不等号).
(填不等号).
13.在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程![]() 的两个实数根,则△ABC的周长为__________.
的两个实数根,则△ABC的周长为__________.
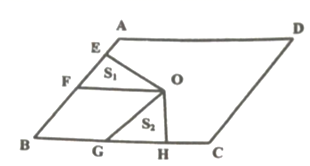
14.如图,点![]() 是平行四边形
是平行四边形![]() 的对角线交点,
的对角线交点,![]() ,
,![]() 是
是![]() 边上的点,且
边上的点,且![]() ;
;![]() 是
是![]() 边上的点,且
边上的点,且![]() ,若
,若![]() 分别表示
分别表示![]() 和
和![]() 的面积,则
的面积,则![]() __________.
__________.
15.将函数![]() 的图象向上平移3个单位长度,得到的函数图象的解析式为______.
的图象向上平移3个单位长度,得到的函数图象的解析式为______.
16.若y=![]() ,则x+y= .
,则x+y= .
三、解下列各题(本大题共8小题,共72分)
17.(8分)在2019年春季环境整治活动中,某社区计划对面积为![]() 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为
的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用5天.
区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成绿化任务,求
天,刚好完成绿化任务,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
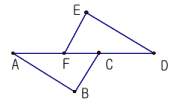
18.(8分)如图,已知 BC∥EF,BC=EF,AF=DC.试证明:AB=DE.
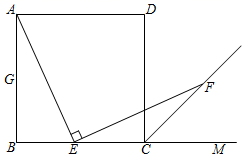
19.(8分)如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.
20.(8分)在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
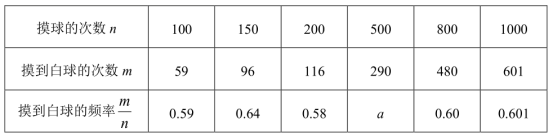
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
21.(8分)解方程:![]() +
+![]() =1.
=1.
22.(10分)为了解初二学生参加户外活动的情况,某县教育局对其中500名初二学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如下统计图。(参加户外活动的时间分为四种类别:“0.5小时”,“1小时”,“1.5小时”,“2小时”)
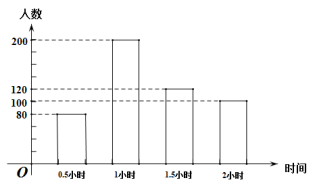
请根据图示,回答下列问题:
(1)求学生每天户外活动时间的平均数,众数和中位数;
(2)该县共有12000名初二学生,请估计该县每天户外活动时间超过1小时的初二学生有多少人?
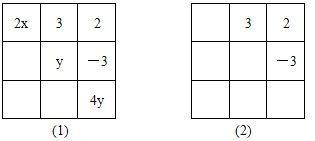
23.(10分)如图,在3×3的方格内,填写了一些代数式和数.
(1)在图(1)中各行、各列及对角线上三个数之和都相等,请你求出x,y的值;
(2)把满足(1)的其它6个数填入图(2)中的方格内.
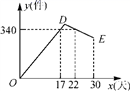
24.(12分)某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、D
4、D
5、A
6、D
7、B
8、C
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2a-2b
12、<
13、9或10.1
14、3:1
15、![]()
16、1.
三、解下列各题(本大题共8小题,共72分)
17、(1)甲、乙两工程队每天能完成绿化面积分别为![]() 和
和![]() ;(2)
;(2)![]() ;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
18、证明见解析
19、(1)见解析;(2)成立,理由见解析;(3)∠AEF=90°不发生变化.理由见解析.
20、 (1) 0.58;(2) 0.6;(3)白球12(个),黑球8 (个)
21、![]()
22、(1)平均数是1.24;众数:1;中位数:1;(2)该校每天户外活动时间超过1小时的学生有5280人.
23、 (1)x=-1,y=1;(2)见解析.
24、 (1)330;660 (2)答案见解析(3) 日销售利润不低于640元的天数共有11天,试销售期间,日销售最大利润是720元.
相关试卷
这是一份2023-2024学年安徽省六安市皋城中学数学九上期末统考试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,若是方程的根,则的值为,如图,已知,且,则等内容,欢迎下载使用。
这是一份2023-2024学年安徽省六安市皋城中学数学八年级第一学期期末调研试题含答案,共6页。试卷主要包含了若有意义,则x的取值范围是,下列命题中是假命题的是,命题“邻补角的和为”的条件是,点A、B都在直线y=kx+2等内容,欢迎下载使用。
这是一份安徽省六安市皋城中学2022-2023学年七年级数学第二学期期末联考模拟试题含答案,共6页。试卷主要包含了一次函数的图象不经过,对于二次函数 y=等内容,欢迎下载使用。













