2022-2023学年山东威海市14中学数学七年级第二学期期末调研试题含答案

这是一份2022-2023学年山东威海市14中学数学七年级第二学期期末调研试题含答案，共6页。
2022-2023学年山东威海市14中学数学七年级第二学期期末调研试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。2．答题时请按要求用笔。3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1．在四边形ABCD中，∠A，∠B，∠C，∠D度数之比为1：2：3：3，则∠B的度数为（    ）A．30°    B．40°    C．80°    D．120°2．在ABCD中，∠A：∠B：∠C：∠D的值可以是（  ）A．1：2：3：4 B．3：4：4：3 C．3：3：4：4 D．3：4：3：43．若分式有意义，则的取值范围是（  ）A． B． C． D．4．如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是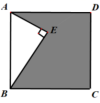（  ）A．12 B．16 C．19 D．255．已知函数y=，则自变量x的取值范围是（　　）A．﹣1＜x＜1 B．x≥﹣1且x≠1 C．x≥﹣1 D．x≠16．如图所示，在中，，、是斜边上的两点，且，将绕点按顺时针方向旋转后得到，连接．有下列结论：①；②；③；④其中正确的有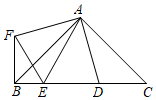（    ）A．①②③④ B．②③ C．②③④ D．②④7．如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE，下列结论：①∠CAD＝30°；②SABCD＝AB•AC；③OB＝AB：④OE＝BC．其中成立的有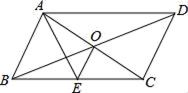（　　）A．①②③ B．①②④ C．①③④ D．②③④8．中国传统扇文化有着深厚的底蕴，下列扇面图形是中心对称图形的是(    )A． B． C． D．9．不等式组的解集是（    ）A． B． C． D．10．如图，在中，是上一点，，，垂足为，是的中点，若，则的长度为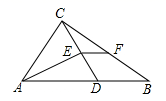（    ）A．36 B．18 C．9 D．5二、填空题(本大题共有6小题，每小题3分，共18分)11．一组数据：3，5，9，12，6的极差是_________．12．在平面直角坐标系中，一次函数的图象与轴的交点坐标为__________．13．公路全长为skm，骑自行车t小时可到达，为了提前半小时到达，骑自行车每小时应多走_____________.14．如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB方向平移得到△DEF，若四边形ABED的面积等于8，则平移的距离为_____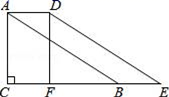．15．如图，OP=1，过P作PP1⊥OP且PP1=1，得OP1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥OP2且P2P3=１，得OP3=2…依此法继续作下去，得=____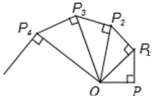．16．如图，于，于，且，，，则_______．三、解下列各题(本大题共8小题，共72分)17．（8分）某校八年级师生为了响应“绿水青山就是金山银山”的号召，在今年3月的植树月活动中到某荒山植树，如图是抽查了其中20名师生植树棵数的统计图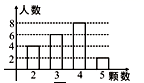．（1）求这20名师生种树棵数的平均数、众数、中位数；（2）如果该校八年级共有师生500名，所植树的存活率是90%，估计所植的树共有多少棵存活？   18．（8分）一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.（1）若降价3元，则平均每天销售数量为________件；    （2）当每件商品降价多少元时，该商店每天销售利润为1200元？   19．（8分）如图，中，是上的一点，若，，，，求的面积．   20．（8分）某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售，当此农产品售价为每袋36元时，3月份销售125袋，4、5月份该农产品十分畅销，销售量持续走高.在售价不变的基础上，5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.（1）求4、5这两个月销售量的月平均增长率；（2）6月份起，该商店采用降价促销的方式回馈顾客，经调查发现，该农产品每降价1元/袋，销量就增加4袋，当农产品每袋降价多少元时，该商店6月份获利1920元？   21．（8分）化简：(.   22．（10分）如图，已知直线与直线相交于点. 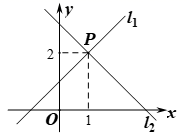（1）求、的值；（2）请结合图象直接写出不等式的解集.   23．（10分） “西瓜足解渴，割裂青瑶肤”，西瓜为夏季之水果，果肉味甜，能降温去暑；种子含油，可作消遣食品；果皮药用，有清热、利尿、降血压之效.某西瓜批发商打算购进“黑美人”西瓜与“无籽”西瓜两个品种的西瓜共70000千克．（1）若购进“黑美人”西瓜的重量不超过“无籽”西瓜重量的倍，求“黑美人”西瓜最多购进多少千克？（2）该批发商按（1）中“黑美人”西瓜最多重量购进，预计“黑美人”西瓜售价为4元/千克；“无籽”西瓜售价为5元/千克，两种西瓜全部售完.由于存储条件的影响，“黑美人”西瓜与“无籽”西瓜分别有与的损坏而不能售出.天气逐渐炎热，西瓜热卖，“黑美人”西瓜的销售价格上涨，“无籽”西瓜的销售价格上涨，结果售完之后所得的总销售额比原计划下降了3000元，求的值．   24．（12分）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连接这四个点，得四边形EFGH．（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），①试用含α的代数式表示∠HAE；②求证：HE=HG；③四边形EFGH是什么四边形？并说明理由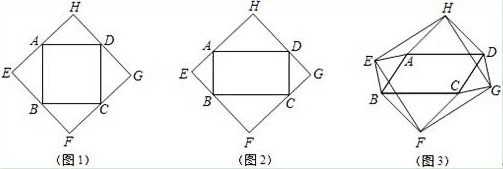．   参考答案 一、选择题(每小题3分,共30分)1、C2、D3、A4、C5、B6、C7、B8、C9、A10、C 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、13、－14、115、16、140° 三、解下列各题(本大题共8小题，共72分)17、（1）平均数是3.4棵，众数是4棵，中位数是3.5棵；（2）1．18、（1）26；（2）每件商品降价2元时，该商店每天销售利润为12元.19、的面积是．20、（1）4、5两个月销售量的平均增长率为20%；（2）每袋降价3元时，获利1920元.21、8-422、（1），；（2）.23、（1）最多（2）24、 (1) 四边形EFGH的形状是正方形;(2)①∠HAE=90°+a;②见解析；③四边形EFGH是正方形，理由见解析