


2022-2023学年山东省临沂市数学七年级第二学期期末质量跟踪监视模拟试题含答案
展开这是一份2022-2023学年山东省临沂市数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
2022-2023学年山东省临沂市数学七年级第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果一次函数y=kx+b(k、b是常数)的图象不经过第二象限,那么k、b应满足的条件是( )
A.k>0,且b≤0 B.k<0,且b>0 C.k>0,且b≥0 D.k<0,且b<0
2.如图,点A在双曲线![]() 上,点B在双曲线
上,点B在双曲线![]() 上,且AB∥y轴,C、D在y轴上,若四边形ABCD为矩形,则它的面积为( )
上,且AB∥y轴,C、D在y轴上,若四边形ABCD为矩形,则它的面积为( )

A.1.5 B.1 C.3 D.2
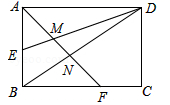
3.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如果a为任意实数, 下列各式中一定有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
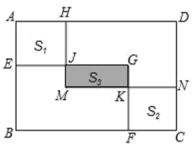
5.如果,在矩形![]() 中,矩形
中,矩形![]() 通过平移变换得到矩形
通过平移变换得到矩形![]() ,点
,点![]() 都在矩形
都在矩形![]() 的边上,若
的边上,若![]() ,且四边形
,且四边形![]() 和
和![]() 都是正方形,则图中阴影部分
都是正方形,则图中阴影部分![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在二次根式![]() 中,a能取到的最小值为( )
中,a能取到的最小值为( )
A.0 B.1 C.2 D.2.5
7.如图,正方形![]() 的边长为2,点
的边长为2,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() .连接CF,则
.连接CF,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,四边形ABCD是正方形,点E、F分别在AD、CD上,AF、BE相交于点G,且AF=BE,则下列结论不正确的是:( )
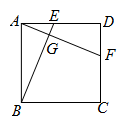
A.AF⊥BE B.BG=GF C.AE=DF D.∠EBC=∠AFD
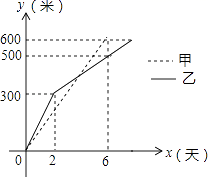
9.我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
A.1 ![]() B.2
B.2 ![]() C.3
C.3 ![]() D.4
D.4
10.顺次连接一个四边形的各边中点,得到了一个正方形,这个四边形最可能是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
11.下列语句正确的是( )
A.![]() 的平方根是6 B.负数有一个平方根
的平方根是6 B.负数有一个平方根
C.![]() 的立方根是
的立方根是![]() D.8的立方根是2
D.8的立方根是2
12.定义![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() <
<![]() 时,
时,![]() ;已知函数
;已知函数![]() ,则该函数的最大值是
,则该函数的最大值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.若式子![]() 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .
14.任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
15.若方程组![]() 的解是
的解是![]() ,那么|a-b|= ______________.
,那么|a-b|= ______________.
16.化简:![]() ______.
______.
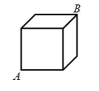
17.如图是棱长为4cm的立方体木块,一只蚂蚁现在A点,若在B点处有一块糖,它想尽快吃到这块糖,则蚂蚁沿正方体表面爬行的最短路程是______cm.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
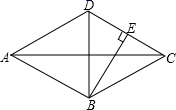
18.(5分)已知:菱形ABCD中,对角线![]() 于点E,求菱形ABCD的面积和BE的长.
于点E,求菱形ABCD的面积和BE的长.
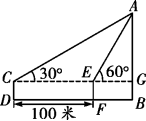
19.(5分)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米到达F处,又测得电视塔顶端A的仰角为60°,求这个电视塔的高度AB.(参考数据![]() ).
).
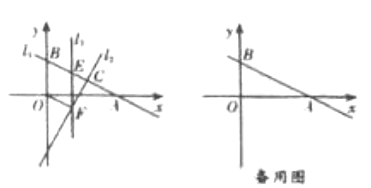
20.(8分)如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.
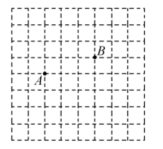
21.(10分)本题有许多画法,你不妨试一试:如图所示的是![]() 8的正方形网格,A、B两点均在格点上,现请你在下图中分别画出一个以A、B、C、D为顶点的菱形(可包含正方形),要求:(1)C、D也在格点上;(2)只能使用无刻度的直尺;(3)所画的三个菱形互不全等。
8的正方形网格,A、B两点均在格点上,现请你在下图中分别画出一个以A、B、C、D为顶点的菱形(可包含正方形),要求:(1)C、D也在格点上;(2)只能使用无刻度的直尺;(3)所画的三个菱形互不全等。


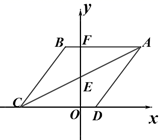
22.(10分)如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
23.(12分)某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、
、![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、D
3、B
4、C
5、A
6、C
7、D
8、B
9、D
10、A
11、D
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]() .
.
14、2
15、1
16、![]()
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、菱形ABCD的面积为![]() 的长为
的长为![]() .
.
19、87.6米
20、(1)(8,0) , (0,4) ;(2)当m为![]() 时,四边形OBEF是平行四边形.
时,四边形OBEF是平行四边形.
21、见解析
22、 (1)B(-1,4),C(-4,0);![]() 见解析;(3)
见解析;(3)![]() 或7.5.
或7.5.
23、:(1)![]() =91分,
=91分,![]() =92分,
=92分,![]() =91分;(2)乙将被录用.
=91分;(2)乙将被录用.
相关试卷
这是一份2023-2024学年山东省临沂市12中学数学八上期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了若四边形ABCD中,∠A等内容,欢迎下载使用。
这是一份山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。
这是一份2022-2023学年山东省禹城市七年级数学第二学期期末质量跟踪监视模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列各式成立的是,在实数范围内,下列判断正确的是等内容,欢迎下载使用。












