


2022-2023学年山东省利津县数学七年级第二学期期末学业水平测试模拟试题含答案
展开
这是一份2022-2023学年山东省利津县数学七年级第二学期期末学业水平测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若是关于,的二元一次方程,则等内容,欢迎下载使用。
2022-2023学年山东省利津县数学七年级第二学期期末学业水平测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④直角三角形的两个锐角互余;⑤同角或等角的补角相等.其中真命题的个数是( )A.2个 B.3个 C.4个 D.5个2.化简![]() 的结果是A.-2 B.2 C.-4 D.43.如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,①△ABE≌△DCE;②△ABE和△DCE都是等腰直角三角形;③AE=DE;④△BCE是等边三角形,以上结论正确的有( )
的结果是A.-2 B.2 C.-4 D.43.如图,长方形ABCD中,BE、CE分别平分∠ABC和∠DCB,点E在AD上,①△ABE≌△DCE;②△ABE和△DCE都是等腰直角三角形;③AE=DE;④△BCE是等边三角形,以上结论正确的有( )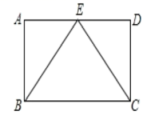 A.1个 B.2个 C.4个 D.3个4.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计.下列表示我国古代窗棂样式结构图案中,既是中心对称图形又是轴对称图形的是( )A.
A.1个 B.2个 C.4个 D.3个4.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计.下列表示我国古代窗棂样式结构图案中,既是中心对称图形又是轴对称图形的是( )A.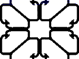 B.
B.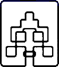 C.
C. D.
D. 5.如图,在四边形
5.如图,在四边形![]() 中,
中,![]() ,点
,点![]() 分别为线段
分别为线段![]() 上的动点(含端点,但点
上的动点(含端点,但点![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 长度的最大值为( )
长度的最大值为( )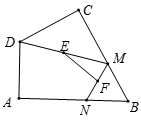 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.若
6.若![]() 是关于
是关于![]() ,
,![]() 的二元一次方程,则( )A.
的二元一次方程,则( )A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() 7.甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( )
7.甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市.已知货车出发1小时后客车再出发,先到终点的车辆原地休息.在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论错误的是( ) 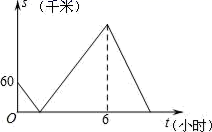 A.货车的速度是60千米/小时B.离开出发地后,两车第一次相遇时,距离出发地150千米C.货车从出发地到终点共用时7小时D.客车到达终点时,两车相距180千米8.下列由左到右的变形,属于因式分解的是( )A.
A.货车的速度是60千米/小时B.离开出发地后,两车第一次相遇时,距离出发地150千米C.货车从出发地到终点共用时7小时D.客车到达终点时,两车相距180千米8.下列由左到右的变形,属于因式分解的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图①,
9.如图①,![]() ,点
,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .如图②,以图①中的
.如图②,以图①中的![]() ,
,![]() 长为边建构矩形
长为边建构矩形![]() ,以
,以![]() 长为边建构正方形
长为边建构正方形![]() ,则矩形
,则矩形![]() 的面积为( )
的面积为( )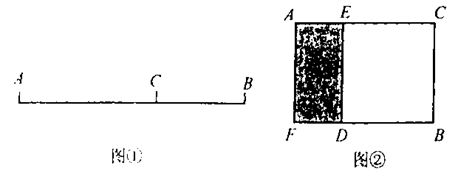 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.直线y=kx+b不经过第三象限,则k、b应满足( )A.k>0,b<0 B.k<0,b>0 C.k<0 b<0 D.k<0,b≥0二、填空题(本大题共有6小题,每小题3分,共18分)11.如果关于x的分式方程
10.直线y=kx+b不经过第三象限,则k、b应满足( )A.k>0,b<0 B.k<0,b>0 C.k<0 b<0 D.k<0,b≥0二、填空题(本大题共有6小题,每小题3分,共18分)11.如果关于x的分式方程![]() 有增根,则增根x的值为_____.12.关于x的方程
有增根,则增根x的值为_____.12.关于x的方程![]() =1的解是正数,则m的取值范围是________ .13.如图,已知
=1的解是正数,则m的取值范围是________ .13.如图,已知![]() 中,
中,![]() 边上的高
边上的高![]() ,则
,则![]() 的面积是______,
的面积是______,![]() 边上的高
边上的高![]() 的长是______.
的长是______.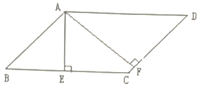 14.菱形ABCD的对角线
14.菱形ABCD的对角线![]() cm,
cm,![]() ,则其面积等于______.15.在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=
,则其面积等于______.15.在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=![]() 相交于点A,和双曲线y=
相交于点A,和双曲线y=![]() 交于点B,且AB=6,则点B的坐标是______.16.函数y=
交于点B,且AB=6,则点B的坐标是______.16.函数y=![]() 与y=k2x(k1,k2均是不为0的常数)的图象相交于A、B两点,若点A的坐标是(1,2),则点B的坐标是______.三、解下列各题(本大题共8小题,共72分)17.(8分)解方程(本题满分8分)(1)(x-5)2 =2(5-x)(2)2x2-4x-6=0(用配方法); 18.(8分)某市联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式.(2)月通话时间为多长时,A,B两种套餐收费一样?(3)什么情况下A套餐更省钱? 19.(8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=
与y=k2x(k1,k2均是不为0的常数)的图象相交于A、B两点,若点A的坐标是(1,2),则点B的坐标是______.三、解下列各题(本大题共8小题,共72分)17.(8分)解方程(本题满分8分)(1)(x-5)2 =2(5-x)(2)2x2-4x-6=0(用配方法); 18.(8分)某市联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式.(2)月通话时间为多长时,A,B两种套餐收费一样?(3)什么情况下A套餐更省钱? 19.(8分)如图,将平行四边形ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.
AD,连接CE,F是BC边的中点,连接FD.求证:四边形CEDF是平行四边形.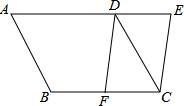 20.(8分)如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.
20.(8分)如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.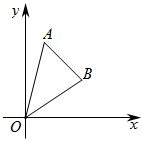 (1)求直线OB与AB的解析式;(2)求△AOB的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由. 21.(8分)某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.(1)求出y与m之间的函数关系式;(2)该商店如何进货才能获得最大利润?此时最大利润是多少元? 22.(10分)端午节放假期间,某学校计划租用
(1)求直线OB与AB的解析式;(2)求△AOB的面积.(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由. 21.(8分)某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.(1)求出y与m之间的函数关系式;(2)该商店如何进货才能获得最大利润?此时最大利润是多少元? 22.(10分)端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元. 甲种客车乙种客车载客量(人/辆)
元. 甲种客车乙种客车载客量(人/辆)![]()
![]() 租金(元/辆)
租金(元/辆)![]()
![]() (1)求出
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;(2)求出自变量的取值范围;(3)选择怎样的租车方案所需的费用最低?最低费用多少元? 23.(10分)计算:(1)
(辆)之间函数关系式;(2)求出自变量的取值范围;(3)选择怎样的租车方案所需的费用最低?最低费用多少元? 23.(10分)计算:(1)![]() (2)(
(2)(![]() )﹣(
)﹣(![]() ) 24.(12分)如图,在平面直角坐标系可中,直线y=x+1与y=﹣
) 24.(12分)如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.(1)求点A,B,C的坐标;(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.(1)求点A,B,C的坐标;(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;(3)当△CBD为等腰三角形时直接写出D坐标.
的值,不存在请说明理由;(3)当△CBD为等腰三角形时直接写出D坐标.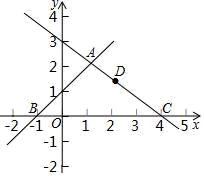 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、A5、B6、D7、C8、C9、C10、D. 二、填空题(本大题共有6小题,每小题3分,共18分)11、x=112、m<﹣2且m≠﹣113、12, 1. 14、
参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、A5、B6、D7、C8、C9、C10、D. 二、填空题(本大题共有6小题,每小题3分,共18分)11、x=112、m<﹣2且m≠﹣113、12, 1. 14、![]() 15、(3+
15、(3+![]() ,
,![]() )或(-3+
)或(-3+![]() ,
,![]() )16、 (-1,-2) 三、解下列各题(本大题共8小题,共72分)17、(1)x1=5,x2=3;(2)x1=3,x2=-1.18、 (1) y1=1.1x+15; y2=1.15x;(2)311;(3) 当月通话时间多于311分钟时,A套餐更省钱.19、见解析.20、(1)直线OB的解析式为
)16、 (-1,-2) 三、解下列各题(本大题共8小题,共72分)17、(1)x1=5,x2=3;(2)x1=3,x2=-1.18、 (1) y1=1.1x+15; y2=1.15x;(2)311;(3) 当月通话时间多于311分钟时,A套餐更省钱.19、见解析.20、(1)直线OB的解析式为![]() ,直线AB的解析式为y= -x+1(2)1;(3)①存在,(0,
,直线AB的解析式为y= -x+1(2)1;(3)①存在,(0,![]() );②存在,(2,-2)或(4,6)或(-2,2)21、(1)
);②存在,(2,-2)或(4,6)或(-2,2)21、(1)![]() =﹣200
=﹣200![]() +15000(20≤m<30);(2) 购进A型电动自行车20辆,购进B型10辆,最大利润是11000元.22、(1)
+15000(20≤m<30);(2) 购进A型电动自行车20辆,购进B型10辆,最大利润是11000元.22、(1)![]() ;(2)
;(2)![]() ,且
,且![]() 为整数;(3)租用甲种客车
为整数;(3)租用甲种客车![]() 辆,租用乙种客车
辆,租用乙种客车![]() 辆,所需的费用最低,最低费用
辆,所需的费用最低,最低费用![]() 元.23、(1)-1;(2)2
元.23、(1)-1;(2)2![]() +3
+3![]() .24、 (1)A(
.24、 (1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)点D的坐标为(﹣
;(3)点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
相关试卷
这是一份2023-2024学年山东省利津县九年级数学第一学期期末学业水平测试试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列图案中是中心对称图形的有等内容,欢迎下载使用。
这是一份山东省乐陵市2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案,共6页。试卷主要包含了若方程有增根,则a的值为,下列因式分解正确的是等内容,欢迎下载使用。
这是一份山东省广饶县2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,化简的结果是,计算的结果是,下列判断错误的是,关于x的一元二次方程等内容,欢迎下载使用。









