2022-2023学年北师大版七年级上学期数学期末试卷二+

这是一份2022-2023学年北师大版七年级上学期数学期末试卷二+，共13页。
0.4 D．
c
0.3
1 4
d
a
2
3
b
北师大版七年级数学期末试卷二
（上）

（本题共有10小题，满分30分）
一
、
1．
选择题
下列各数中，
每小题3分，

最小的一个数是．
（ ）

﹣3 B．0 D．
2
A．
﹣1 C．

携带2kg月球土壤顺利回到地球，往返超760000公里，
标
）
2．
12月17日凌晨，
．
嫦娥五号历时23天，

数据760000用科学记数法表示为回”三步走整体规划如期完成．
（
志着我国探月工程“绕、
落、

7.6×104 C．0.76×106
A．
76×104 B．
7.6×105 D．

2020年1月12日被世界卫生组织命名“2019﹣3．
新型冠状病毒，
因武汉病毒性肺炎病例而被发现，

我们可以看到这些病毒直径约为125纳米nCoV”．
（1纳米＝1×10﹣9米）
125纳米用科学记数法表示等于
冠状病毒是一个大型病毒家族，
，
（
借助电子显微镜，

）米．
1.25×10﹣10 B．1.25×10﹣7
A．
1.25×10﹣11 C．
1.25×10﹣8 D．

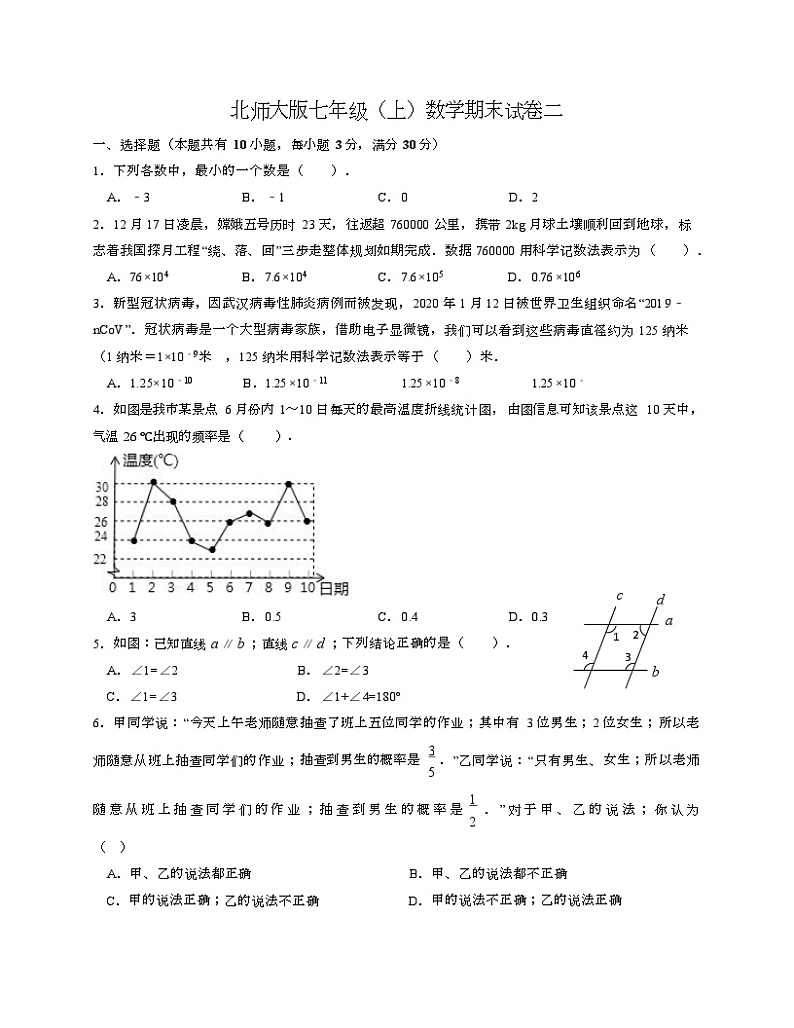
如图是我市某景点6月份内1～10日每天的最高温度折线统计图，由图信息可知该景点这10天中，
4．

气温26℃出现的频率是（ ）．












0.5 C．3 B．
A．

已知直线a ∥ b；下列结论正确的是
（ ）
5．
．
如图：
直线c ∥ d；

∠2=∠3A．
∠1=∠2 B．

∠1+∠4=180°C．
∠1=∠3 D．

甲同学说：“今天上午老师随意抽查了班上五位同学的作业；其中有3位男生；2位女生；所以老6．

”乙同学说：“只有男生、
抽查到男生的概率是 ．
女生；所以老师
3 5

师随意从班上抽查同学们的作业；

1
．
2
”对于甲、乙的说法；你认为

随意从班上抽查同学们的作业；抽查到男生的概率是

（ ）
乙的说法都正确 B．甲、
A．
甲、
乙的说法都不正确

乙的说法不正确 D．乙的说法正确
C．
甲的说法正确；
甲的说法不正确；

某数学学习小组为了解本校同学日常“垃圾分类”投放情况，其中A：
B：
C：
随机从本校同学中抽取部分同学进行调
每次分类投放，
经常分类投放，
7．

并将调查到的数据绘制成如图所示的扇形统计图，查，
从不分类投放，
有时分类投放，
D：

则下列说法中错误的是（ ）．

此次共随机调查了200名同学A．

选择“每次分类投放”垃圾的同学有55人B．
C．

选择“有时分类投放”垃圾所在扇形圆心角的度数为46.8°
选择“从不分类投放”垃圾的同学占比2%D．
8．

下列说法中正确的是A．
（ ）
．

两点之间，直线最短
B．
C．

由两条射线组成的图形叫做角
若过多边形的一个顶点可以画5条对角线，则这个多边形是八边形

则点C是线段AB的中点D．
9．
对于线段AC与BC，
某车间生产圆形铁片和长方形铁片，
若AC＝BC，

两个圆形铁片和一个长方形铁片可以制作成一个油桶，
（如图）

每个工人平均每小时可以生产圆形铁片120片或长方形铁片80片，已知该车间有工人42人，
为使生

设安排x人生产圆形铁片，．
产的铁片恰好配套，
可列方程（ ）

80x＝2×120（42﹣x） B．2×80x＝120（42﹣x）
A．

120x＝2×80C．
2×120x＝80
（42﹣x） D．
（42﹣x）

表4分别是从表1中截取的一部分，寻找规律，
表2、
表3、
其中m为整数且m
10．
如图，
观察表1，

则a+b+c＝．
（ ）
＞1，












m2﹣m+44 B．m2+m+44
A．
m2+m+46 C．
m2﹣m+46 D．

（本大题共8小题，,满分24分）
二、


11．
12．
填空题
计算：
每小题3分，


(x2) =3
．

甲醛是目前新装修房屋的主要空气污染物；长期接触对人体非常有害；
中华人民共和国国家标准

《居室空气中甲醛的卫生标准》规定：室内空气中甲醛的最高允许浓度是每立方米0.00008克；数据

0.00008用科学记数法可表示为 ．
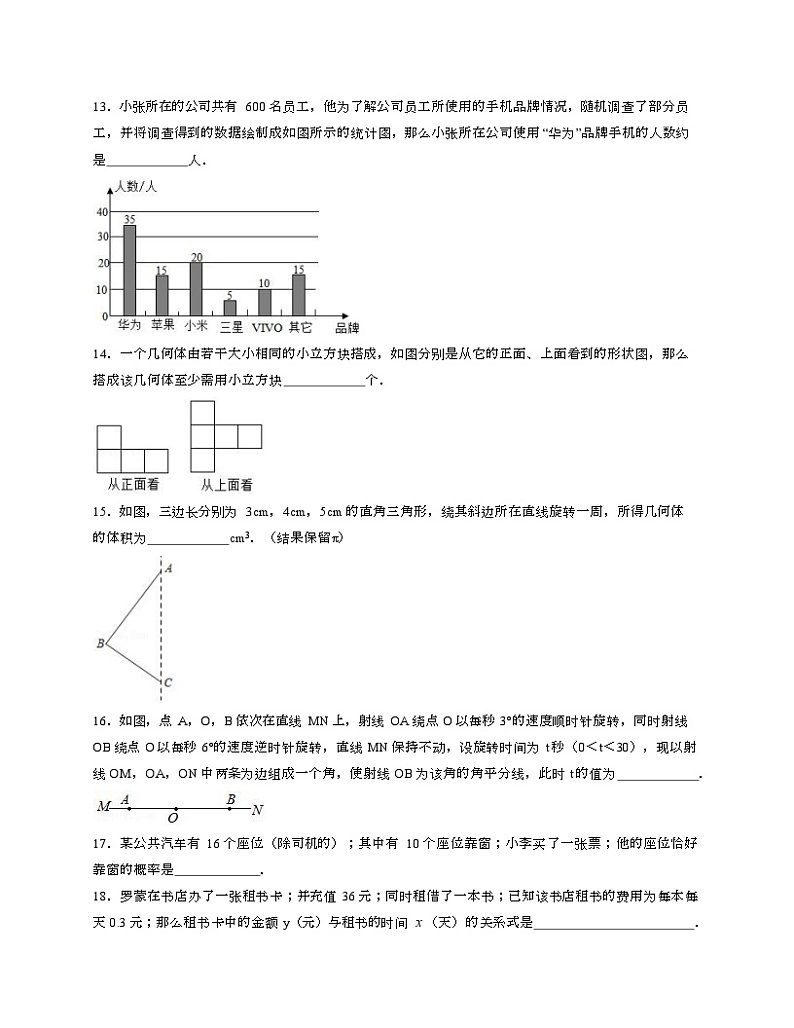
13．小张所在的公司共有600名员工，他为了解公司员工所使用的手机品牌情况，随机调查了部分员
工，并将调查得到的数据绘制成如图所示的统计图，那么小张所在公司使用“华为”品牌手机的人数约
是 人．












14．一个几何体由若干大小相同的小立方块搭成，如图分别是从它的正面、上面看到的形状图，那么
搭成该几何体至少需用小立方块 个．








15．如图，三边长分别为3cm，4cm，5cm的直角三角形，绕其斜边所在直线旋转一周，所得几何体
的体积为 cm3．（结果保留π）











16．如图，点A，O，B依次在直线MN上，射线OA绕点O以每秒3°的速度顺时针旋转，同时射线
OB绕点O以每秒6°的速度逆时针旋转，直线MN保持不动，设旋转时间为t秒（0＜t＜30），现以射
线OM，OA，ON中两条为边组成一个角，使射线OB为该角的角平分线，此时t的值为 ．



17．某公共汽车有16个座位（除司机的）；其中有10个座位靠窗；小李买了一张票；他的座位恰好
靠窗的概率是 ．
18．罗蒙在书店办了一张租书卡；并充值36元；同时租借了一本书；已知该书店租书的费用为每本每
天0.3元；那么租书卡中的金额y（元）与租书的时间x（天）的关系式是 ．
×
（1）











（2）
（ ﹣ ）
（﹣12）
﹣12020+（﹣2）4×
（共2小题，三、

19．
计算题
满分12分）


（6分）计算


﹣|﹣2+5|÷（1﹣ ）；












（﹣ ）+（﹣9）÷（﹣1）．












（﹣a2）3﹣a2•a4+（﹣2a4）2÷a2；20．
（6分）
（1）计算：












[(x - 3y) - (x - y)(x + y)]÷ (- 2y)（2）先化简，
y =-3
2
其中 x =2；
再求值：

（共4小题，四、
解答题
满分34分）

（6分）有9张卡片；分别写有1～9这九个数字；将它们背面朝上洗匀后；小明从中任意抽出一21．

；以卡片上的数字为十位上的数字；小芳从剩余的卡片中任意抽出一张；张（不放回）
以卡片上的数

字为个位上的数字；这个两位数为奇数；
小芳获胜．
（1）现小明已经摸到的数字为4；
这个两位数为偶数；
小明获胜；

那么小明获胜的概率是多少？小芳获胜的概率又是多少？






（2）现小明已经摸到的数字为5；

那么小明获胜的概率是多少？小芳获胜的概率又是多少？






（6分）
某校为防疫需要，
22．

实行错时错峰测温并开通专用通道上学，八年级人数如下表
该校七、

所示：
人数（人）

620

450

年级

七年级

八年级
①八年级学生进校时同时开通了A、八年级全部学生进校，
已知A通道每分
B两通道，
经过6分钟，

钟通过的人数是B通道每分钟通过人数的2倍．求A、
B通道每分钟通过的人数各是多少人？









学校决定在A通道旁边增开C通道，为节约学生进校时间，
在B通
②考虑到七年级人数更多的原因，

已知C通道每分钟通过的人数比A通道每分钟通过的人数多20%，道旁边增开D通道，
D通道每分钟

通过的人数比B通道每分钟通过的人数少20%，求七年级全部学生进校所需时间是多少分钟？

23．（10分）已知有理数a，b，c在数轴上对应的点分别为A，B，C，其中b是最小的正整数，a，c
满足|a+2|+（c﹣5）2＝0．
（1）填空：a＝ ，b＝ ，c＝ ；
（2）点A，B，C分别以每秒4个单位长度，1个单位长度，1个单位长度的速度在数轴上同时向右运
动，设运动时间为t秒．
①当AC长为4时，求t的值；







②当点A在点C左侧时（不考虑点A与B，C重合），是否存在一个常数m使得2AC+m•AB的值在
某段运动过程中不随t的改变而改变？若存在，求出m的值；若不存在，请说明理由．











24．（12分）如图（1）：点A、B、C在同一条直线上；AB=AC；AD=AE；DE∥BC；
（1）△ABD与△ACE全等吗？为什么？





（2）将图（1）中△ABD、△ACE分别沿AD、AE折叠；点B的对应点是点F；点C的对应点是点G；
AF、AG分别与DE交于点M、N；连接FG；如图（2）
①△DFM与△EGN全等吗？为什么？





②FG与DE平行吗？为什么？
北师大版七年级（上）数学期末试卷二
参考答案与试题解析

一、选择题
1．【解答】解：因为|﹣3|＝3，|﹣1|＝1，
而3＞1，
所以﹣3＜﹣1＜0＜2，
所以其中最小的一个数是﹣3．
故选：A．
2．【解答】解：760000＝7.6×105．
故选：C．
3．【解答】解：125纳米＝125×10﹣9米＝1.25×10﹣7米．
故选：D．
4．【解答】解：由折线统计图知，气温26℃出现的天数为3天，
∴气温26℃出现的频率是3÷10＝0.3，
故选：D．
5．C
6．B

7．【解答】解：A．此次随机调查的同学数为30÷ ＝100（名），此选项错误；


B．选择“每次分类投放”垃圾的同学有100× ＝55（人），此选项正确；


C．选择“有时分类投放”垃圾所在扇形圆心角的度数为360°× ＝46.8°，此选项正确；

D．选择“从不分类投放”垃圾的同学人数为100﹣（55+30+13）＝2（人），

∴选择“从不分类投放”垃圾的同学占比为 ×100%＝2%，此选项正确；

故选：A．
8．【解答】解：A、两点之间，线段最短，故本选项不合题意；
B、有公共端点是两条射线组成的图形叫做角，故本选项不合题意；
C、若过多边形的一个顶点可以画5条对角线，则这个多边形是八边形，故本选项符合题意；
D、若线段AC＝BC，则点C是线段AB的中点，错误，A、B、C三点不一定共线，故本选项不合题
意；
故选：C．
9．【解答】解：设安排x人生产圆形铁片，则安排（42﹣x）人生产长方形铁片，
依题意得：120x＝2×80（42﹣x）．
故选：C．
10．【解答】解：由题知表2是表1的第三列的一部分，
即a＝15+3＝18，
根据表3在表1中位置规律知b＝m2﹣m，
表4是表一第六列和第七列的一部分，
即c＝35﹣7＝28，
∴a+b+c＝18+m2﹣m+28＝m2﹣m+46，
故选：C．
二、填空题

11．a6
12．8×10-5

13．【解答】解：小张所在公司使用“华为”品牌手机的人数约是600× ＝210

（人），
故答案为：210．
14．【解答】解：根据主视图可得，俯视图中第一列中至少一处有2层；
所以该几何体至少是用6个小立方块搭成的．
故答案为：6．
15．【解答】解：如图．










∵OB⊥AC，∠ABC＝90°，

∴OB＝ ＝ ，
几何体的体积为 ×π×（ ）2×5＝9.6π（cm3）．

故答案为：9.6π．
16．【解答】射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角（大于0°而小于
180°）的平分线有以下两种情况：
①OB平分∠AON时，

∵∠BON＝ ∠AON，


∴6t＝ （180﹣3t），

解得：t＝12；
②OB平分∠AOM时，

∵ ∠AOM＝∠BOM，


∴ t＝180﹣6t，

解得：t＝24．
综上，当t的值分别为12、24秒时，射线OB是由射线OM、射线OA、射线ON中的其中两条组成的
角的平分线．
故答案为：12或24．
5
17．
8
18．y= 36 - 0.3x
三、计算题


19．【解答】解：（1）（ ﹣ ）×（﹣12）﹣|﹣2+5|÷（1﹣ ）

＝﹣ ×（﹣12）﹣3÷

＝2﹣4
＝﹣2；

（2）﹣12020+（﹣2）4×（﹣ ）+（﹣9）÷（﹣1）


＝﹣1+16×（﹣ ）+9
＝﹣1﹣8+9
＝0．
20．【解答】解：

[(x - 3y) - (x - y)(x + y)]÷(- 2y)（2）
解：
2
3
﹣a2•a4+（﹣2a4）2÷a2
（﹣a2）
（1）

=[x2 - 6xy + 9y -(x2 - y )]÷ (- 2y) =[x2 - 6xy + 9y - x2 + y ]÷ (- 2y) =[- 6xy +10 y ]÷ (- 2 y)2 2
2
＝﹣a6﹣a6+4a8÷a2
＝﹣a6﹣a6+4a6
＝2a6；
2 2

=3x - 5yy =-3 时

当 x =2；
原式= 3× 2 - 5×(- 3)
=21
解答题四、


解：（1）小明摸到数字4后；有5个奇数；
分
21．
6、
8；
剩余的8个数字中有3个偶数；
分别是2、

3
= ；
8
p
5
；
8
（小明获胜）
p

（小芳获胜）=5、
7、
9；
所以
别是1、
3、


剩余的8个数字中有4个偶数；分别是2、
分别是1、
4、
6、
8；
（2）小明摸到数字5后；
有4个奇数；

4 14 1
=
8 2
（小明获胜）=
p
（小芳获胜）=
3、
7、
9；
；
；
p
所以

=
8 2
①设B通道每分钟通过的人数是x人，22．
【解答】解：
A通道每分钟通过的人数是2x人，

（2x+x）＝450，
由题意可得：
6×

x＝25，解得：

∴2x＝50，
B通道每分钟通过的人数是25人，答：
A通道每分钟通过的人数是50人；

②设七年级全部学生进校所需时间是y分钟，
（1.2×50+25+50+0.8×25）由题意可得：
×y＝620，

y＝4，解得：

七年级全部学生进校所需时间是4分钟．【解答】解：
（1）
答：
23．

∵|a+2|+（c﹣5）2＝0，
∴a+2＝0，c﹣5＝0，

D
t＝ ．
当1＜t＜ 时，
∴a＝﹣2，c＝5．

∵b是最小的正整数，
∴b＝1．5．
﹣2；
1；

故答案为：
点A表示的数为4t﹣2，点C表示的数为t+5．
（2）
当运动时间为t秒时，
点B表示的数为t+1，

①∵AC＝4，
（t+5）|＝4，∴|4t﹣2﹣

即3t﹣7＝﹣4或3t﹣7＝4，

∴t＝1或t＝ ．

②当4t﹣2＝t+1时，t＝1；


当4t﹣2＝t+5时，

2AC+m•AB＝2[t+5﹣]＝﹣
（4t﹣2）]+m•[t+1﹣
（6+3m）t+14+3m，
当0＜t＜1时，
（4t﹣2）

∵2AC+m•AB的值不随t的变化而变化，
∴6+3m＝0，
∴m＝﹣2；

2AC+m•AB＝2[t+5﹣（t+1）
（3m﹣6）t+14﹣3m，
]+m•[4t﹣2﹣
]＝
（4t﹣2）


∵2AC+m•AB的值不随t的变化而变化，
∴3m﹣6＝0，
∴m＝2．
∴存在一个常数m使得2AC+m•AB的值在某段运动过程中不随t的改变而改变，m的值为﹣2或2．

24．解：

△ABD≌△ACE（1）

∵AD=AE理由：

∴∠ADE=∠AEDC

B
∵DE∥BC
∴∠ADE=∠BAD
∠AED=∠CAE
∴∠BAD=∠CAE
在△ABD和△ACE中A

E
（1）
图

AB = AC
∠BAD
AD



= ∠CAE
= AE
∴△BAD≌△CAE(SAS)


（2）①△DFM≌△EGN
∵△ABD≌△ACE理由：

∴∠BDA=∠CEA ∠B=∠C BD=CE
∠BDA=∠ADF ∠CEA=∠AEG由轴对称可知：

∠B=∠AFD ∠C=∠AGE
BD=DF CE=EG
∴∠ADF=∠AEG ∠AFD=∠AGE DF=EG
又∵∠ADE=∠AEDA


M N

∴∠MDF=∠NEGB
C

E
图
G
（2）

在△MDF和△NEG中
D
∠AFD
DF
F



∠MDF = ∠NEG
= EG
= ∠AGE
∴△MDF≌△NEG(ASA)
②FG∥DE
∵△ABD≌△ACE理由：

∴∠BAD=∠CAE
∴2∠BAD=2∠CAE
即∠BAF=∠CAG
（180°-∠FAG）÷2∴∠BAF=

∵AB=AF=AG=AC
∴∠AFG=（180°-∠FAG）÷2
∴∠BAF=∠AFG
∴FG∥BC
又∵BC∥DE
∴FG∥DE