山东省威海市威海经济技术开发区2022-2023学年八年级下学期期末数学试题（含答案）

这是一份山东省威海市威海经济技术开发区2022-2023学年八年级下学期期末数学试题（含答案），共13页。试卷主要包含了在反比例函数等内容，欢迎下载使用。
2022～2023学年度第二学期质量检测
初三数学
注意事项：
1．本次考试时间120分钟，满分120分．
2．答题时，请务必在题号所指示的区域内作答．作图用2B铅笔．
3．不要求保留精确度的题目，计算结果保留准确值．祝考试成功!
一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得3分，选错、不选或多选，均不得分）
题号
1
2
3
4
5
6
7
8
9
10
答案










1．化简的结果是（）
A．0 B． C． D．
2．下列各式不成立的是（）
A． B．
C． D．
3．已知关于的方程有实数根，则的取值范围为（）
A． B． C．且 D．
4．在反比例函数（为常数）上有三点，若，则的大小关系为（）
A． B． C． D．
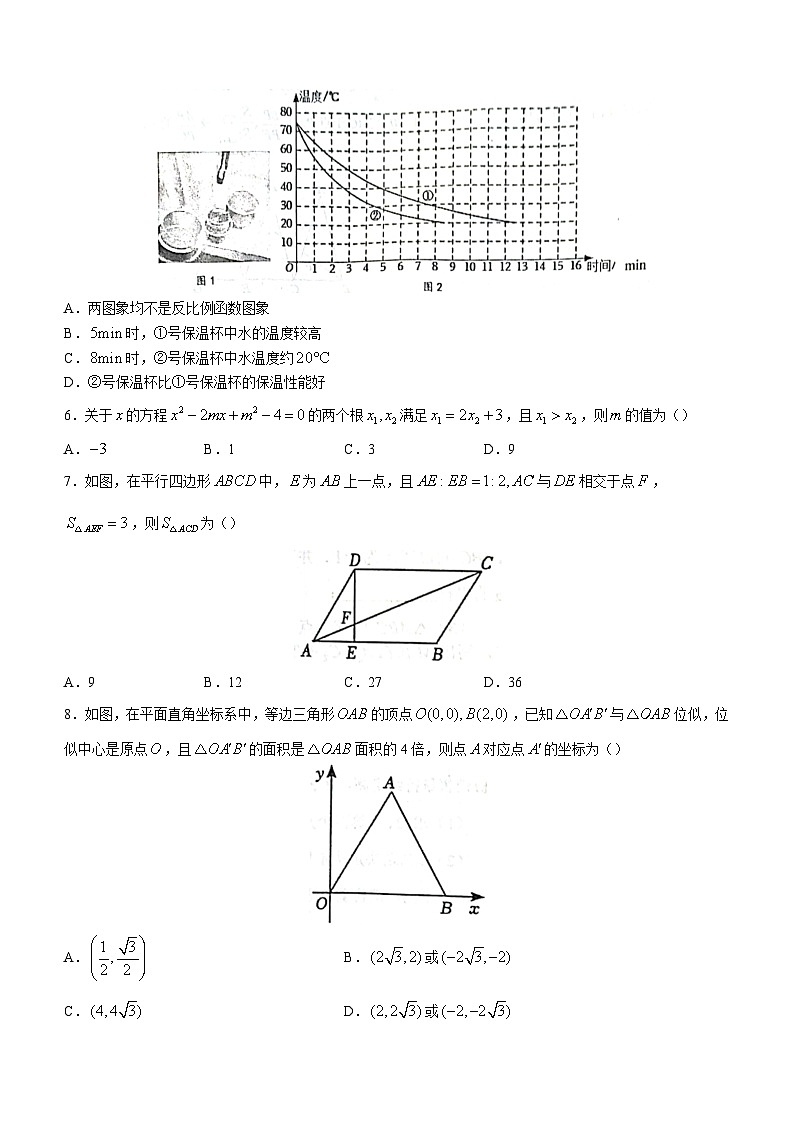
5．小明对“保温杯的保温性能”进行实验，分别取①和②两种带有液晶显示的保温杯用于实验，两保温杯中分别倒入质量和初始温度相同的热水，然后置于冷藏箱中，根据实验数据作出水温随时间变化的图象如图2所示．下面说法错误的是（）

A．两图象均不是反比例函数图象
B．时，①号保温杯中水的温度较高
C．时，②号保温杯中水温度约
D．②号保温杯比①号保温杯的保温性能好
6．关于的方程的两个根满足，且，则的值为（）
A． B．1 C．3 D．9
7．如图，在平行四边形中，为上一点，且与相交于点，，则为（）

A．9 B．12 C．27 D．36
8．如图，在平面直角坐标系中，等边三角形的顶点，已知与位似，位似中心是原点，且的面积是面积的4倍，则点对应点的坐标为（）

A． B．或
C． D．或
9．古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点将一线段分为两线段，使得其中较长的一段是全长与较短的一段的比例中项，把点称为线段的“黄金分割”点．如图，在中，已知，若是边的两个“黄金分割”点，则的面积为（）

A． B． C． D．
10．我国古代数学家研究过一元二次方程的正数解的几何解法．以方程，即为例说明，《方图注》中记载的方法是：构造如图中大正方形的面积是，同时它又等于四个矩形的面积加上中间小正方形的面积，即，因此．小明用此方法解关于的方程时，构造出同样的图形，已知构造出的大正方形的面积为14，小正方形的面积为4，则（）

A． B． C． D．
二、填空题（本大题共6小题，每小题3分，共18分．只要求填出最后结果）
11．代数式有意义的条件是______．
12．若，则______．
13．若非零实数满足，则的值为______．
14．已知，则的化简结果是______．
15．如图，一次函数与反比例函数相交于点，点轴于点轴于点．是线段上的一点，连接，若，则点的坐标为______．

16．如图，在中，为边的中点，连接，将沿折叠得到交于点，连接．则的值为______．

三、解答题（本大题共8小题，共72分）
17．（6分）计算：
（1）；
（2）．
18．（8分）按要求解下列一元二次方程：
（1）（用因式分解法解）；
（2）（用配方法解）；
19．（8分）如图，已知是三个全等的等腰三角形，底边，在同一条直线上，且交于点．求及的值．

20．（8分）如图所示的平面直角坐标系中，的三个顶点坐标分别为，请按如下要求画图：

（1）以坐标原点为旋转中心，将烦时针旋转，得到，请画出；并写出点的对应点的坐标______；
（2）以坐标原点为位似中心，在轴下方，画出的位似图形，使它与的位似比为．并写出点的对应点的坐标______；
（3）内部一点的坐标为，写出在中的对应点的坐标______．
21．（10分）某商场将进价为25元的台灯以40元出售．1月份销售256个，2、3月份销售量持续走高，在售价不变的基础上，3月份的销售量达到400个．
（1）求2、3这两个月销售量的月平均增长率；
（2）该商场决定从4月份进行降价促销，经调查发现，台灯价格在3月份的基础上，每个降价1元，销售量可增加4个，若商场要想使4月份销售这种台灯获利4200元，则台灯售价应定为多少元?
22．（10分）如图所示，一次函数的图象与反比例函数的图象交于．

（1）与反比例函数和一次的数的解析式；
（2）根据图象直接写出不等式的解集；
（3）在轴上存在一点，求使为直角三角形点的坐标．
23．（11分）如图，在平面直角坐标系中，反比例函数的图象经过点，四边形是菱形，点在轴正半轴上，点的坐标是．

（1）求反比例函数的解析式；
（2）点在边上，且，过点作轴，交反比例函数的图象于点，求点的坐标．
24．（11分）如图，在四边形中，，点在边上，且，，作交线段于点，连接．

（1）求证：；
（2）若，求的长．
经区初中数学答案（初三）
一、选择（本大题共10小题，每小题3分，共30分）
1—5BCDCD 6—10CDDAD
二、填空（本大题共6小题，每小题3分，共18分）
11．；12．；13．；14．；15．；16．；
三、解答（72分）
17．（6分）
（1）



．
（2）原式

．
18．（8分）（1），
，
或，
；
（2）配方
；
19．（8分）
解：∵是三个全等的等腰三角形，
∴．
∴．
，．

．
．
20．（8分）
解：（1）如图，即为所求，其中点的对应点的坐标为．

（2）如图所示，即为所求，点的对应点的坐标为
（3）在中的对应点的坐标．
21．（10分）
（1）设2、3这两个月销售量的月平均增长率为，
则：，


（舍），，
答：2、3这两个月销售量的月平均增长率为．
（2）设每个降价元，
则：，
整理得：，
解得：（舍），，
所以售价元
答：售价定为35元在4月份可获利4200元．
22．（10分）
解：（1）如图，即为所求．
点的坐标为
（2）如图，即为所求．
点的坐标为
（3）的坐标为
22．（10分）
解：（1）把代入，∴，
∴反比例函数的解析式是；
把代入得．
把、分别代入中，
得，解得
∴一次函数的解析式为；
（2）或
（3）∵为直角三角形，
∴或，
①当时，即轴，∴，
②当时，设，
∵，
∴，解得，
∴，
综上所述，使为直角三角形的点的坐标为或．
23．（11分）
解：（1）根据题意，过点作轴，垂足为，
∵四边形是菱形，
设点为，∴，
∵点为，∴，
∴，
在直角中，由勾股定理得，
即，解得：，
∴，∴，
∴点的坐标为，
把点代入，得，
∴反比例函数的解析式为；

（2）作轴，垂足分别为，交于点，
∵，∴，
∵，
∴四边形是平行四边形，，
∴，
，
∴，
∵点的坐标为，∴，
∴，∴，
∴，
∴点的纵坐标为16，
∵轴，∴点的纵坐标为16，
∵点在双曲线上，∴，
解得，
∴点的坐标为．

24．（11分）（1）∵，；
，，
，，
，
∴四边形是平行四边形
∴∴
在与中．
，∴

（2）∵，∴，
在中，，∴，∴，
又∵，∴，
在与中
，∴；
∴；
∵，∴；
∵，∴；∴，
∴，∴或（舍）；
∴