北京市2023年中考九年级数学一模填空压轴题分类汇编

这是一份北京市2023年中考九年级数学一模填空压轴题分类汇编，共14页。
填空压轴题汇编
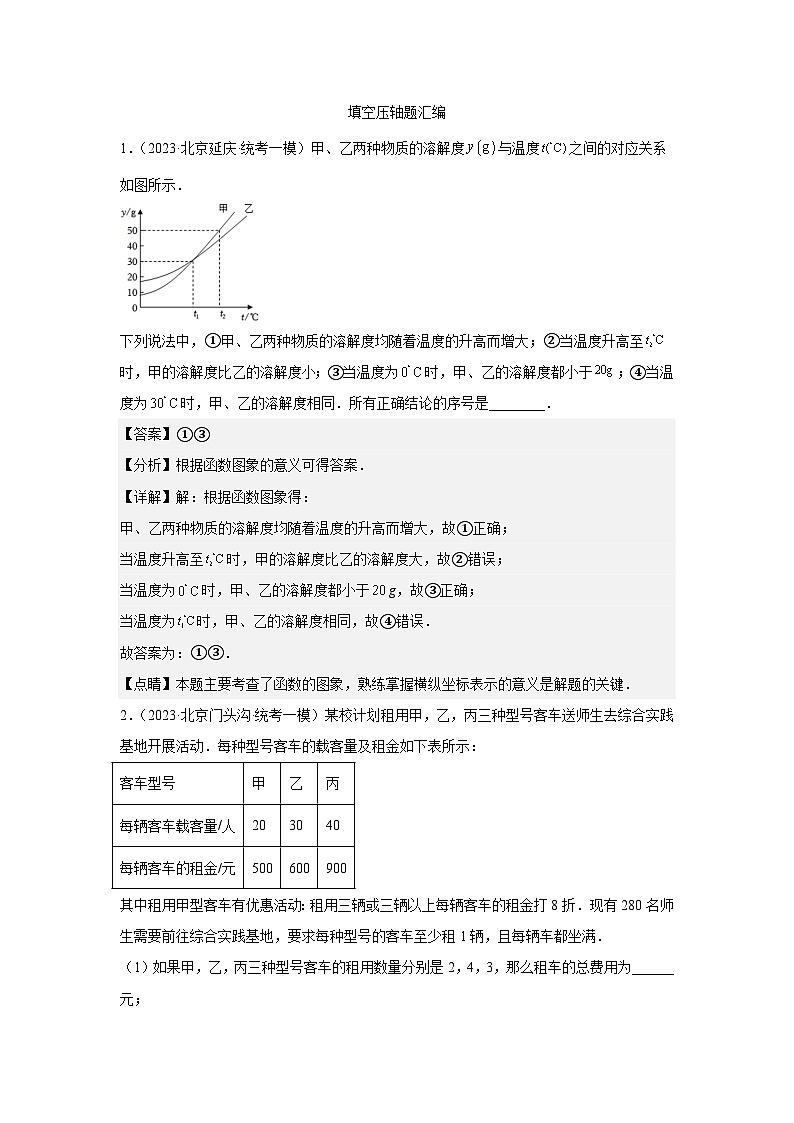
1．（2023·北京延庆·统考一模）甲、乙两种物质的溶解度与温度之间的对应关系如图所示．

下列说法中，①甲、乙两种物质的溶解度均随着温度的升高而增大；②当温度升高至时，甲的溶解度比乙的溶解度小；③当温度为时，甲、乙的溶解度都小于；④当温度为时，甲、乙的溶解度相同．所有正确结论的序号是________．
【答案】①③
【分析】根据函数图象的意义可得答案．
【详解】解：根据函数图象得：
甲、乙两种物质的溶解度均随着温度的升高而增大，故①正确；
当温度升高至时，甲的溶解度比乙的溶解度大，故②错误；
当温度为时，甲、乙的溶解度都小于g，故③正确；
当温度为时，甲、乙的溶解度相同，故④错误．
故答案为：①③．
【点睛】本题主要考查了函数的图象，熟练掌握横纵坐标表示的意义是解题的关键．
2．（2023·北京门头沟·统考一模）某校计划租用甲，乙，丙三种型号客车送师生去综合实践基地开展活动．每种型号客车的载客量及租金如下表所示：
客车型号
甲
乙
丙
每辆客车载客量/人
20
30
40
每辆客车的租金/元
500
600
900
其中租用甲型客车有优惠活动：租用三辆或三辆以上每辆客车的租金打8折．现有280名师生需要前往综合实践基地，要求每种型号的客车至少租1辆，且每辆车都坐满．
（1）如果甲，乙，丙三种型号客车的租用数量分别是2，4，3，那么租车的总费用为______元；
（2）如果租车的总费用最低，那么甲，乙，丙三种型号客车的租用数量可以分别是______．
【答案】 6100 9，2，1或6，4，1
【分析】（1）列式计算即可求解；
（2）设甲，乙，丙三种型号客车的租用数量分别是a，b，c，分①，或②，或③，三种情况讨论，利用a，b，c都是正整数以及一次函数的性质求解即可．
【详解】解：（1）依题意得(元)；
故答案为：6100；
（2）设甲，乙，丙三种型号客车的租用数量分别是a，b，c，租车的总费用为y，
则，即，
整理得，
∵a，b，c都是正整数，∴则必须是3的倍数，
∴①，或②，或③，；
分类讨论，
①当，，时，，不合题意，舍去；
当时，，，
∴，
∵，
∴c最小时，y最小，即时，最小值为5700元，此时；
②当，，时，由（1）得，不合题意，舍去；
当时，，，
∴，
∵，
∴c最小时，y最小，即时，最小值为5700元，此时；
③当，，时，，不合题意，舍去；
综上，如果租车的总费用最低，那么甲，乙，丙三种型号客车的租用数量可以分别是9，2，1或6，4，1．
故答案为：9，2，1或6，4，1．
【点睛】本题考查了一次函数的应用，正确的分类是解题的关键，注意租用甲型客车有优惠活动．
3．（2023·北京通州·统考一模）某学校带领150名学生到农场参加植树劳动，学校同时租用A，B，C三种型号客车去农场，其中A，B，C三种型号客车载客量分别为40人、30人、10人，租金分别为700元、500元、200元．为了节省资金，学校要求每辆车必须满载，并将学生一次性送到农场植树，请你写出一种满足要求的租车方案__________，满足要求的几种租车方案中，最低租车费用是__________元．
【答案】 租用A型号客车1辆，B型号客车3辆，C型号客车2辆（答案不唯一） 2600
【分析】设租用A，B，C三种型号客车分别为辆，根据题意列出方程进行求解即可．
【详解】解：设租用A，B，C三种型号客车分别为辆，由题意，得：
，
∵均为正整数，
∴或或或或，
∴可以租用A型号客车1辆，B型号客车3辆，C型号客车2辆（答案不唯一）；
当租用A型号客车1辆，B型号客车1辆，C型号客车8辆时，花费的费用为：元；
当租用A型号客车1辆，B型号客车2辆，C型号客车5辆时，花费的费用为：元；
当租用A型号客车1辆，B型号客车3辆，C型号客车2辆时，花费的费用为：元；
当租用A型号客车2辆，B型号客车1辆，C型号客车4辆时，花费的费用为：元；
当租用A型号客车2辆，B型号客车2辆，C型号客车1辆时，花费的费用为：元；
故最低租车费用为：元；
故答案为：租用A型号客车1辆，B型号客车3辆，C型号客车2辆（答案不唯一）；2600．
【点睛】本题考查三元一次方程的实际应用．找准等量关系，正确的列出方程，是解题的关键．
4．（2023·北京丰台·统考一模）临近端午，某超市准备购进小枣粽、豆沙粽、肉粽共200袋（每袋均为同一品种的粽子），其中小枣粽每袋6个，豆沙粽每袋4个，肉粽每袋2个，为了促销，超市计划将所购粽子组合包装，全部制成A，B两种套装销售，套装为每袋小枣粽4个，豆沙粽2个；B套装为每袋小枣粽2个，肉粽2个．
（1）设购进的小枣粽x袋，豆沙粽y袋，则购进的肉粽的个数为________（用含x，y的代数式表示）；
（2）若肉粽的进货袋数不少于三种粽子进货总袋数的，则豆沙粽最多购进_______袋．
【答案】 40
【分析】（1）根据题意可得购进的肉粽袋，即可求解；
（2）根据题意可得购进的小枣粽的个数为个，豆沙粽的个数为个，从而得到套装为套，套装为套，再由套装每袋小枣粽4个，B套装每袋小枣粽2个，可得，从而得到，然后根据肉粽的进货袋数不少于三种粽子进货总袋数的，可得，即可．
【详解】解：（1）设购进的小枣粽x袋，豆沙粽y袋，则购进的肉粽袋，
∴购进的肉粽的个数为个；
故答案为：
（2）根据题意得：购进的小枣粽的个数为个，豆沙粽的个数为个，
∵套装豆沙粽2个；B套装肉粽2个．
∴套装为套，套装为套，
∵套装每袋小枣粽4个，B套装每袋小枣粽2个，
∴，
解得：，
∵肉粽的进货袋数不少于三种粽子进货总袋数的，
∴，
即，
解得：，
∴豆沙粽最多购进40袋；
故答案为：40
【点睛】本题主要考查了二元一次方程的应用，一元一次不等式的应用，解答本题的关键是正确的表示各种粽子的袋数，个数，根据肉粽的进货数量的要求列出不等式求解验证．
5．（2023·北京房山·统考一模）为进一步深化“创城创卫”工作，传播健康环保的生活理念，房山区持续推进垃圾分类工作．各乡镇（街道）的党员、志愿者纷纷参与“桶前值守”，在垃圾桶旁监督指导居民对垃圾进行分类．某垃圾值守点有甲、乙、丙、丁四名志愿者，某一天每人可参与值守时间段如下表所示：
志愿者
可参与值守时间段1
可参与值守时间段2
甲
6：00-8：00
16：00-18：00
乙
6：30-7：30
17：00-20：00
丙
8：00-11：00
18：00-19：00
丁
7：00-10：00
17：30-18：30
已知每名志愿者一天至少要参加一个时间段的值守，任意时刻垃圾值守点同时最多需要2名志愿者值守，则该值守点这一天所有参与值守的志愿者的累计值守时间最短为__________小时，最长为__________小时（假设志愿者只要参与值守，就一定把相应时间段全部值完）．
【答案】 13 14
【分析】先列表表示上午值守时间安排，下午值守时间安排，再结合每名志愿者一天至少要参加一个时间段的值守，任意时刻垃圾值守点同时最多需要2名志愿者值守，分析得出答案即可．
【详解】解：上午值守时间如下表，








甲
甲
甲
甲
甲



乙

乙
乙




丙




丙
丙
丙
丁


丁
丁
丁
丁

下午值守时间安排如下表：







甲
甲
甲
甲



乙

乙
乙
乙
乙
乙
丙



丙
丙

丁


丁
丁


∵任意时刻垃圾值守点同时最多需要2名志愿者值守，
∴下午的值守同时安排甲，乙，丙值守，则丁不能参与，
所以下午值守的最短时长为甲，乙值守时，共（小时），
∵每名志愿者一天至少要参加一个时间段的值守，
∴上午丙，丁必安排值守，而甲必值守，
∴总时长为：（小时），
∴该值守点这一天所有参与值守的志愿者的累计值守时间最短为（小时）；
∴当下午同时安排甲，乙，丙值守，最长总时长为（小时），
上午可先安排甲，丙，丁值守，总时长为（小时），
∴上午值守时间最长为小时，
∴该值守点这一天所有参与值守的志愿者的累计值守时间最长为（小时）；
故答案为：13；14
【点睛】本题考查的是逻辑推理，理解题意，找到突破口，逐步分析是解本题的关键．
6．（2023·北京平谷·统考一模）某货运公司临时接到一个任务，从工厂同时运送A、B两种货物各20箱到展馆，货运公司调派甲货车运送A种货物，乙货车运送B种货物，A种货物每箱80千克，B种货物每箱70千克，因为两种货物包装箱完全一样，装运工人一时疏忽两车虽然所装货物数量正确，但部分货物却装混了．运送途中安检时，两车过地秤，发现甲车比乙车的货物重160千克，则甲、乙两车各有______箱货物装错，到达展馆，为了尽快把货物区分开，乙车司机借来了一台最多可以称300千克的秤精选最优称重方案，根据被错装货物出现的所有可能情况，最多需要称______次就能把乙车上装错的货物区分出来．
【答案】 2 8
【分析】设甲、乙两车各有x箱货物装错，根据甲车比乙车的货物重160千克，可得，可得，将乙车上的货物平均分为5堆，每堆4箱，将5堆货物最多称4次，其中重量为280千克的堆里没有装错，可以判断出错误的堆数；装错的货物可以在1堆里，也可以在2堆里；如果装错的货物可以在1堆里，再最多称4次可以将装错的2箱货物区分出来；如果装错的货物可以在2堆里，再最多称3次可以将装错的2箱货物区分出来，所以最多需要称8次就能把乙车上装错的货物区分出来．
【详解】解：设甲、乙两车各有x箱货物装错，根据题意得：

解得：，
将乙车上的货物平均分为5堆，每堆4箱，将5堆货物最多称4次，其中重量为280千克的堆里没有装错，可以判断出错误的堆数；装错的货物可以在1堆里，也可以在2堆里；如果装错的货物可以在1堆里，先称两箱，如果这个两箱质量和为140或160千克，则可判断哪两箱是装错的，若这个两箱质量和为150千克，再选择这两箱中其中一箱称重量，就可以哪一箱是装错的，另两箱也同操作即可，最多称3次可以将装错的2箱货物区分出来；如果装错的货物可以在2堆里，每一堆都先称两箱，判断装错的在哪两箱中，然后在这两箱中称其中一箱就可以判断了，最多称4次可以将装错的2箱货物区分出来，所以最多需要称8次就能把乙车上装错的货物区分出来，
故答案为：2，8．
【点睛】本题考查了一元一次方程的应用和推理，解题的关键是正确推理．
7．（2023·北京西城·统考一模）A，B，C三种原料每袋的重量（单位：kg）依次是1，2，3，每袋的价格（单位：万元）依次是3，2，5．现生产某种产品需要A，B，C这三种原料的袋数依次为（均为正整数），则生产这种产品时需要的这三类原料的总重量W（单位：kg）=__________（用含的代数式表示）：为了提升产品的品质，要求，当的值依次是_______时，这种产品的成本最低．
【答案】 1，5，1
【分析】根据重量等于单袋重量乘以袋数，列式计算即可；运用不等式的基本性质计算即可．
【详解】∵A，B，C三种原料每袋的重量（单位：kg）依次是1，2，3，需要A，B，C这三种原料的袋数依次为（均为正整数），
∴，
故答案为：；
设总成本价为M元，根据题意，得，
∵均为正整数，，
∴，
当且仅当，时，成本最低，此时，
故，
故答案为：1,5,1．
【点睛】本题考查了不等式的应用，熟练掌握不等式的性质是解题的关键．
8．（2023·北京海淀·统考一模）某陶艺工坊有A和B两款电热窑，可以烧制不同尺寸的陶艺品．两款电热窑每次可同时放置陶艺品的尺寸和数量如下表所示．

大
中
小
A
8
15
25
B
0
10
20
烧制一个大尺寸陶艺品的位置可替换为烧制两个中尺寸或六个小尺寸陶艺品，但烧制较小陶艺品的位置不能替换为烧制较大陶艺品．
某批次需要生产10个大尺寸陶艺品，50个中尺寸陶艺品，76个小尺寸陶艺品．
（1）烧制这批陶艺品，A款电热窑至少使用_________次；
（2）若A款电热窑每次烧制成本为55元，B款电热窑每次烧制成本为25元，则烧制这批陶艺品成本最低为_________元．
【答案】 2
【分析】（1）根据需要生产10个大尺寸陶艺品，A款电热窑每次烧制8个大尺寸陶艺品，B款电热窑每次烧制0个大尺寸陶艺品即可得到答案；
（2）要使成本最低，则在保证能够完成烧制任务的前提下，A款电热窑的使用次数要保证使用次数最少，且B款电热窑的使用次数也要最少，据此求解即可．
【详解】解：（1）∵需要生产10个大尺寸陶艺品，A款电热窑每次最多可放8个大尺寸陶艺品，B款电热窑不能放大尺寸陶艺品，且烧制较小陶艺品的位置不能替换为烧制较大陶艺品，
∴烧制这批陶艺品，A款电热窑至少使用2次，
故答案为：2；
（2）∵A款电热窑每次烧制成本为55元，B款电热窑每次烧制成本为25元，
∴要使成本最低，则在保证能够完成烧制任务的前提下，A款电热窑的使用次数要保证使用次数最少，且B款电热窑的使用次数也要最少；
当A款电热窑的使用次数为2次时，则可以烧制10个大尺寸陶艺品，个中尺寸陶艺品，个小尺寸陶艺品，
∴在此种情形下，只需要B款电热窑的使用次数1次即可完成任务，
∴烧制这批陶艺品成本最低为，
故答案为：．
【点睛】本题主要考查了一元一次不等式的实际应用，正确理解题意是解题的关键．
9．（2023·北京顺义·统考一模）某京郊民宿有二人间、三人间、四人间三种客房供游客住宿，某旅游团有25位女士游客准备同时住这三种客房共8间，如果每间客房都要住满，请写出一种住宿方案__________；如果二人间、三人间、四人间三种客房的收费标准分别为300元/间、360元/间、400元/间，则最优惠的住宿方案是_________．
【答案】 二人间2间，三人间3间，四人间3间（答案不唯一）； 二人间3间，三人间1间，四人间4间．
【分析】设二人间、三人间分别需要间，间，则四人间需要间，则，整理得：，再利用方程的非负整数解可得答案；设住宿总费用为：元，而，则，再利用一次函数的性质解答即可．
【详解】解：设二人间、三人间分别需要间，间，则四人间需要间，则
，
整理得：，
∵，，都为非负整数，
∴当时，，，
∴可行的住宿方案为：二人间2间，三人间3间，四人间3间；
设住宿总费用为：元，而，则



，
∵，
∴当最大，有最小值，
∵，，，都为非负整数，
∴时最大，
此时，；
∴最佳住宿方案为：二人间3间，三人间1间，四人间4间．
故答案为：二人间2间，三人间3间，四人间3间（答案不唯一）；二人间3间，三人间1间，四人间4间．
【点睛】本题考查的是二元一次方程的整数解的应用，一次函数的应用，理解题意，构建方程与一次函数是解本题的关键．
10．（2023·北京·统考一模）某工厂用甲、乙两种原料制作，，三种型号的工艺品，三种型号工艺品的重量及所含甲、乙两种原料的重量如下：
工艺品型号
含甲种原料的重量
含乙种原料的重量
工艺品的重量
A
3
4
7
B
3
2
5
C
2
6
5
现要用甲、乙两种原料共，制作5个工艺品，且每种型号至少制作1个．
（1）若原料恰好全部用完，则制作型工艺品的个数为__________个；
（2）若使用甲种原料不超过，同时使用乙种原料最多，则制作方案中，，三种型号的工艺品的个数依次为__________．
【答案】 3 2，1，2
【分析】（1）设制作A、B、C三种类型的工艺品分别为x个，y个，z个，根据题意列出方程组求解即可；
（2）设制作A、B、C三种类型的工艺品分别为a个，b个，c个，根据题意推出，再由使用乙种原料最多，则A、C的个数要尽可能的多，B的个数要尽可能的少，即可得到．
【详解】解：（1）设制作A、B、C三种类型的工艺品分别为x个，y个，z个，
由题意得，，
解得，
∴制作型工艺品的个数为3个，
故答案为：3；
（2）设制作A、B、C三种类型的工艺品分别为a个，b个，c个，
由题意得，，
∴，
∴，
∵使用乙种原料最多，
∴A、C的个数要尽可能的多，B的个数要尽可能的少，
∴，
故答案为：2，1，2．
【点睛】本题主要考查了三元一次方程组的实际应用，不等式和方程相结合的问题，正确理解题意列出对应的方程和不等式是解题的关键．
11．（2023·北京朝阳·统考一模）一个33人的旅游团到一家酒店住宿，酒店的客房只剩下4间一人间和若干间三人间，住宿价格是一人间每晚100元，三人间每晚130元（说明：男士只能与男士同住，女士只能与女士同住，三人间客房可以不住满，但每间每晚仍需支付130元）．
（1）若该旅游团一晚的住宿房费为1530元，则他们租住了_______间一人间；
（2）若该旅游团租住了3间一人间，且共有19名男士，则租住一晚的住宿房费最少为______元．
【答案】 1 1600
【分析】（1）设它们租住了x间1人间，y间三人间，且x、y均为自然数，根据题意列出不等式组，解不等式组即可求解；
（2）33人中共有19名男士，则女士有14名，根据，，再结合该团已经租住了3间1人间，可得：安排2名女士和1名男士住1人间，剩下的18名男士和12名女士住三人间，即可最节省，问题得解．
【详解】（1）设它们租住了x间1人间，y间三人间，且x、y均为自然数，
根据题意有：，
解得：，
∵且x、y均为自然数，
∴可以取0和1，
当时，，不为自然数，舍去，
当时，，
即他们租住了1间一人间；
（2）33人中共有19名男士，则女士有14名，
∵，，
又∵该团已经租住了3间1人间，
∴安排2名女士和1名男士住1人间，剩下的18名男士和12名女士住三人间，即可最节省，
即：（元），
故答案为：1，1600．
【点睛】本题考查了不等式组的应用以及有理数的运算的应用，明确题意列出不等式组，是解答本题的关键．