第12章全等三角形综合训练试题（Word版附解析）

这是一份第12章全等三角形综合训练试题（Word版附解析），共5页。
第十二章综合训练一、选择题1.下列说法正确的是(　　)A.有三个角对应相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.有两个角与其中一个角的对边对应相等的两个三角形全等D.有两个角对应相等,还有一条边也相等的两个三角形全等2.如图,△ABC≌△AEF,AC与AF是对应边,则∠EAC等于(　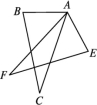　)A.∠ACBB.∠CAFC.∠BAFD.∠BAC3.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有(　　)　　　　　　　　　　　　　　　　A.1组 B.2组 C.3组 D.4组4.如图,将两根钢条AA',BB'的中点O连在一起,使AA',BB'能绕着点O自由转动,就做成了一个测量工具,则A'B'的长等于内槽宽AB,其中判定△OAB≌△OA'B'的理由是(　　)A.SAS B.ASA C.SSS D.HL5.如图,AC=BD,AB=CD,图中全等的三角形共有 (　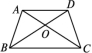　)A.2对 B.3对 C.4对 D.5对6.如图,AB∥CF,DE=EF,AB=10,CF=6,则DB等于 (　　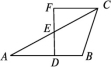)A.3 B.4 C.5 D.67.要测量河两岸相对的两点A,B间的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上,如图,可以证明△EDC≌△ABC,得到DE=AB,因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是(　　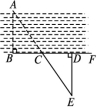)A.SAS B.ASA C.SSS D.HL8.如图,在△ABC中,已知AD⊥BC,CE⊥AB,垂足分别为点D,E,AD,CE交于点H.若EH=EB=3,AE=4,则CH的长是(　　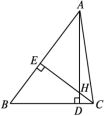)A.1 B.2 C.3 D.4二、填空题9.如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1的度数是　　　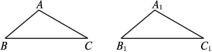　　. 10.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当的条件:　　　　　　　　　　　　　　　　,使△AEH≌△CEB. 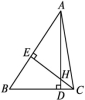11.雨伞开闭过程中某时刻的截面图如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC.当O沿AD滑动时,雨伞开闭.雨伞开闭过程中,∠BAD与∠CAD　　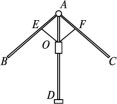　　　　. 12.如图,在直角三角形ABC中,∠C=90°,AC=10 cm,BC=5 cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP=　　　　　cm时,才能使△ABC和△QPA全等. 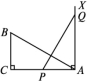三、解答题13.如图,C为线段AB上一点,AD∥EB,AC=BE,AD=BC.求证:△ACD≌△BEC. 14.如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.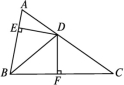        15.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.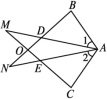求证:(1)BD=CE;(2)∠M=∠N.         16.如图,已知Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.(1)图中还有几对全等三角形,请你一一列举;(2)求证:CF=EF.
第十二章综合训练一、选择题1.C　2.C　3.C　4.A5.B　根据全等三角形的判定可得图中全等的三角形有:△ADB和△DAC;△ABC和△DCB;△ABO和△DCO.6.B7.B8.A二、填空题9.30°10.AH=CB(或EH=EB或AE=CE)　根据“AAS”需要添加AH=CB或EH=EB;根据“ASA”需要添加AE=CE.11.相等　∵AE=AB,AF=AC,AB=AC,∴AE=AF.又∵OE=OF,OA=OA,∴△AOE≌△AOF(SSS).∴∠BAD=∠CAD.12.5或10三、解答题13.证明∵AD∥BE,∴∠A=∠B.在△ACD和△BEC中,∵∴△ACD≌△BEC.14.解∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,∴DE=DF.∵S△ABC=28,AB=6,BC=8,∴×6×DE+×8×DF=28,∴DE=DF=4.15.证明(1)在△ABD和△ACE中,∴△ABD≌△ACE(SAS).∴BD=CE.(2)∵∠1=∠2,∴∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM.由(1),得△ABD≌△ACE,∴∠B=∠C.在△ACM和△ABN中,∴△ACM≌△ABN(ASA),∴∠M=∠N.16.(1)解2对,分别为△ADC≌△ABE,△CDF≌△EBF.(2)证法一∵Rt△ABC≌Rt△ADE,∴AC=AE,AD=AB,∠CAB=∠EAD,∴∠CAB-∠DAB=∠EAD-∠DAB,即∠CAD=∠EAB.∴△ACD≌△AEB(SAS).∴CD=EB,∠ADC=∠ABE.又∠ADE=∠ABC,∴∠CDF=∠EBF.又∠DFC=∠BFE,∴△CDF≌△EBF(AAS).∴CF=EF.证法二如图,连接AF.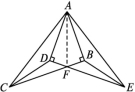∵Rt△ABC≌Rt△ADE,∴AB=AD,BC=DE.又AF=AF,∠ABC=∠ADE=90°,∴Rt△ABF≌Rt△ADF(HL).∴BF=DF.又BC=DE,∴BC-BF=DE-DF.∴CF=EF.