高考数学一轮复习教案 第3章_第1节_任意角、弧度制及任意角的三角函数（含答案解析）

这是一份高考数学一轮复习教案 第3章_第1节_任意角、弧度制及任意角的三角函数（含答案解析），共10页。


1．角的概念的推广
(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．
(2)分类eq \b\lc\{\rc\ (\a\vs4\al\c1(按旋转方向不同分为正角、负角、零角.,按终边位置不同分为象限角和轴线角.))
(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋k·360°，k∈Z}．
2．弧度制的定义和公式
(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度．正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0.
(2)公式
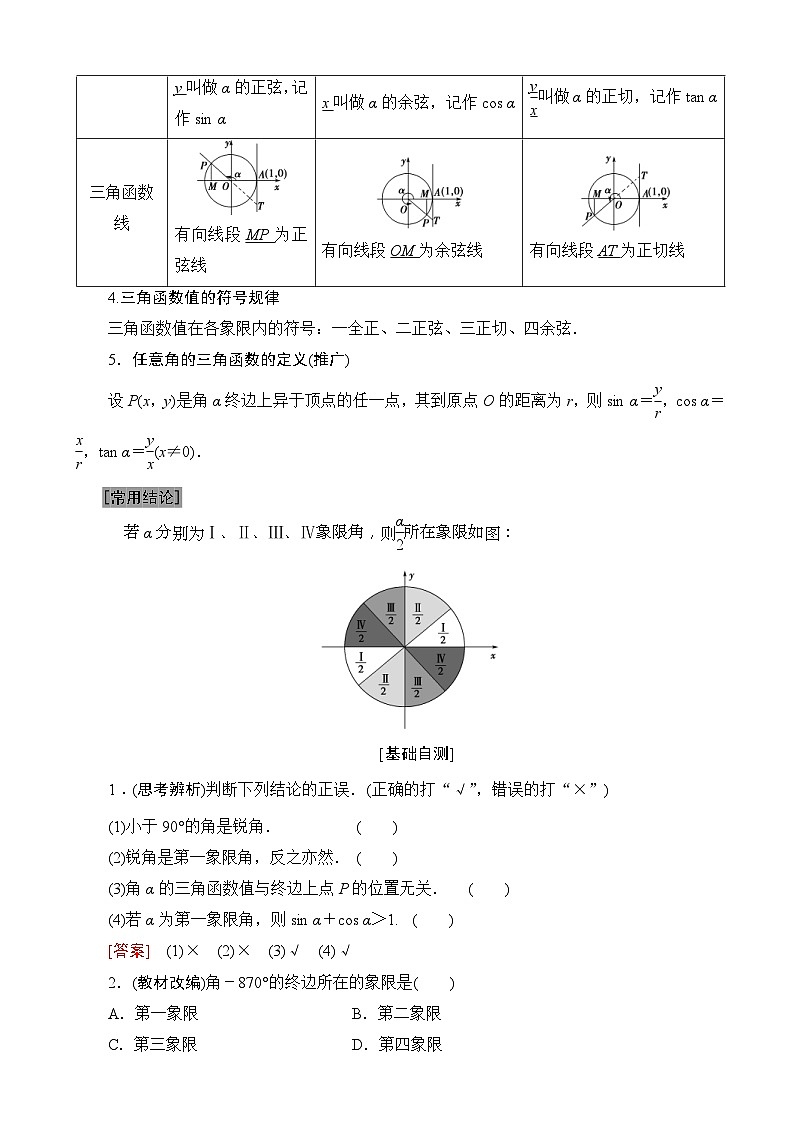
3.任意角的三角函数
4.三角函数值的符号规律
三角函数值在各象限内的符号：一全正、二正弦、三正切、四余弦．
5．任意角的三角函数的定义(推广)
设P(x，y)是角α终边上异于顶点的任一点，其到原点O的距离为r，则sin α＝eq \f(y,r)，cs α＝eq \f(x,r)，tan α＝eq \f(y,x)(x≠0)．
eq \([常用结论])
若α分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ象限角，则eq \f(α,2)所在象限如图：
[基础自测]
1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)
(1)小于90°的角是锐角．( )
(2)锐角是第一象限角，反之亦然．( )
(3)角α的三角函数值与终边上点P的位置无关．( )
(4)若α为第一象限角，则sin α＋cs α＞1.( )
[答案] (1)× (2)× (3)√ (4)√
2．(教材改编)角－870°的终边所在的象限是( )
A．第一象限 B．第二象限
C．第三象限 D．第四象限
C [－870°＝－2×360°－150°，－870°和－150°的终边相同，故－870°的终边在第三象限．]
3．若角θ同时满足sin θ＜0且tan θ＜0，则角θ的终边一定位于( )
A．第一象限 B．第二象限
C．第三象限 D．第四象限
D [由sin θ＜0知角θ的终边在三、四象限或y轴负半轴上，由tan θ＜0知角θ的终边在二、四象限，故角θ的终边在第四象限，故选D.]
4．(教材改编)已知角α的终边与单位圆的交点为Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，y))，则sin α＝( )
A.eq \f(\r(,3),2) B．±eq \f(\r(,3),2) C.eq \f(\r(,2),2) D．±eq \f(\r(,2),2)
B [由题意知|r|2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))2＋y2＝1，所以y＝±eq \f(\r(,3),2).由三角函数定义知sin α＝y＝±eq \f(\r(,3),2).]
5．在单位圆中，200°的圆心角所对的弧长为( )
A．10π B．9π C.eq \f(9,10)π D.eq \f(10,9)π
D [单位圆的半径r＝1,200°的弧度数是200×eq \f(π,180)＝eq \f(10,9)π，由弧长公式得l＝eq \f(10,9)π.]
1．若α＝k·180°＋45°(k∈Z)，则α在( )
A．第一或第三象限 B．第一或第二象限
C．第二或第四象限 D．第三或第四象限
A [当k＝2n(n∈Z)时，α＝2n·180°＋45°＝n·360°＋45°，α为第一象限角；
当k＝2n＋1(n∈Z)时，α＝(2n＋1)·180°＋45°＝n·360°＋225°，α为第三象限角，所以α为第一或第三象限角．故选A.]
2．若角α是第二象限角，则eq \f(α,2)是( )
A．第一象限角 B．第二象限角
C．第一或第三象限角 D．第二或第四象限角
C [∵α是第二象限角，∴eq \f(π,2)＋2kπ＜α＜π＋2kπ，k∈Z，
∴eq \f(π,4)＋kπ＜eq \f(α,2)＜eq \f(π,2)＋kπ，k∈Z.
当k为偶数时，eq \f(α,2)是第一象限角；
当k为奇数时，eq \f(α,2)是第三象限角．
综上，eq \f(α,2)是第一或第三象限角，故选C.]
3．与－2 015°终边相同的最小正角是________．
145° [－2 015°＝6×(－360°)＋145°，因此与－2 015°终边相同的最小正角是145°.]
4．终边在直线y＝eq \r(3)x上的角的集合是________．
{β|β＝60°＋k·180°，k∈Z} [如图，直线y＝eq \r(3)x过原点，倾斜角为60°，
在0°～360°范围内，
终边落在射线OA上的角是60°，终边落在射线OB上的角是240°，所以以射线OA，OB为终边的角的集合为：
S1＝{β|β＝60°＋k·360°，k∈Z}，
S2＝{β|β＝240°＋k·360°，k∈Z}，
所以角β的集合S＝S1∪S2
＝{β|β＝60°＋k·360°，k∈Z}∪{β|β＝60°＋180°＋k·360°，k∈Z}
＝{β|β＝60°＋2k·180°，k∈Z}∪{β|β＝60°＋(2k＋1)·180°，k∈Z}
＝{β|β＝60°＋k·180°，k∈Z}．]
[规律方法] 1.象限角的两种判断方法
(1)图象法：在平面直角坐标系中，作出已知角并根据象限角的定义直接判断已知角是第几象限角．
(2)转化法：先将已知角化为k·360°＋α(0°≤α＜360°，k∈Z)的形式，即找出与已知角终边相同的角α，再由角α终边所在的象限判断已知角是第几象限角．
2．终边在某直线上角的求法四步骤
(1)数形结合，在平面直角坐标系中画出该直线．
(2)按逆时针方向写出[0,2π)内的角．
(3)再由终边相同角的表示方法写出满足条件角的集合．
(4)求并集化简集合．
【例1】 (1)已知扇形周长为10，面积是4，求扇形的圆心角；
(2)已知扇形周长为40，当它的半径和圆心角分别取何值时，扇形的面积最大？
[解] (1)设圆心角是θ，半径是r，则
eq \b\lc\{\rc\ (\a\vs4\al\c1(2r＋rθ＝10，,\f(1,2)θ·r2＝4，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(r＝1，,θ＝8))(舍去)或eq \b\lc\{\rc\ (\a\vs4\al\c1(r＝4，,θ＝\f(1,2)，))
∴扇形的圆心角为eq \f(1,2).
(2)设圆心角是θ，半径是r，则2r＋rθ＝40.
又S＝eq \f(1,2)θr2＝eq \f(1,2)r(40－2r)＝r(20－r)＝－(r－10)2＋100≤100.
当且仅当r＝10时，Smax＝100，此时2×10＋10θ＝40，θ＝2，∴当r＝10，θ＝2时，扇形的面积最大．
[规律方法] 解决有关扇形的弧长和面积问题的常用方法及注意事项
1解决有关扇形的弧长和面积问题时，要注意角的单位，一般将角度化为弧度.
2求解扇形面积的最值问题时，常转化为二次函数的最值问题，利用配方法使问题得到解决.
3在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形.
(1)若扇形的圆心角α＝120°，弦长AB＝12 cm，则弧长l＝________cm.
eq \f(8\r(,3),3)π [设扇形的半径为r cm，如图．
由sin 60°＝eq \f(6,r)，得r＝4eq \r(,3) cm，
∴l＝|α|·r＝eq \f(2π,3)×4eq \r(,3)＝eq \f(8\r(,3),3)π cm.]
(2)已知扇形AOB的周长为C，当圆心角为多少时，扇形的面积最大？
[解] 设扇形AOB的半径为r，弧长为l，圆心角为α，由题意可知
eq \b\lc\{\rc\ (\a\vs4\al\c1(C＝l＋2r ①,S＝\f(1,2)lr ②))∴l＝C－2r，代入②可得：S＝eq \f(1,2)(C－2r)·r＝eq \f(C,2)r－r2eq \b\lc\(\rc\)(\a\vs4\al\c1(0＜r＜\f(C,2)))，
∵S＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(r－\f(C,4)))2＋eq \f(C2,16)，0＜r＜eq \f(C,2)，∴当r＝eq \f(C,4)时，S最大，此时l＝C－eq \f(C,2)＝eq \f(C,2)，∴α＝eq \f(l,r)＝2.
►考法1 利用三角函数的定义求值
【例2】 (1)已知点P在角eq \f(4π,3)的终边上，且|OP|＝4，则点P的坐标为( )
A．(－2，－2eq \r(3)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，－\f(\r(3),2)))
C．(－2eq \r(3)，－2) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，－\f(1,2)))
(2)已知角α的终边经过点P(－x，－6)，且cs α＝－eq \f(5,13)，则eq \f(1,sin α)＋eq \f(1,tan α)＝________.
(1)A (2)－eq \f(2,3) [(1)设P(x，y)，由三角函数的定义知，eq \f(y,4)＝sin eq \f(4π,3)，eq \f(x,4)＝cseq \f(4π,3)，即y＝4sineq \f(4π,3)＝－2eq \r(3)，x＝4cseq \f(4π,3)＝－2，即点P的坐标为(－2，－2eq \r(3))，故选A.
(2)r＝eq \r(x2＋36)，由cs α＝－eq \f(5,13)得eq \f(－x,\r(x2＋36))＝－eq \f(5,13)
解得x＝eq \f(5,2)或x＝－eq \f(5,2)(舍去)
所以Peq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(5,2)，－6))，
所以sin α＝－eq \f(12,13)，所以tan α＝eq \f(sin α,cs α)＝eq \f(12,5)，
则eq \f(1,sin α)＋eq \f(1,tan α)＝－eq \f(13,12)＋eq \f(5,12)＝－eq \f(2,3).]
►考法2 三角函数值的符号判定
【例3】 (1)若sin αtan α＜0，且eq \f(cs α,tan α)＜0，则角α是( )
A．第一象限角 B．第二象限角
C．第三象限角 D．第四象限角
(2)sin 2·cs 3·tan 4的值( )
A．小于0 B．大于0
C．等于0 D．不确定
(1)C (2)A [(1)由sin αtan α＜0可知sin α，tan α异号，从而可判断角α为第二或第三象限角．
由eq \f(cs α,tan α)＜0可知cs α，tan α异号，从而可判断角α为第三或第四象限角．
综上可知，角α为第三象限角．
(2)sin 2＞0，cs 3＜0，tan 4＞0，则sin 2·cs 3·tan 4＜0，故选A.]
►考法3 三角函数线的应用
【例4】 函数y＝eq \r(,2cs x－1)的定义域为________．
eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,3)，2kπ＋\f(π,3)))(k∈Z)
[∵2cs x－1≥0，
∴cs x≥eq \f(1,2).
由三角函数线画出x满足条件的终边范围(如图阴影所示)．
∴x∈eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,3)，2kπ＋\f(π,3)))(k∈Z)．]
[规律方法] 1.利用三角函数定义求三角函数值的方法
(1)已知角α终边上一点P的坐标，则可先求出点P到原点的距离r，然后用三角函数的定义求解．
(2)已知角α的终边所在的直线方程，则可先设出终边上一点的坐标，求出此点到原点的距离，然后用三角函数的定义求解．
2．利用三角函数线求解三角不等式的方法
对于较为简单的三角不等式，在单位圆中，利用三角函数线先作出使其相等的角(称为临界状态，注意实线与虚线)，再通过大小找到其所满足的角的区域，由此写出不等式的解集．
(1)点P从(1,0)出发，沿单位圆逆时针方向运动eq \f(2π,3)弧长到达Q点，则Q点的坐标为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)，\f(\r(3),2))) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，－\f(1,2)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)，－\f(\r(3),2))) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),2)，\f(1,2)))
(2)若角θ的终边经过点P(－eq \r(3)，m)(m≠0)且sin θ＝eq \f(\r(2),4)m，则cs θ的值为________．
(3)函数y＝lg(2sin x－1)的定义域为________．
(1)A (2)－eq \f(\r(6),4) (3)eq \b\lc\(\rc\)(\a\vs4\al\c1(2kπ＋\f(π,6)，2kπ＋\f(5,6)π))k∈Z [(1)由三角函数定义可知Q点的坐标(x，y)满足x＝cs eq \f(2π,3)＝－eq \f(1,2)，y＝sin eq \f(2π,3)＝eq \f(\r(3),2).
∴Q点的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)，\f(\r(3),2)))，故选A.
(2)由题意知r＝eq \r(3＋m2)，
∴sin θ＝eq \f(m,\r(3＋m2))＝eq \f(\r(2),4)m，
∵m≠0，∴m＝±eq \r(5)，∴r＝eq \r(3＋m2)＝2eq \r(2)，
∴cs θ＝eq \f(－\r(3),2\r(2))＝－eq \f(\r(6),4).
(3)由题意知2sin x－1＞0，即sin x＞eq \f(1,2)，
根据三角函数线，画出x满足条件的终边范围．(如图阴影所示)
∴eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(2kπ＋\f(π,6)＜x＜2kπ＋\f(5π,6)，k∈Z))))
1．(2014·全国卷Ⅰ)若tan α>0，则( )
A．sin 2α>0 B．cs α>0
C．sin α>0 D．cs 2α>0
A [∵tan α>0，∴α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ，kπ＋\f(π,2)))(k∈Z)是第一、三象限角．
∴sin α，cs α都可正、可负，排除B，C.
而2α∈(2kπ，2kπ＋π)(k∈Z)，
结合正、余弦函数图象可知，A正确．
取α＝eq \f(π,4)，则tan α＝1>0，而cs 2α＝0，故D不正确．]
2．(2014·大纲全国卷)已知角α的终边经过点(－4,3)，则cs α＝( )
A．eq \f(4,5) B．eq \f(3,5)
C．－eq \f(3,5) D．－eq \f(4,5)
D [因为角α的终边经过点(－4,3)，所以x＝－4，y＝3，r＝5，所以cs α＝eq \f(x,r)＝－eq \f(4,5).]角α的弧度数公式
|α|＝eq \f(l,r)(弧长用l表示)
角度与弧度的换算
①1°＝eq \f(π,180) rad；
②1 rad＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(180,π)))°
弧长公式
弧长l＝|α|r
扇形面积公式
S＝eq \f(1,2)lr＝eq \f(1,2)|α|r2
三角函数
正弦
余弦
正切
定义
设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么
y叫做α的正弦，记作sin α
x叫做α的余弦，记作cs α
eq \f(y,x)叫做α的正切，记作tan α
三角函数线
有向线段MP为正弦线
有向线段OM为余弦线
有向线段AT为正切线
象限角与终边相同的角
扇形的弧长、面积公式
三角函数的定义