

高考数学一轮复习教案 第3章_第2节_同角三角函数的基本关系与诱导公式(含答案解析)
展开第二节 同角三角函数的基本关系与诱导公式
[考纲传真] 1.理解同角三角函数的基本关系式:sin2α+cos2α=1,=tan α.2.能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式.

1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1;
(2)商数关系:tan α=.
2.诱导公式
组序 | 一 | 二 | 三 | 四 | 五 | 六 |
角 | 2kπ+ α(k∈Z) | π+α | -α | π-α | -α | +α |
正弦 | sin α | -sin α | -sin α | sin α | cos α | cos_α |
余弦 | cos α | -cos α | cos α | -cos_α | sin α | -sin α |
正切 | tan α | tan α | -tan α | -tan_α |
|
|
口诀 | 函数名不变,符号看象限 | 函数名改变 符号看象限 | ||||
同角三角函数的基本关系式的几种变形
(1)(sin α±cos α)2=1±2sin αcos α.
(2)sin2α=1-cos2α=(1+cos α)(1-cos α).
(3)cos2α=1-sin2α=(1+sin α)(1-sin α).
(4)sin α=tan αcos α.
[基础自测]
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)若α,β为锐角,则sin2α+cos2β=1. ( )
(2)若α∈R,则tan α=恒成立. ( )
(3)sin(π+α)=-sin α成立的条件是α为锐角. ( )
(4)若sin(kπ-α)=(k∈Z),则sin α=. ( )
[答案] (1)× (2)× (3)× (4)×
2.(教材改编)已知α是第二象限角,sin α=,则cos α等于( )
A.- B.- C. D.
B [∵sin α=,α是第二象限角,
∴cos α=-=-.]
3.sin 750°=________.
[sin 750°=sin(2×360°+30°)=sin 30°=.]
4.已知sin=,α∈,则sin(π+α)=________.
- [因为sin=cos α=,α∈,所以sin α==,所以sin(π+α)=-sin α=-.]
5.(教材改编)已知tan α=2,则的值为________.
[===.]

| 同角三角函数关系的应用 |
![]()
1.若α是三角形的内角,且tan α=-,则sin α+cos α的值为( )
A. B.
C.- D.-
C [由tan α=-,得sin α=-cos α,将其代入sin2α+cos2α=1,
得cos2α=1,∴cos2α=,易知cos α<0,
∴cos α=-,sin α=,
故sin α+cos α=-.]
2.(2019·合肥模拟)已知tan α=-,则sin α(sin α-cos α)=( )
A. B. C. D.
A [sin α(sin α-cos α)=sin2α-sin αcos α==,将tan α=-代入,
得原式==,故选A.]
3.已知sin αcos α=,且<α<,则cos α-sin α的值为( )
A.- B. C.- D.
B [∵<α<,
∴cos α<0,sin α<0且cos α>sin α,
∴cos α-sin α>0.
又(cos α-sin α)2=1-2sin αcos α=1-2×=,
∴cos α-sin α=,故选B.]
4.已知sin θ+cos θ=,θ∈,则sin θ-cos θ的值为( )
A. B.- C. D.-
B [因为(sin θ+cos θ)2=sin2θ+cos2θ+2sin θ·cos θ=1+2sin θcos θ=,所以2sin θcos θ=,则(sin θ-cos θ)2=sin2θ+cos2θ-2sin θ·cos θ=1-2sin θcos θ=.又因为θ∈,所以sin θ<cos θ,
即sin θ-cos θ<0,
所以sin θ-cos θ=-,故选B.]
[规律方法] 同角三角函数关系式及变形公式的应用方法
1利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用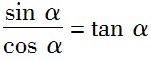 可以实现角α的弦切互化.
可以实现角α的弦切互化.
2应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用sin α±cos α2=1±2sin αcos α,可以知一求二.
3注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
| 诱导公式的应用 |
![]()
【例1】 (1)sin(-1 200°)cos 1 290°=________.
(2)已知cos=a,则cos+sin=________.
(3)已知A=+(k∈Z),则A的值构成的集合是________.
(1) (2)0 (3){2,-2} [(1)原式=-sin 1 200°cos 1290°
=-sin(3×360°+120°)cos(3×360°+210°)
=-sin 120°cos 210°
=-sin(180°-60°)cos(180°+30°)
=sin 60°cos 30°=×=.
(2)cos=cos=-cos=-a,sin=sin=cos=a
∴cos+sin=-a+a=0.
(3)当k为偶数时,A=+=2;k为奇数时,A=-=-2,因此A的值构成的集合为{2,-2} .]
[规律方法] 1.诱导公式用法的一般思路
(1)化负为正,化大为小,化到锐角为止.
(2)角中含有加减的整数倍时,用公式去掉的整数倍.
2.常见的互余和互补的角
(1)常见的互余的角:-α与+α;+α与-α;+α与-α等.
(2)常见的互补的角:+θ与-θ;+θ与-θ等.
3.三角函数式化简的方向
(1)切化弦,统一名.
(2)用诱导公式,统一角.
(3)用因式分解将式子变形,化为最简.
![]() (1)已知α∈,且cos α=-,则=( )
(1)已知α∈,且cos α=-,则=( )
A. B.-
C. D.-
(2)已知sin=,则cos=________.
(1)C (2) [(1)===,
又α∈,cos α=-,则sin α=,
从而==,故选C.
(2)因为+=.
所以cos=cos
=sin=.]
| 同角三角函数的基本关系式与诱导公式的综合应用 |
![]()
【例2】 (1)(2016·全国卷Ⅰ)已知θ是第四象限角,且sin=,则tan=________.
(2)已知cos=2sin,则的值为________.
(1)- (2) [(1)由题意知sin=,θ是第四象限角,所以cos>0,所以cos==.
sin=sin=cos=,
cos=cos=sin=.
∴tan=-tan=-.
(2)∵cos=2sin,
∴-sin α=-2cos α,
则sin α=2cos α,
代入sin2α+cos2α=1,
得cos2α=.
=
==cos2α-=.]
[规律方法] 化简三角函数式的基本思路和要求
1基本思路,①分析结构特点,选择恰当公式;②利用公式化成单角三角函数;③整理得最简形式.
2化简要求:①化简过程是恒等变形;②结构要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.
![]() (1)(2019·唐山模拟)已知sin=,那么tan α的值为( )
(1)(2019·唐山模拟)已知sin=,那么tan α的值为( )
A.- B.- C.± D.±
(2)设f(α)=(1+2sin α≠0),则f=________.
(1)C (2) [sin=sin=cos α=,
则sin α=±,所以tan α==±,故选C.
(2)因为f(α)=
===,
所以f=
===.]

![]() 1.(2017·全国卷Ⅲ)已知sin α-cos α=,则sin 2α=( )
1.(2017·全国卷Ⅲ)已知sin α-cos α=,则sin 2α=( )
A.- B.- C. D.
A [∵sin α-cos α=,
∴(sin α-cos α)2=1-2sin αcos α=1-sin 2α=,
∴sin 2α=-.
故选A.]
2.(2016·全国卷Ⅲ)若tan θ=-,则cos 2θ=( )
A.- B.- C. D.
D [∵cos 2θ==
又∵tan θ=-,∴cos 2θ==.]
![]() 3.(2016·全国卷Ⅲ)若tan α=,则cos2α+2sin 2α=( )
3.(2016·全国卷Ⅲ)若tan α=,则cos2α+2sin 2α=( )
A. B. C.1 D.
A [因为tan α=,则cos2α+2sin 2α====.故选A.]
新高考数学一轮复习讲练教案4.2 同角三角函数的基本关系与诱导公式(含解析): 这是一份新高考数学一轮复习讲练教案4.2 同角三角函数的基本关系与诱导公式(含解析),共13页。
高中数学高考第二节 同角三角函数的基本关系与诱导公式 教案: 这是一份高中数学高考第二节 同角三角函数的基本关系与诱导公式 教案,共13页。
高中数学高考第2节 同角三角函数的基本关系与诱导公式 教案: 这是一份高中数学高考第2节 同角三角函数的基本关系与诱导公式 教案,共10页。












