高考数学一轮复习教案 第7章_第3节_空间点、直线、平面之间的位置关系(含答案解析)
展开第三节 空间点、直线、平面之间的位置关系
[考纲传真] 1.理解空间直线、平面位置关系的定义.2.了解可以作为推理依据的公理和定理.3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.

1.平面的基本性质
(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在这个平面内.
(2)公理2:过不在一条直线上的三点,有且只有一个平面.
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
(4)公理2的三个推论
推论1:经过一条直线和这条直线外的一点,有且只有一个平面.
推论2:经过两条相交直线,有且只有一个平面.
推论3:经过两条平行直线,有且只有一个平面.
2.空间直线的位置关系
(1)位置关系的分类
(2)异面直线所成的角
①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).
②范围:.
(3)平行公理(公理4)和等角定理
平行公理:平行于同一条直线的两条直线互相平行.
等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
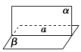
3.空间中直线与平面、平面与平面的位置关系
(1)空间中直线与平面的位置关系
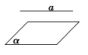
位置关系 | 图形表示 | 符号表示 | 公共点 | |
直线a在平面α内 |
| a⊂α | 有无数个公共点 | |
直线在平面外 | 直线a平面α平行 |
| a∥α | 没有公共点 |
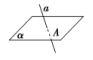
直线a与平面α斜交 |
| a∩α=A | 有且只有一个公共点 | |
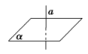
直线a与平面α垂直 |
| a⊥α | ||
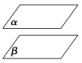
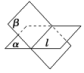
(2)空间中两个平面的位置关系
位置关系 | 图形表示 | 符号表示 | 公共点 | |
两平面平行 |
| α∥β | 没有 公共点 | |
两平面相交 | 斜交 |
| α∩β=l | 有一条 公共 直线 |
垂直 |
| α⊥β且 α∩β=a | ||
1.异面直线的判定定理
经过平面内一点的直线与平面内不经过该点的直线互为异面直线.
2.等角定理的引申
(1)在等角定理中,若两角的两边平行且方向相同或相反,则这两个角相等.
(2)在等角定理中,若两角的两边平行且方向一个边相同,一个边相反,则这两个角互补.
[基础自测]
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)两个平面α,β有一个公共点A,就说α,β相交于过A点的任意一条直线. ( )
(2)两两相交的三条直线最多可以确定三个平面. ( )
(3)如果两个平面有三个公共点,则这两个平面重合. ( )
(4)若直线a不平行于平面α,且a⊄α,则α内的所有直线与a异面.( )
[答案] (1)× (2)√ (3)× (4)×
2.(教材改编)如图所示,在正方体ABCDA1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小为( )
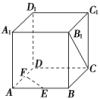
A.30° B.45°
C.60° D.90°
C [连接B1D1,D1C(图略),则B1D1∥EF,故∠D1B1C为所求的角,又B1D1=B1C=D1C,
∴∠D1B1C=60°.]
3.(教材改编)下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
D [根据确定平面的公理和推论知选项D正确.]
4.已知空间四边形的两条对角线相互垂直,顺次连接四边中点的四边形 一定是( )
A.空间四边形 B.矩形
C.菱形 D.正方形
B [四边形的相邻两边分别平行于空间四边形的两角对角线,故选B.]
5.已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A [由题意知a⊂α,b⊂β,若a,b相交,则a,b有公共点,从而α,β有公共点,可得出α,β相交;反之,若α,β相交,则a,b的位置关系可能为平行、相交或异面.因此“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件.故选A.]

| 平面的基本性质 |
【例1】 (1)以下命题中,正确命题的个数是( )
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
A.0 B.1 C.2 D.3
B [①正确,可以用反证法证明,假设任意三点共线,则四个点必共面,与不共面的四点矛盾;②中若点A,B,C在同一条直线上,则A,B,C,D,E不一定共面,故②错误;③中,直线b,c可能是异面直线,故③错误;④中,当四条线段构成空间四边形时,四条线段不共面,故④错误.]
(2)如图,正方体ABCDA1B1C1D1中,E,F分别是AB和AA1的中点.求证:
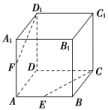
①E,C,D1,F四点共面;
②CE,D1F,DA三线共点.
[解] ①如图,连接EF,CD1,A1B.
∵E,F分别是AB,AA1的中点,
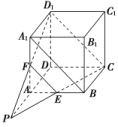
∴EF∥BA1.
又∵A1B∥D1C,∴EF∥CD1,
∴E,C,D1,F四点共面.
②∵EF∥CD1,EF<CD1,
∴CE与D1F必相交,设交点为P,
则由P∈直线CE,CE⊂平面ABCD,
得P∈平面ABCD.
同理P∈平面ADD1A1.
又平面ABCD∩平面ADD1A1=DA,
∴P∈直线DA,∴CE,D1F,DA三线共点.
[规律方法] 共点、共线、共面问题的证明方法
1证明点共线问题:①公理法:先找出两个平面,然后证明这些点都是这两个平面的公共点,再根据基本公理3证明这些点都在交线上;②同一法:选择其中两点确定一条直线,然后证明其余点也在该直线上.
2证明线共点问题:先证两条直线交于一点,再证明第三条直线经过该点.
3证明点、直线共面问题:①纳入平面法:先确定一个平面,再证明有关点、线在此平面内;②辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面α,β重合.
![]() (1)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是 ( )
(1)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是 ( )
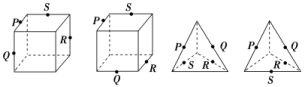
A B C D
D [根据异面直线的判定定理,选项D中PS与QR是异面直线,则四点P,Q,R,S不共面.故选D.]
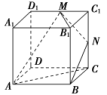
(2)如图,在正方体ABCDA1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点.求证:D1,H,O三点共线.
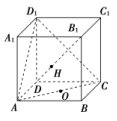
[证明] 如图,连接BD,B1D1,
则BD∩AC=O,
因为BB1DD1,
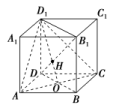
所以四边形BB1D1D为平行四边形,
又H∈B1D,
B1D⊂平面BB1D1D,
则H∈平面BB1D1D,
因为平面ACD1∩平面BB1D1D=OD1,
所以H∈OD1.
即D1,H,O三点共线.
| 空间两条直线的位置关系 |
![]()
【例2】 (1)已知a,b,c为三条不同的直线,且a⊂平面α,b⊂平面β,α∩β=c,给出下列命题:
①若a与b是异面直线,则c至少与a,b中的一条相交;
②若a不垂直于c,则a与b一定不垂直;
③若a∥b,则必有a∥c.
其中真命题有________.(填序号)
(2)在图中,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有________(填上所有正确答案的序号).
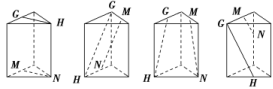
① ② ③ ④
(1)①③ (2)②④ [(1)对于①,若c与a,b都不相交,则c∥a,c∥b,从而a∥b,这与a与b是异面直线矛盾,故①正确.
对于②,a与b可能异面垂直,故②错误.
对于③,由a∥b可知a∥β,又α∩β=c,从而a∥c,故③正确.
(2)图①中,直线GH∥MN;图②中,G,H,N三点共面,但M∉平面GHN,因此直线GH与MN异面;图③中,连接MG(图略),GM∥HN,因此GH与MN共面;图④中,G,M,N共面,但H∉平面GMN,因此GH与MN异面,所以在图②④中,GH与MN异面.]
[规律方法] 异面直线的判定方法

![]() (1)已知a,b是异面直线,直线c平行于直线a,那么c与b( )
(1)已知a,b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线 B.一定是相交直线
C.不可能是平行直线 D.不可能是相交直线
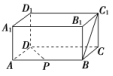
(2)如图所示,正方体ABCDA1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为________.(把你认为正确的结论的序号都填上)
(1)C (2)③④ [(1)c与b可能相交,也可能异面,但可不能平行,故选C.
(2)根据两条异面直线的判定定理知,③④正确.]
| 异面直线所成的角 |
![]() 【例3】 (1)(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )
【例3】 (1)(2018·全国卷Ⅱ)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )
A. B. C. D.
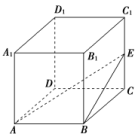
(2)如图,在长方体ABCDA1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成的角等于( )
A.30° B.45° C.60° D.90°
(1)C (2)C [(1)如图,连接BE,
因为AB∥CD,所以异面直线AE与CD所成的角等于相交直线AE与AB所成的角,即∠EAB.不妨设正方体的棱长为2,则CE=1,BC=2,由勾股定理得BE=.又由AB⊥平面BCC1B1可得AB⊥BE,所以tan∠EAB==.故选C.
(2)取CD的中点Q,连接BQ,C1Q
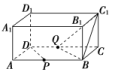
∵P是AB的中点,
∴BQ∥PD
∴∠C1BQ是异面直线BC1与PD所成的角.
在△C1BQ中,C1B=BQ=C1Q=,
∴∠C1BQ=60°,
即异面直线BC1与PD所成的角等于60°,故选C.]
[规律方法] 用平移法求异面直线所成的角的步骤
1一作:根据定义作平行线,作出异面直线所成的角;
2二证:证明作出的角是异面直线所成的角;
3三求:解三角形,求出作出的角.如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角.
![]() (1)已知P是△ABC所在平面外的一点,M,N分别是AB、PC的中点,若MN=BC=4,PA=4,则异面直线PA与MN所成角的大小是( )
(1)已知P是△ABC所在平面外的一点,M,N分别是AB、PC的中点,若MN=BC=4,PA=4,则异面直线PA与MN所成角的大小是( )
A.30° B.45°
C.60° D.90°
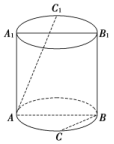
(2)如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为________.
(1)A (2) [(1)取AC的中点O,连接OM,ON,则
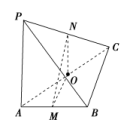
OMBC,ONPA.
∴∠ONM就是异面直线PA与MN所成的角.
在△OMN中,MN=4,OM=2,ON=2,
∴cos∠ONM===,
∴∠ONM=30°
即异面直线PA与MN所成角的大小为30°,故选A.
(2)取圆柱下底面弧AB的另一中点D,连接C1D,AD,
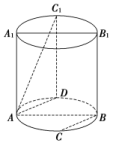
因为C是圆柱下底面弧AB的中点,所以AD∥BC,
所以直线AC1与AD所成角等于异面直线AC1与BC所成角,因为C1是圆柱上底面弧A1B1的中点,所以C1D⊥圆柱下底面,所以C1D⊥AD.
因为圆柱的轴截面ABB1A1是正方形,所以C1D=AD,所以直线AC1与AD所成角的正切值为,所以异面直线AC1与BC所成角的正切值为.]

![]()
1.(2017·全国卷Ⅱ)已知直三棱柱ABCA1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A. B.
C. D.
C [将直三棱柱ABCA1B1C1补形为直四棱柱ABCDA1B1C1D1,如图所示,连接AD1,B1D1,BD.
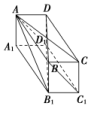
由题意知∠ABC=120°,AB=2,BC=CC1=1,
所以AD1=BC1=,AB1=,∠DAB=60°.
在△ABD中,由余弦定理知BD2=22+12-2×2×1×cos 60°=3,所以BD=,所以B1D1=.
又AB1与AD1所成的角即为AB1与BC1所成的角θ,
所以cos θ===.
故选C.]
2.(2016·全国卷Ⅰ)平面α过正方体ABCDA1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A. B. C. D.
A [根据平面与平面平行的性质,将m,n所成的角转化为平面CB1D1与平面ABCD的交线及平面CB1D1与平面ABB1A1的交线所成的角.
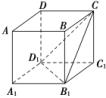
设平面CB1D1∩平面ABCD=m1.∵平面α∥平面CB1D1,∴m1∥m.
又平面ABCD∥平面A1B1C1D1,
且平面CB1D1∩平面A1B1C1D1=B1D1,
∴B1D1∥m1.∴B1D1∥m.
∵平面ABB1A1∥平面DCC1D1,且平面CB1D1∩平面DCC1D1=CD1,同理可证CD1∥n.
因此直线m与n所成的角即直线B1D1与CD1所成的角.
在正方体ABCDA1B1C1D1中,△CB1D1是正三角形,
故直线B1D1与CD1所成角为60°,其正弦值为.]
新高考数学一轮复习讲练教案7.2 空间点、直线、平面之间的位置关系(含解析): 这是一份新高考数学一轮复习讲练教案7.2 空间点、直线、平面之间的位置关系(含解析),共17页。
高考数学一轮复习教案7.2《空间点、直线、平面之间的位置关系》教案及课后作业(4份打包,原卷版+教师版): 这是一份高考数学一轮复习教案7.2《空间点、直线、平面之间的位置关系》教案及课后作业(4份打包,原卷版+教师版),文件包含高考数学一轮复习教案72《空间点直线平面之间的位置关系》教案教师版pdf、高考数学一轮复习教案72《空间点直线平面之间的位置关系》教案原卷版pdf、高考数学一轮复习教案72《空间点直线平面之间的位置关系》课后作业教师版pdf、高考数学一轮复习教案72《空间点直线平面之间的位置关系》课后作业原卷版pdf等4份教案配套教学资源,其中教案共28页, 欢迎下载使用。
高中数学高考第3节 空间点、直线、平面之间的位置关系 教案: 这是一份高中数学高考第3节 空间点、直线、平面之间的位置关系 教案,共12页。