2023-2024学年九年级（上）第21章 一元二次方程 章末检测卷

这是一份2023-2024学年九年级（上）第21章 一元二次方程 章末检测卷，共7页。
2023-2024学年九年级（上）第21章 一元二次方程 章末检测卷一．选择题（共10小题，满分30分，每小题3分）1．下列方程是一元二次方程的是（　　）A．5（x﹣1）＝3x B．+x2＝0 C．3x2﹣x＝0 D．x（x﹣1）＝y2．关于x的一元二次方程x2＝5x﹣1的二次项系数、一次项系数、常数项分别是（　　）A．1，﹣5，﹣1 B．﹣1，﹣5，﹣1 C．1，﹣5，1 D．1，5，13．若方程x2+kx﹣3＝0有一个根是1，则另一个根是（　　）A．1 B． C．﹣3 D．24．将方程3x2﹣9x+2＝0配方成（x+m）2＝n的形式为（　　）A． B． C．（x﹣3）2＝ D．5．若关于x的方程x2﹣2x+k﹣1＝0有实数根，则k的取值不可以是（　　）A．0 B．1 C．2 D．36．某公司去年10月份的营业额为2500万元，后来公司改变营销策略，12月份的营业额达到3780万元，已知12月份的增长率是11月份的1.3倍，求11月份的增长率，设11月份的增长率为x，根据题意，可列方程为（　　）A．2500（1+x）（1+1.3x）＝3780 B．2500（1+x）2＝3780 C．2500（1+1.3x）2＝3780 D．2500（1+2.3x）＝37807．有一人患了流感，经过两轮传染后共有169人患了流感，设每轮传染中平均一个人传染了x人，则x的值为（　　）A．11 B．12 C．13 D．148．已知实数m，n满足（m2+n2）2﹣2（m2+n2）＝3，则m2+n2的值为（　　）A．3 B．﹣1 C．﹣1或3 D．﹣3或19．已知m、n是一元二次方程x2+x﹣2023＝0的两个实数根，则代数式m2+2m+n的值等于（　　）A．2019 B．2020 C．2021 D．202210．对于两个不相等的实数a，b，我们规定符号max（a，b）表示a，b中的较大值，如：max（3，5）＝5，因此，max（﹣3，﹣5）＝﹣3：按照这个规定，若max{x，﹣x}＝x2﹣3x﹣5，则x的值是（　　）A．5 B．5或 C．﹣1或 D．5或二．填空题（共6小题，满分18分，每小题3分）11．当a＝　   　时，xa﹣1﹣5x＝3是关于x的一元二次方程．12．若关于x的一元二次方程x2﹣6x+k＝0有两个不相等的实数根，则k的取值范围是 　      　．13．某单位要组织一次篮球比赛，赛制为单循环形式（每两队之间只赛一场），计划安排36场比赛，应邀请 　   　支球队参加比赛．14．新园小区计划在一块长为40米，宽为26米的矩形场地上修建三条同样宽的甬路（两条纵向、一条横向，且横向、纵向互相垂直），其余部分种花草．若要使种花草的面积达到800m2，则甬路宽为多少米？设甬路宽为x米，则根据题意，可列方程为　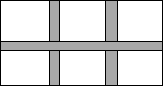                  　．15．若菱形两条对角线的长度是方程x2﹣9x+20＝0的两根，则该菱形的面积为 　     　．16．已知一元二次方程x2﹣4x﹣3＝0的两根分别为m，n，则的值为　                 　．三．解答题（共6小题，满分52分）17．（8分）解方程：（1）x2﹣4x+5＝0；                 （2）（x+2）2﹣3（x+2）＝0．    18．（8分）已知关于x的一元二次方程（a+c）x2﹣2bx+（a﹣c）＝0，其中a、b、c分别为△ABC三边的长．（1）如果x＝1是方程的根，试判断△ABC的形状，并说明理由；（2）如果△ABC是等边三角形，试求这个一元二次方程的根．    19．（8分）已知关于x的一元二次方程（x﹣1）（x﹣2k）+k（k﹣1）＝0．（1）求证：该一元二次方程总有两个不相等的实数根；（2）若该方程的两个根x1，x2是一个矩形的一边长和对角线的长，且矩形的另一边长为5，试求k的值．    20．（9分）某商店销售一种商品，每件的进价为20元．根据市场调查，当售价不低于30元/件时，这种商品销售量y（件）与售价x（元/件）之间的函数关系的部分图象如图所示．（1）求y关于x的函数解析式；（不要写自变量取值范围）（2）商店销售这种商品是否能获得1080元利润？如果可以，求出该商品销售单价；如果不行，请说明理由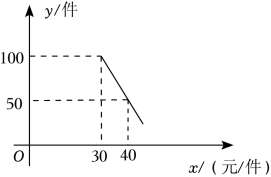．    21．（9分）提出问题：为解方程（x2﹣2）2﹣11（x2﹣2）+18＝0，我们可以将x2﹣2视为一个整体，然后可设x2﹣2＝y，则（x2﹣2）2＝y2，于是原方程可转化为y2﹣11y+18＝0，解此方程，得y1＝2，y2＝9．当y1＝2时，x2﹣2＝2，x2＝4，∴x＝±2；当y2＝9时，x2﹣2＝9，x2＝11，∴．∴原方程的解为x1＝2，x2＝﹣2，，．以上方法就是换元法解方程，从而达到了降次的目的，体现了转化的思想．解决问题：（1）运用上述换元法解方程x4﹣3x2﹣4＝0．延伸拓展：（2）已知实数m，n满足（m+3n）（m+3n﹣2）＝2m+6n﹣4，求4m+12n﹣3的值．       22．（10分）如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝8cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始沿BC边向点C以2cm/s的速度移动，当其中一点到达终点时，另外一点也随之停止运动．（1）几秒后，四边形APQC的面积等于16cm2？（2）△PQB的面积能否等于9cm2？请说明理由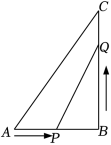．                 参考答案一．选择题1．C．2．C．3．C．4．A．5．D．6．A．7．B．8．A．9．D．10．B．二．填空题11．3．   12．k＜9．   13．9．   14．（40﹣2x）（26﹣x）＝800．   15．10．   16．﹣．三．解答题17．解：（1）x2﹣4x+5＝0，配方得：x2﹣4x+4＝﹣5+4，即（x﹣2）2＝﹣1，∴方程没有实数根；（2）（x+2）2﹣3（x+2）＝0，（x+2）（x+2﹣3）＝0，x+2＝0或x+2﹣3＝0，解得：x1＝﹣2，x2＝1．18．解：（1）△ABC是等腰三角形，理由是：∵把x＝1代入方程（a+c）x2﹣2bx+（a﹣c）＝0得：a+c﹣2b+a﹣c＝0，∴2a＝2b，∴a＝b，∴△ABC的形状是等腰三角形； （2）∵△ABC是等边三角形，∴a＝b＝c，∵（a+c）x2﹣2bx+（a﹣c）＝0，∴（a+a）x2﹣2ax+a﹣a＝0，即x2﹣x＝0，解得：x1＝0，x2＝1，即这个一元二次方程的根是x1＝0，x2＝1．19．解：（1）（x﹣1）（x﹣2k）+k（k﹣1）＝0，整理得：x2﹣（2k+1）x+k2+k＝0，∵a＝1，b＝﹣（2k+1），c＝k2+k，∴Δ＝b2﹣4ac＝（2k+1）2﹣4×1×（k2+k）＝1＞0；∴该一元二次方程总有两个不相等的实数根；（2）x2﹣（2k+1）x+k2+k＝0，∴x1＝k，x2＝k+1，∵x2＝k+1＞k＝x1，∴x2＝k+1为对角线，（k+1）2＝k2+52，解得：k＝12．20．解：（1）设y与x之间的函数解析式为y＝kx+b（k≠0），根据函数图象知，该直线经过点（30，100），（40，50），将其分别代入y＝kx+b，得，解得．即：y与x之间的函数解析式为y＝﹣5x+250；（2）若商店销售这种商品能获得1080元利润，则（x﹣20）（﹣5x+250）＝1080，解得x1＝32，x2＝38．答：商店销售这种商品能获得1080元利润，销售单价为32元或38元．21．解：（1）设x2＝y，则原方程可转化为y2﹣3y﹣4＝0，解得：y1＝4，y2＝﹣1，当y1＝4时，x2＝4，∴x＝±2；当y2＝﹣1，x2＝﹣1，此方程无解．∴原方程的解为x1＝2，x2＝﹣2；（2）∵（m+3n）（m+3n﹣2）＝2m+6n﹣4，∴（m+3n）（m+3n﹣2）＝2（m+3n）﹣4，设m+3n＝t，则t（t﹣2）＝2t﹣4，整理得：t2﹣4t+4＝（t﹣2）2＝0，解得：t＝2，∴m+3n＝2，∴4m+12n﹣3＝4（m+3n）﹣3＝4×2﹣3＝5．22．解：（1）经过x秒钟，四边形APQC的面积等于16cm2，∵在△ABC中，∠B＝90°，AB＝5cm，BC＝8cm．∴∴，∵点P从点A开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始沿BC边向点C以2cm/s的速度移动，∴BP＝AB﹣AP＝5﹣x，BQ＝2x，∴，∴x2﹣5x+4＝0，解得x＝1或x＝4（舍去），∴经过1秒钟，四边形APQC的面积等于16cm2；（2）△PQB的面积不能等于9cm2，理由如下：同（1）得，∴x2﹣5x+9＝0，∵Δ＝b2﹣4ac＝（﹣5）2﹣4×9×1＝﹣11＜0，∴此方程无解，∴△PQB的面积不能等于9cm2．