人教版2023-2024学年九年级（上）第21章《一元二次方程》达标检测卷 含答案

人教版2023-2024学年九年级（上）第21章《一元二次方程》达标检测卷

一．选择题（共10小题，满分30分，每小题3分）

1．下列方程是关于x的一元二次方程的是（　　）

A．ax2+bx+c＝0 B． C．x2+2x＝x2﹣1 D．3（x+1）2＝﹣3

2．一元二次方程x2+mx＝2的一个根为2，则m的值为（　　）

A．1 B．2 C．﹣1 D．﹣2

3．用配方法将方程x2﹣4x+3＝0化成（x﹣a）2＝b的形式，则a﹣b的值是（　　）

A．1 B．﹣1 C．3 D．﹣3

4．若关于x的一元二次方程kx2﹣x﹣1＝0有实数根，则实数k的取值范围是（　　）

A． B． C． D．

5．方程x2+10x+9＝0的两个根是（　　）

A．x1＝1，x2＝9 B．x1＝﹣1，x2＝9 

C．x1＝1，x2＝﹣9 D．x1＝﹣1，x2＝﹣9

6．已知关于x的一元二次方程x2﹣2x+b+2＝0有两个不相等的实数根，则一次函数y＝x+b的图象一定不经过（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限​

7．实数a，b，c满足a﹣b+c＝0，则（　　）

A．b2﹣4ac＞0 B．b2﹣4ac＜0 C．b2﹣4ac≥0 D．b2﹣4ac≤0

8．已知关于x的方程x2+px+q＝0的两根为﹣3和2，则的值为（　　）

A．﹣6 B． C． D．6

9．已知x，y为实数，且满足x2﹣xy+4y2＝4，记u＝x2+xy+4y2的最大值为M，最小值为m，则M+m＝（　　）

A． B． C． D．

10．定义[x]表示不超过实数x的最大整数，如[1.4]＝1，[﹣1.2]＝﹣2，[﹣3]＝﹣3，则方程2[x]＝x2的解为（　　）

A．0或 B．0或2 C．2或 D．0或或2

二．填空题（共7小题，满分21分，每小题3分）

11．已知2x|m|﹣2+3＝9是关于x的一元二次方程，则m＝　     　．

12．一元二次方程3x2﹣4x﹣1＝0的二次项系数是 　   　，一次项系数是 　     　．

13．一元二次方程x2+4x＝0根的判别式的值为 　     　．

14．两个奇数，其中一个为另一个的平方，较大奇数与较小奇数的差为110，两个奇数分别为 　     　，　      　．

15．定义运算：a&b＝ab2﹣ab+1．例如：4&2＝4×22﹣4×2+1．若关于x的方程2&x＝m有两个相等的实数根，则m的值为 　                　．

16．用一段长为30m的篱笆围成一个靠墙的矩形菜园，若菜园的面积为100m2，墙的长度为18m．设垂直于墙的一边长为xm，则x的值为 　     　．

17．已知m，n是方程x2+2x﹣3＝0的两个根，则＝　                　．

三．解答题（共10小题，满分69分）

18．（6分）用适当的方法解下列方程；

（1）2x2+4x﹣1＝0；

（2）x2﹣8x﹣20＝0．

19．（6分）方程x2+2x+m﹣1＝0是关于x的一元二次方程，该方程的两个实数根分别为x1，x2．

（1）求m的取值范围；

（2）若++3x1x2+10＝0，求m的值．

20．（6分）区教育局要组织辖区内学校进行足球友谊赛，赛制为单循环形式，即每两所学校之间都赛一场，计划安排28场比赛，应邀请多少所学校参加比赛？

21．（6分）某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分枝，主干，支干和小分枝的总数是73，每个支干长出多少分枝？

22．（6分）如图，有一块长为30米，宽为20米的矩形场地，计划在该场地上修建两条

互相垂直的小道，横向小道与竖向小道的宽比为2：3，余下矩形场地建成草坪，草坪的面积为486平方米，请求出横向小道的宽．

23．（7分）将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和，这种方法称之为配方法．这种方法常常被用到式子的恒等变形中，以挖掘题目中的隐含条件，是解题的有力手段之一．

例如，求代数式x2+2x+3的最小值

解：原式＝x2+2x+1+2＝（x+1）2+2．

∵（x+1）2≥0，

∴（x+1）2+2≥2．

∴当x＝﹣1时，x2+2x+3的最小值是2．

（1）请仿照上面的方法求代数式x2+6x﹣1的最小值．

（2）已知△ABC的三边a，b，c满足a2﹣6b＝﹣14，b2﹣8c＝﹣23，c2﹣4a＝8．求△ABC的周长．

24．（7分）我市某超市于今年年初以每件30元的进价购进一批商品．当商品售价为40元时，一月份销售250件．二、三月该商品十分畅销．销售量持续走高．在售价不变的基础上，三月底的销售量达到360件．设二、三这两个月的月平均增长率不变．

（1）求二、三这两个月的月平均增长率；

（2）从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价1元，销售量增加6件，当商品降价多少元时，商场获利1950元？

25．（8分）如果方程x2+px+q＝0满足两个实数解都为整数解，我们就称所有这样的一元二次方程为同族方程，并规定：满足G＝，例如x2﹣7x+12＝0有整数解3和4，所以x2﹣7x+12＝0属于同族方程，所以G＝＝．

（1）如果同族方程x2+px+q＝0中有两个相等的解，我们称这个方程为同族方程中的完美方程，求证：对任意一个完美方程，总有G＝4；

（2）关于x的一元二次方程kx2﹣（k﹣3）x﹣3＝0属于同族方程，求整数k的值．

26．（8分）阅读下面的材料：

解方程x4﹣7x2+12＝0这是一个一元四次方程，根据该方程的特点，它的解法通常是：设x2＝y，则x4＝y2，∴原方程可化为：y2﹣7y+12＝0，解得y1＝3，y2＝4，当y＝3时，x2＝3，x＝±，当y＝4时，x2＝4，x＝±2．∴原方程有四个根是：x1＝，x2＝﹣，x3＝2，x4＝﹣2，以上方法叫换元法，达到了降次的目的，体现了数学的转化思想，运用上述方法解答下列问题．

（1）解方程：（x2+x）2﹣5（x2+x）+4＝0；

（2）已知实数a，b满足（a2+b2）2﹣3（a2+b2）﹣10＝0，试求a2+b2的值．

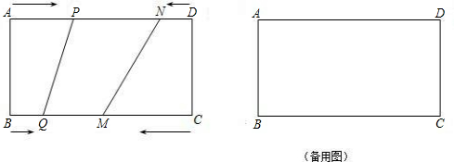
27．（9分）如图，在矩形ABCD中，BC＝20cm，P、Q、M、N分别从A、B、C、D出发，沿AD、BC、CB、DA方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止、已知在相同时间内，若BQ＝xcm（x≠0），则AP＝2xcm，CM＝3xcm，DN＝x2cm．

（1）当x为何值时，点P、N重合；

（2）当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形．

参考答案

一．选择题

1．D．2．A．4．C．5．D．6．B．7．C．8．A．9．C．10．D．

二．填空题

11．±4．    12．3，﹣4．    13．16．    14．121．    15．．    16．10．    17．．

三．解答题

18．解：（1）方程整理得：x2+2x＝，

配方得：x2+2x+1＝，即（x+1）2＝，

开方得：x+1＝±，

解得：x1＝﹣1+，x2＝﹣1﹣；

（2）分解因式得：（x﹣10）（x+2）＝0，

所以x﹣10＝0或x+2＝0，

解得：x1＝10，x2＝﹣2．

19．解：（1）根据题意得Δ＝22﹣4（m﹣1）≥0，

解得m≤2；

（2）根据题意得x1+x2＝﹣2，x1•x2＝m﹣1，

∵++3x1•x2+10＝0，

∴（x1+x2）2+x1•x2+10＝0，

∴（﹣2）2+m﹣1+10＝0，

∴m＝﹣13．

20．解：设应邀请x所学校参加比赛，

根据题意得：x（x﹣1）＝28，

整理得：x2﹣x﹣56＝0，

解得：x1＝8，x2＝﹣7（不符合题意，舍去）．

答：应邀请8所学校参加比赛．

21．解：由题意得1+x+x•x＝73，

即x2+x﹣72＝0，

∴（x+9）（x﹣8）＝0，

解得x1＝8，x2＝﹣9（舍去）

答：每个支干长出8个小分支．

22．解：设横向小道的宽为2x米，则竖向小道的宽为3x米，

由题意，得（30﹣3x）（20﹣2x）＝486．

解得x1＝1，x2＝9（舍去）．

则2x＝2．

答：横向小道的宽为2米．

23．解：（1）原式＝x2+6x+9﹣10＝（x+3）2﹣10．

∵（x+3）2≥0，

∴（x+3）2﹣10≥﹣10．

∴当x＝﹣3时，x2+6x﹣1的最小值是﹣10．

（2）∵a2﹣6b＝﹣14，b2﹣8c＝﹣23，c2﹣4a＝8，

∴a2﹣6b+b2﹣8c+c2﹣4a＝﹣29．

∴（a2﹣4a+4）+（b2﹣6b+9）+（c2﹣8c+16）﹣29＝﹣29．即（a﹣2）2+（b﹣3）2+（c﹣4）2＝0．

∵（a﹣2）2≥0，（b﹣3）2≥0，（c﹣4）2≥0．

∴（a﹣2）2＝0，（b﹣3）2＝0，（c﹣4）2＝0，

解得a＝2，b＝3，c＝4．

∴△ABC的周长为a+b+c＝9．

24．解：（1）设二、三这两个月的月平均增长率为x，

根据题意得：250（1+x）2＝360，

解得：x1＝0.2＝20%，x2＝﹣2.2（不符合题意，舍去）．

答：二、三这两个月的月平均增长率为20%；

（2）设商品降价y元，则每件商品的销售利润为（40﹣y﹣30）元，四月份的销售量为（360+6y）元，

根据题意得：（40﹣y﹣30）（360+6y）＝1950，

整理得：y2+50y﹣275＝0，

解得：y1＝5，y2＝﹣55（不符合题意，舍去）．

答：当商品降价5元时，商场获利4250元．

25．（1）证明：∵方程x2+px+q＝0是完美方程，

∴方程x2+px+q＝0中有两个相等的解，

∴Δ＝p2﹣4q＝0．

∴p2＝4q．

∵方程x2+px+q＝0是同族方程，

∴G＝＝4．

（2）解：设关于x的一元二次方程kx2﹣（k﹣3）x﹣3＝0的两根为x1，x2，

则x1+x2＝，x1•x2＝．

∵关于x的一元二次方程kx2﹣（k﹣3）x﹣3＝0属于同族方程，

∴，为整数．

∵k为整数，

∴k＝1或﹣1或3或﹣3．

26．解：（1）设y＝x2+x，则y2﹣5y+4＝0，

整理，得

（y﹣1）（y﹣4）＝0，

解得y1＝1，y2＝4，

当x2+x＝1即x2+x﹣1＝0时，解得：x＝；

当当x2+x＝4即x2+x﹣4＝0时，解得：x＝；

综上所述，原方程的解为x1，2＝，x3，4＝；

（2）设x＝a2+b2，则x2﹣3x﹣10＝0，

整理，得

（x﹣5）（x+2）＝0，

解得x1＝5，x2＝﹣2（舍去），

故a2+b2＝5．

27．解：（1）∵P，N重合，

∴2x+x2＝20，

∴，（舍去），

∴当时，P，N重合；

（2）因为当N点到达A点时，x＝2，此时M点和Q点还未相遇，

所以点Q只能在点M的左侧，

①当点P在点N的左侧时，依题意得

20﹣（x+3x）＝20﹣（2x+x2），

解得x1＝0（舍去），x2＝2，

当x＝2时四边形PQMN是平行四边形；

②当点P在点N的右侧时，依题意得

20﹣（x+3x）＝（2x+x2）﹣20，

解得x1＝﹣10（舍去），x2＝4，

当x＝4时四边形NQMP是平行四边形，

所以当x＝2或x＝4时，以P，Q，M，N为顶点的四边形是平行四边形．