2023-2024学年人教版七年级（上）第2章 整式的加减 单元检测卷

这是一份2023-2024学年人教版七年级（上）第2章 整式的加减 单元检测卷，共4页。
2023-2024学年人教版七年级（上）第2章 整式的加减 单元检测卷一．选择题（共10小题，满分30分，每小题3分）1．下列代数式中整式有（　　），2x+y，，，，0.5，aA．4个 B．5个 C．6个 D．7个2．下列各式中书写规范的是（　　）A．x6 B．3k÷2 C．m D．2n3．代数式﹣7x的意义可以是（　　）A．﹣7与x的和 B．﹣7与x的差 C．﹣7与x的积 D．﹣7与x的商4．下列整式中，是二次单项式的是（　　）A．x2+1 B．xy C．x2y D．﹣3x5．多项式a3b4﹣2a2b4+3的项数和次数分别是（　　）A．2，6 B．3，6 C．2，7 D．3，76．下列运算结果正确的是（　　）A．a+2a2＝3a2 B．3a2b﹣2ba2＝a2b C．5a﹣a＝5 D．2a+b＝2ab7．下面去括号错误的是（　　）A．a2﹣（a﹣b+c）＝a2﹣a+b﹣c B．5+a﹣2（3a﹣5）＝5+a﹣6a+5 C． D．a3﹣[a2﹣（﹣b）]＝a3﹣a2﹣b8．已知一个二位数的十位数字是5，个位数字是a，用代数式表示这个二位数是（　　）A．5a B．50a C．5+a D．50+a9．要使多项式mx2﹣（5﹣x+x2）化简后不含x的二次项，则m等于（　　）A．0 B．1 C．﹣1 D．﹣510．探索规律：观察下面的一列单项式：x​、﹣2x2、4x3、﹣8x4、16x5、…，根据其中的规律得出的第8个单项式是（　　）A．﹣64x8​ B．64x8​ C．128x8​ D．﹣128x8​二．填空题（共8小题，满分24分，每小题3分）11．﹣的系数是　                  　，次数是　   　．12．多项式3a2﹣2a﹣7a3+4是　   　次　   　项式．13．﹣3x2y﹣2x2y2+xy﹣4的最高次项为　         　．14．一根长80cm的弹簧，一端固定．如果另一端挂上物体，那么在正常情况下物体的质量每增加1kg可使弹簧增长2cm，正常情况下，当挂着xkg的物体时，弹簧的长度是　          　cm．（用含x的代数式表示）15．如果a＝，b＝﹣3，那么代数式2a+b的值为　     　．16．单项式3xmy2与﹣2x5yn是同类项，则m+n＝　   　．17．关于x的多项式x4+（a﹣1）x3+5x2﹣（b+3）x﹣1不含x3项和x项，求a+b＝　     　．18．4x与7的差不小于6用式子表示为 　         　．三．解答题（共7小题，满分46分）19．（6分）化简：（1）﹣2a+（3a﹣1）﹣（a﹣5）；    （2）﹣5+（x2+3x）﹣（﹣9+6x2）．    20．（6分）先化简，再求值：﹣6x+3（3x2﹣1）﹣（9x2﹣x+3），其中．    21．（6分）已知代数式A＝7x2﹣4x+3，B＝x2+3x﹣2．（1）求2A+B的值．（2）当x＝﹣2时，求（1）中式子的值．     22．（6分）某校七年级（1）（2）（3）（4）四个班的学生在植树节这天共植树（x+5）棵．其中（1）班植树x棵，（2）班植树的棵数比（1）班的2倍少40棵，（3）班植树的棵数比（2）班的一半多30棵．（1）求（1）（2）（3）班共植树多少棵？（用含x的式子表示）（2）若x＝40，求（4）班植树多少棵？     23．（6分）优优家买了一套房，地面结构如图所示：根据图中的数据（单位：米）解答下列问题：（1）用含m、n的式子表示地面的总面积；（2）若m2＝9，n的倒数等于本身，若铺1平方米地砖的费用为80元，那么优优家铺地砖所用的总费用是多少元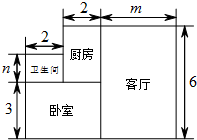？    24．（8分）已知M＝4x2﹣2x﹣1，N＝3x2﹣2x﹣5．（1）化简4M﹣（2M+3N），结果按照x的降幂排列；（2）当x＝﹣1时，求（1）中代数式的值；（3）试判断M、N的大小关系，并说明理由．      25．（8分）阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛，尝试应用整体思想解决下列问题：（1）把（a﹣b）2看成一个整体，合并2（a﹣b）2﹣6（a﹣b）2+5（a﹣b）2；（2）已知x2﹣2y＝﹣2，求6x2﹣12y﹣15的值；（3）已知a﹣2b＝﹣1，2b﹣c＝5，c﹣d＝﹣10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．