

2023年人教版九年级上册第22章《二次函数》章末检测卷
展开
这是一份2023年人教版九年级上册第22章《二次函数》章末检测卷,共5页。
2023年人教版九年级上册第22章《二次函数》章末检测卷满分120分 时间90分钟一、选择题(共30分)1.下列函数是二次函数的是( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.抛物线
2.抛物线![]() 的顶点的横坐标是( ).A.
的顶点的横坐标是( ).A.![]() B.
B.![]() C.
C.![]() D.03.在函数
D.03.在函数![]() ,y随x增大而减小,则x的取值范围为( )A.
,y随x增大而减小,则x的取值范围为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如果点
4.如果点![]() 在抛物线
在抛物线![]() 上,将此抛物线向右平移3个单位后,点
上,将此抛物线向右平移3个单位后,点![]() 同时平移到点
同时平移到点![]() ,那么
,那么![]() 坐标为( )A.
坐标为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.在同一坐标系中,一次函数
5.在同一坐标系中,一次函数![]() 与二次函数,
与二次函数,![]() 的图象可能是( )A.
的图象可能是( )A.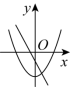 B.
B.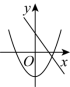 C.
C.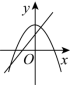 D.
D.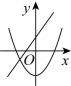 6.已知抛物线
6.已知抛物线![]() 与x轴只有一个交点,则m的值是( )A.2 B.
与x轴只有一个交点,则m的值是( )A.2 B.![]() C.1 D.
C.1 D.![]() 7.已知
7.已知![]() 都在函数
都在函数![]() 图象上,则
图象上,则![]() 的大小关系为( ).A.
的大小关系为( ).A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为
8.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为![]() 、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A.第8秒 B.第10秒 C.第12秒 D.第15秒9.如图,抛物线
、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )A.第8秒 B.第10秒 C.第12秒 D.第15秒9.如图,抛物线![]() 经过正方形
经过正方形![]() 的三个顶点A,B,C,点B在
的三个顶点A,B,C,点B在![]() 轴上,则
轴上,则![]() 的值为( )
的值为( )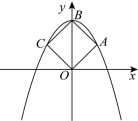 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,分别过点
10.如图,分别过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )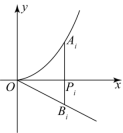 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(共32分)11.二次函数的概念:一般的,形如
二、填空题(共32分)11.二次函数的概念:一般的,形如![]() (
(![]() 是常数,
是常数,![]() )的函数叫做二次函数.其中 是自变量,
)的函数叫做二次函数.其中 是自变量,![]() 分别是函数解析式的 、 、常数项.12.二次函数
分别是函数解析式的 、 、常数项.12.二次函数![]() 的图象开口方向是 .13.抛物线
的图象开口方向是 .13.抛物线![]() 与
与![]() 轴的交点坐标是 .14.抛物线
轴的交点坐标是 .14.抛物线![]() 的对称轴是 .15.把抛物线
的对称轴是 .15.把抛物线![]() 向右平移1个单位,再向上平移2个单位,平移后的抛物线的解析式为 .16.长方形的周长为
向右平移1个单位,再向上平移2个单位,平移后的抛物线的解析式为 .16.长方形的周长为![]() ,其中一边长为
,其中一边长为![]() (其中
(其中![]() ),面积为
),面积为![]() ,则
,则![]() 与
与![]() 的关系式为 .17.如图,二次函数
的关系式为 .17.如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,则关于
,则关于![]() 的方程
的方程![]() 的根为 .
的根为 .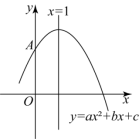 18.当
18.当![]() 时,二次函数
时,二次函数![]() 的最小值为 .三、解答题(共58分)19.(6分)已知二次函数
的最小值为 .三、解答题(共58分)19.(6分)已知二次函数![]() 的图像经过
的图像经过![]() ,
,![]() 两点.(1)求
两点.(1)求![]() 和
和![]() 的值;(2)试判断点
的值;(2)试判断点![]() 是否在此函数图像上? 20.(6分)在平面直角坐标系中
是否在此函数图像上? 20.(6分)在平面直角坐标系中![]() 中画出二次函数
中画出二次函数![]() 的图象.
的图象.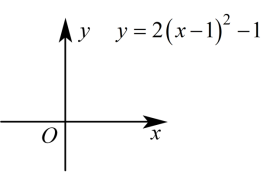 21.(8分)如图,已知二次函数
21.(8分)如图,已知二次函数![]() 的图象过
的图象过![]() 和
和![]() 两点,
两点,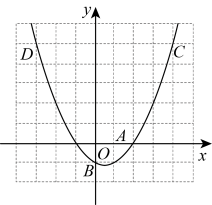 (1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线
(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线![]() ,并直接写出当x在什么范围内时,一次函数的值大于二次函数的值. 22.(8分)
,并直接写出当x在什么范围内时,一次函数的值大于二次函数的值. 22.(8分)![]() 年
年![]() 月
月![]() 日至
日至![]() 日,第
日,第![]() 届冬奥会在北京和张家口举办,这是中国历史上第一次举办冬奥会,吉祥物“冰墩墩”深受大家的喜爱.某超市在今年1月份销售“冰墩墩”
届冬奥会在北京和张家口举办,这是中国历史上第一次举办冬奥会,吉祥物“冰墩墩”深受大家的喜爱.某超市在今年1月份销售“冰墩墩”![]() 个,“冰墩墩”十分畅销,
个,“冰墩墩”十分畅销,![]() 、
、![]() 月份销售量持续走高,在售价不变的基础上,
月份销售量持续走高,在售价不变的基础上,![]() 月份的销售量达到
月份的销售量达到![]() 个.(1)求“冰墩墩”
个.(1)求“冰墩墩”![]() 、
、![]() 这两个月销售量的月平均增长率;(2)若“冰墩墩”每个进价
这两个月销售量的月平均增长率;(2)若“冰墩墩”每个进价![]() 元,原售价为每个
元,原售价为每个![]() 元,该超市在今年
元,该超市在今年![]() 月份进行降价促销,经调查发现,若“冰墩墩”在
月份进行降价促销,经调查发现,若“冰墩墩”在![]() 月份的基础上每个降价
月份的基础上每个降价![]() 元,销售量可增加
元,销售量可增加![]() 个,当“冰墩墩”每个售价为多少元时,出售“冰墩墩”在
个,当“冰墩墩”每个售价为多少元时,出售“冰墩墩”在![]() 月份利润最大,最大利润为多少元? 23.(9分)在平面直角坐标系中,已知抛物线
月份利润最大,最大利润为多少元? 23.(9分)在平面直角坐标系中,已知抛物线![]() 和直线
和直线![]() ,点
,点![]() 、
、![]() 均在直线
均在直线![]() 上.(1)求直线
上.(1)求直线![]() 的表达式;(2)若抛物线
的表达式;(2)若抛物线![]() 与直线
与直线![]() 有交点,求
有交点,求![]() 的取值范围;(3)当
的取值范围;(3)当![]() ,二次函数
,二次函数![]() 的自变量
的自变量![]() 满足
满足![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值. 24.(9分)某公司为城市广场上一雕塑
的值. 24.(9分)某公司为城市广场上一雕塑![]() 安装喷水装置.喷水口位于雕塑的顶端点B处,距离地面
安装喷水装置.喷水口位于雕塑的顶端点B处,距离地面![]() ,喷出的水柱轨迹呈抛物线型.据此建立如图的平面直角坐标系.若喷出的水柱轨迹
,喷出的水柱轨迹呈抛物线型.据此建立如图的平面直角坐标系.若喷出的水柱轨迹![]() 上,任意一点与支柱
上,任意一点与支柱![]() 的水平距离x(单位:
的水平距离x(单位:![]() )与广场地面的垂直高度为y(单位:
)与广场地面的垂直高度为y(单位:![]() )满足关系式
)满足关系式![]() ,且点
,且点![]() 在抛物线
在抛物线![]() 上
上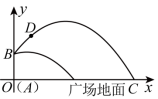 (1)求该抛物线的表达式;(2)求水柱落地点与雕塑
(1)求该抛物线的表达式;(2)求水柱落地点与雕塑![]() 的水平距离;(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:新喷水轨迹形成的抛物线形为
的水平距离;(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:新喷水轨迹形成的抛物线形为![]() ,把水柱喷水的半径(动态喷水时,点C到
,把水柱喷水的半径(动态喷水时,点C到![]() 的距离)控制在7
的距离)控制在7![]() 到14
到14![]() 之间,请探究改建后喷水池水柱的最大高度 25.(12分)如图,已知
之间,请探究改建后喷水池水柱的最大高度 25.(12分)如图,已知![]() .
.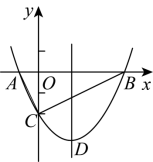 (1)求抛物线的解析式;(2)求三角形
(1)求抛物线的解析式;(2)求三角形![]() 的面积;(3)若点E在抛物线上,且三角形
的面积;(3)若点E在抛物线上,且三角形![]() 面积是三角形
面积是三角形![]() 面积的一半,求E点坐标.
面积的一半,求E点坐标.






