2022-2023学年甘肃省武威九中、爱华育新学校等三校九年级（下）期中数学试卷（含解析）

这是一份2022-2023学年甘肃省武威九中、爱华育新学校等三校九年级（下）期中数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年甘肃省武威九中、爱华育新学校等三校九年级（下）期中数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
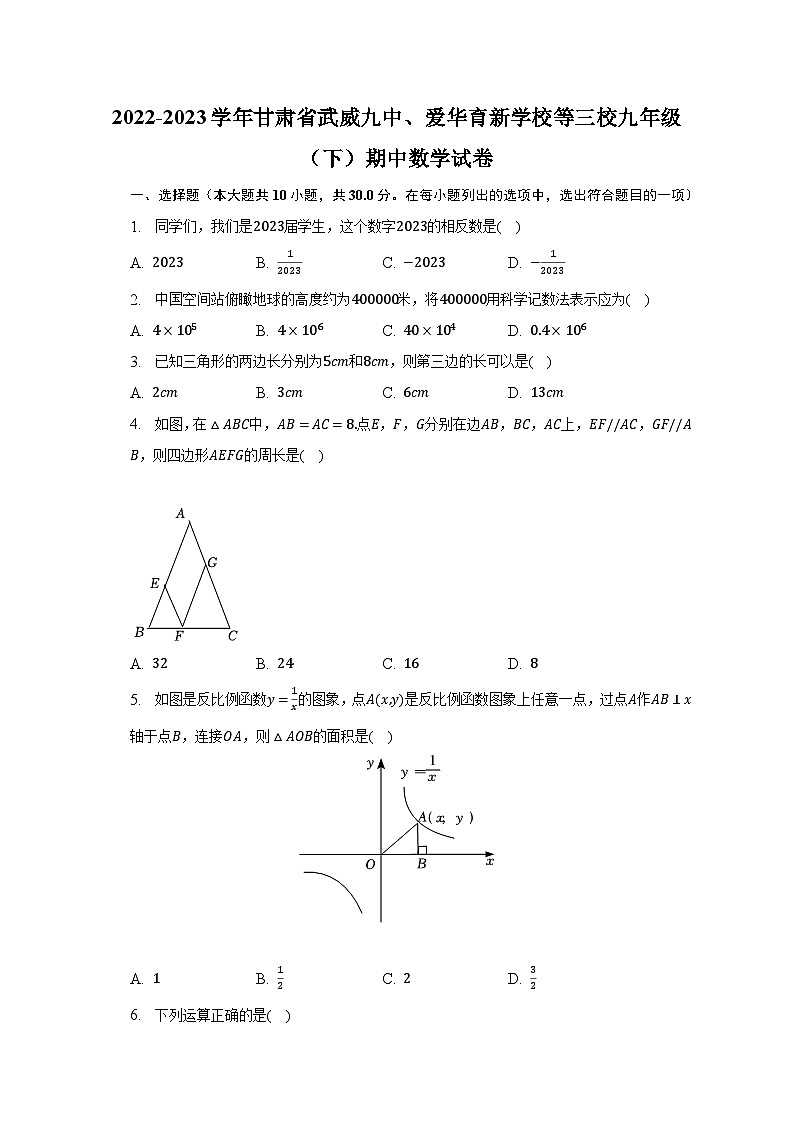
1. 同学们，我们是2023届学生，这个数字2023的相反数是(    )
A. 2023 B. 12023 C. −2023 D. −12023
2. 中国空间站俯瞰地球的高度约为400000米，将400000用科学记数法表示应为(    )
A. 4×105 B. 4×106 C. 40×104 D. 0.4×106
3. 已知三角形的两边长分别为5cm和8cm，则第三边的长可以是(    )
A. 2cm B. 3cm C. 6cm D. 13cm
4. 如图，在△ABC中，AB=AC=8.点E，F，G分别在边AB，BC，AC上，EF//AC，GF//AB，则四边形AEFG的周长是(    )


A. 32 B. 24 C. 16 D. 8
5. 如图是反比例函数y=1x的图象，点A(x,y)是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是(    )

A. 1 B. 12 C. 2 D. 32
6. 下列运算正确的是(    )
A. 2+ 3= 5 B. 30=0 C. (−2a)3=−8a3 D. a6÷a3=a2
7. 若一次函数y=2x+1的图象经过点(−3,y1)，(4,y2)，则y1与y2的大小关系是(    )
A. y1y2 C. y1≤y2 D. y1≥y2
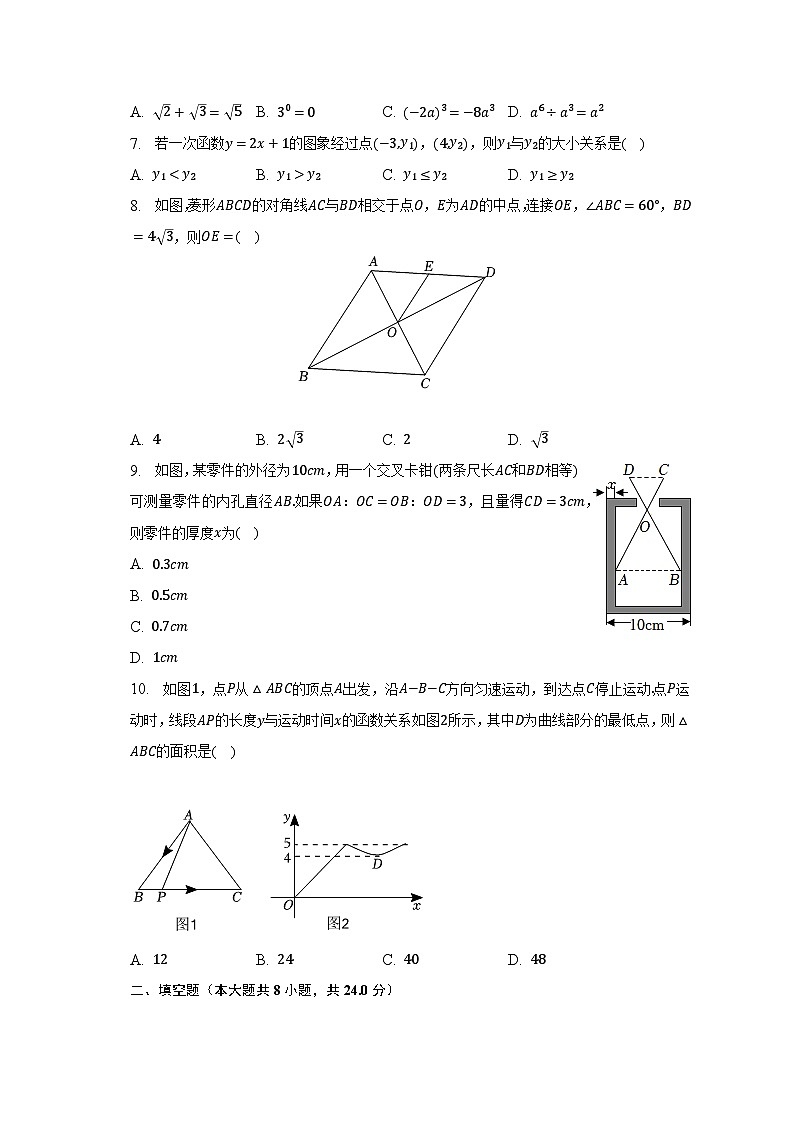
8. 如图，菱形ABCD的对角线AC与BD相交于点O，E为AD的中点，连接OE，∠ABC=60°，BD=4 3，则OE=(    )

A. 4 B. 2 3 C. 2 D. 3
9. 如图，某零件的外径为10cm，用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA：OC=OB：OD=3，且量得CD=3cm，则零件的厚度x为(    )
A. 0.3cm
B. 0.5cm
C. 0.7cm
D. 1cm
10. 如图1，点P从△ABC的顶点A出发，沿A−B−C方向匀速运动，到达点C停止运动.点P运动时，线段AP的长度y与运动时间x的函数关系如图2所示，其中D为曲线部分的最低点，则△ABC的面积是(    )


A. 12 B. 24 C. 40 D. 48
二、填空题（本大题共8小题，共24.0分）
11. 已知△ABC是等腰三角形．若∠A=40°，则△ABC的顶角度数是          ．
12. 请填写一个常数，使得关于x的方程x2−2x+          =0有两个不相等的实数根．
13. 已知x+y=4，x−y=6，则x2−y2=          ．
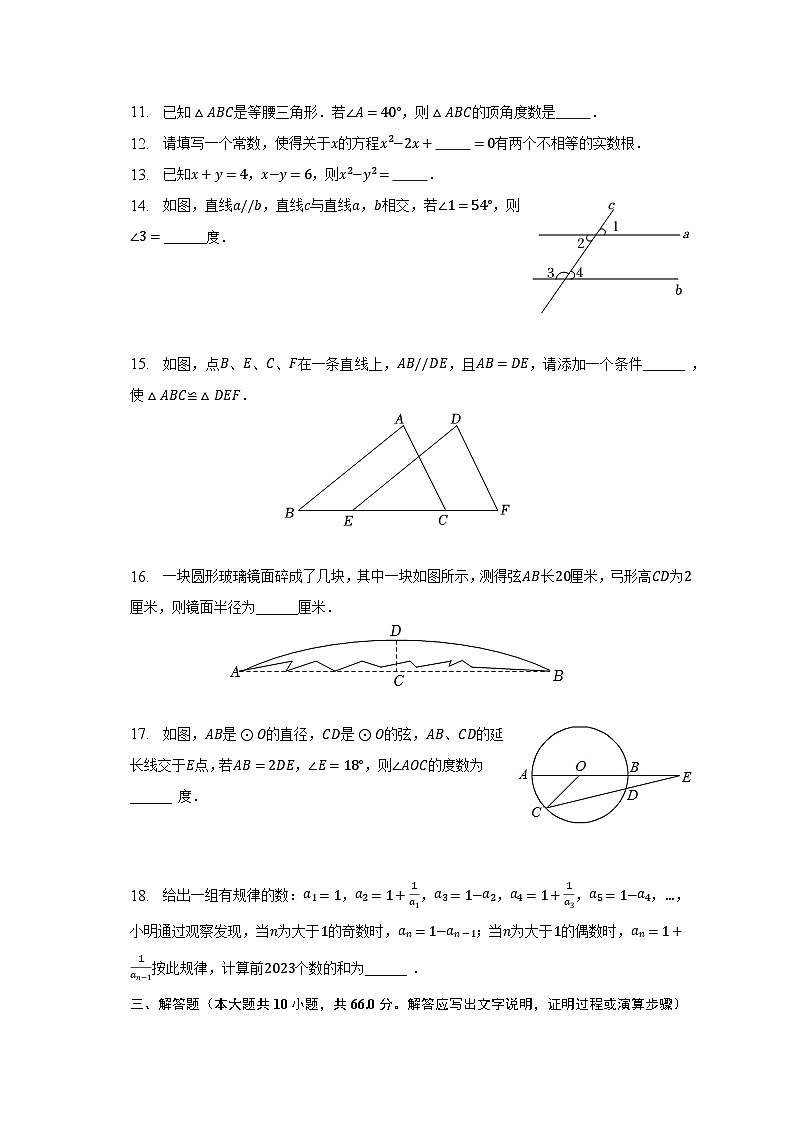
14. 如图，直线a//b，直线c与直线a，b相交，若∠1=54°，则∠3=______度．


15. 如图，点B、E、C、F在一条直线上，AB//DE，且AB=DE，请添加一个条件______ ，使△ABC≌△DEF．

16. 一块圆形玻璃镜面碎成了几块，其中一块如图所示，测得弦AB长20厘米，弓形高CD为2厘米，则镜面半径为______厘米．

17. 如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为______ 度．


18. 给出一组有规律的数：a1=1，a2=1+1a1，a3=1−a2，a4=1+1a3，a5=1−a4，…，小明通过观察发现，当n为大于1的奇数时，an=1−an−1；当n为大于1的偶数时，an=1+1an−1按此规律，计算前2023个数的和为______ ．
三、解答题（本大题共10小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题4.0分)
解不等式组x−3(x−2)≤102x−15>x−12，并把它的解集在数轴上表示出来．


20. (本小题4.0分)
先化简(a2−1a−3−a−1)÷a+1a2−6a+9，然后从−1，0，1，3中选一个合适的数作为a的值代入求值．
21. (本小题6.0分)
如图，在平行四边形ABCD中，AB>AD．
(1)尺规作图(保留作图痕迹，不写作法)：
①在AB上截取AE，使得AE=AD；
②作∠BCD的平分线交AB于点F．
(2)连接DE交CF于点P，猜想△CDP的形状，并证明你的结论．

22. (本小题6.0分)
如图，为了测量某矿山CH的高度，科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点，在A点观察H点的俯角为35°，然后乘坐直升机从A水平向前飞行500米到E点，此时观察H点的俯角为45°，所有的点都在同一平面内，科考队至此完成了数据监测，请你依据数据计算科考队测得的矿山高度(结果保留整数，参考数据：sn35°≈0.57，cos35°≈0.82，tan35°≈0.70， 2～1.41)

23. (本小题6.0分)
ETC(Electronic Toll Collection)不停车收费系统是目前世界上最先进的路桥收费方式.安装有ETC的车辆通过路桥收费站无需停车就能交纳费用.某高速路口收费站有A，B，C，D四个ETC通道，车辆可任意选择一个ETC通道通过，且通过每个ETC通道的可能性相同，一天，小李和小赵分别驾驶安装有ETC的汽车经过此收费站．
(1)求小李通过A通道的概率；
(2)请用列表或画树状图的方法表示出两人通过此收费站的所有可能结果，并求出小李和小赵经过相同通道的概率．
24. (本小题6.0分)
为了落实《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神，全面推动阳光体育运动在全国的深入实施.某区教育局在全区中学生对课外体育运动项目的喜欢程度进行调查，随机抽取了某校七年级部分学生进行问卷调查(每人限选一种体育运动项目)如图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

(1)求在这次调查中，一共调查了名学生？
(2)在扇形统计图中，“跳绳”所在的圆心角等于______ 度；
(3)喜欢“羽毛球”的人数是______ ；
(4)请补全条形统计图；
(5)若该校有七年级学生1500人，请你估计该校七年级喜欢“足球”的学生有多少人？
25. (本小题6.0分)
如图，直线y=mx+n与双曲线y=kx相交于A(−1,3)、B(3,b)两点，与y轴相交于点C．
(1)求直线AB的解析式；
(2)若点D与点C关于x轴对称，求△ABD的面积；
(3)不用计算，请直接写出不等式mx+n≥kx的解集．

26. (本小题8.0分)
如图，AB是⊙O的直径，点F在⊙O上，∠BAF的平分线AE交⊙O于点E，过点E作ED⊥AF，交AF的延长线于点D，延长DE，AB相交于点C．
(1)求证：CD是⊙O的切线；
(2)若⊙O的半径为5，tan∠EAD=12，求DE的长．

27. (本小题8.0分)
【问题情境】：数学活动课上，老师出示了一个问题：如图1，在正方形ABCD中，E是BC的中点，AE⊥EP，EP与正方形的外角∠DCG的平分线交于P点，试猜想AE与EP的数量关系，并加以证明．
(1)【思考尝试】：有同学发现，取AB的中点F，连接EF可以解决这个问题.请在图1中补全图形，解答老师提出的问题；
(2)【实践探究】：有同学受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形ABCD中，E为BC边上一动点(点E与B不重合)，当△AEP是等腰直角三角形，∠AEP=90°，连接CP，可以求出∠DCP的大小，请你思考并解答这个问题．
28. (本小题12.0分)
如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上，抛物线y=−x2+bx+c经过A，C两点，与x轴交于另一个点D．

(1)①求b，c的值；
②在平面内是否存在点Q，使得以点A、C、D、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由；
(2)若点P是边BC上的一个动点，连接AP，过点P作PM⊥AP，交y轴于点M(如图2所示)，当点P在BC上运动时，点M也随之运动，设BP=m，CM=n，试用含m的代数式表示n，并求出n的最大值．
答案和解析

1.【答案】C 
【解析】解：2023的相反数为−2023，
故选：C．
根据相反数的定义(只有符号不同的两个数)判断即可．
本题考查了相反数的定义，熟悉相反数的定义是解题关键．

2.【答案】A 
【解析】解：400000=4×105．
故选：A．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|