












人教版数学九年级下册 26.3.2第12讲《反比例函数》专项复习 课件+教案+分层练习+预习案
展开人教版数学九年级下册
26.3.2第12讲《反比例函数》专项复习分层练习
【基础篇】
测试题1 如果反比例函数![]() 的图象经过点(-3,-4),那么函数的图应在( )
的图象经过点(-3,-4),那么函数的图应在( )
A. 第一、三象限 B. 第一、二象限
C. 第二、四象限 D. 第三、四象限
答案:A
解析过程:因为(-3,-4)在第三限,所以k<0,反比例函数的图应在第一、三限.故选:A.
测试题2 在函数![]() 的图象上有三点(-1,y1),
的图象上有三点(-1,y1),![]() ,
,![]() 则函数值y1、y2、y3的大小关系是( )
则函数值y1、y2、y3的大小关系是( )
A. y2<y3<y1 B.y3<y2<y1
C.y1<y2<y3 D.y3<y1<y2
答案:C
解析过程:![]()
![]()
故选C.
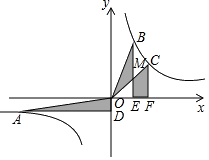
测试题3 如图所示,在直角平面坐标系Oxy中,点A、B、C为反比例函数![]() (k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
(k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则( )
A. S1=S2+S3 B. S2=S3
C. S3>S2>S1 D. S1S2<S32
答案:B
解析过程:
∵点A、B、C为反比例函数y=![]() (k>0)上不同的三点,AD⊥y轴,BE,CF垂直x轴于点E、F,
(k>0)上不同的三点,AD⊥y轴,BE,CF垂直x轴于点E、F,
∴S1=![]() k,S△BOE=S△COF=
k,S△BOE=S△COF=![]() k,
k,
∵S△BOE﹣S△OME=S△CDF﹣S△OME,
∴S3=S2,
故选B.
测试题4 设有反比例函数![]() ,(x1,y1)、(x2,y2)为其图象上的两点,若x1<0<x2时y1>y2,则k的取值范围是( )
,(x1,y1)、(x2,y2)为其图象上的两点,若x1<0<x2时y1>y2,则k的取值范围是( )
A. k>0 B. k<0 C. k>-1 D. k<-1
答案:D
【能力篇】
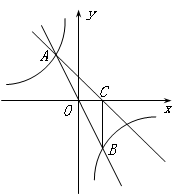
测试题5 如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
解析过程:
(1)∵直线![]() 与双曲线
与双曲线![]() 相交于A(-1,a)、B两点,
相交于A(-1,a)、B两点,
∴B点横坐标为1,即C(1,0)
∵△AOC的面积为1,
∴A(-1,1)
将A(-1,1)代入![]() ,
,![]() 可得m=-1,n=-1;
可得m=-1,n=-1;
(2)设直线AC的解析式为y=kx+b
∵y=kx+b经过点A(-1,1)、C(1,0)
∴![]() 解得k=-
解得k=-![]() ,b=
,b=![]() .
.
∴直线AC的解析式为y=-![]() x+
x+![]() .
.
【拔高篇】
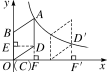
6.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(x>0)的图象上,点D的坐标为(4,3).
(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数y=(x>0)的图象上时,求菱形平移的距离.

14.解:(1)如图,过点D作DE⊥y轴于点E,DF⊥x轴于点F,
∵点D的坐标为(4,3),∴FO=4,DF=3,∴DO=5.
∵四边形ABCD为菱形,∴AD=DO=5,∴A点坐标为(4,8).
又∵点A(4,8)在反比例函数y=(x>0)的图象上,∴k=4×8=32;
(2)将菱形ABCD向右平移,使点D落在反比例函数y=(x>0)的图象上的D′点,
过点D′作D′F′⊥x轴于F′.
∵DF=3,∴D′F′=3,∴D′点的纵坐标为3,
∴OF′=,∴FF′=OF′-OF=-4=,
∴菱形ABCD向右平移的距离为.










