

数学选择性必修 第一册1.1 空间向量及其运算第1课时教学设计
展开1.1.1空间向量及其线性运算(第一课时)
(人教A版2019普通高中教科书数学选择性必修第一册第一章)
一、教学目标
(1)理解空间向量的概念,掌握空间向量的表示方法;会用图形说明空间向量加法,减法,数乘向量及它们的运算律;
(2)会用向量共线和向量共面充要条件;
(3)会用空间向量的运算及运算律解决简单的立体几何问题;形成事物与事物之间普遍联系及其相互转化的辨证观点;
(4)通过探究、练习,提高学生对事物个性与共性之间联系的认识水平,提升学生的直观想象、数学运算、逻辑推理等数学学科核心素养.
二、教学重难点
教学重点:空间向量的概念和线性运算及其应用
教学难点:空间向量的线性运算及其应用
三、教学过程
(一)创设情境,导入新课
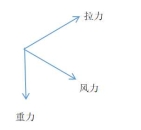
师生活动:阅读章前引言,章头图展示的是一个做滑翔伞运动的场景,可以想象在滑翔过程中,飞行员会受到来自不同方向大小各异的力,你能用图示法表示这些力吗?
设计意图:图1中的引入情境于学生而言,非常熟悉。课堂上追问学生,飞行员收到来自不同方向的力又该如何表示,用图示法表示这些力吗?既贴近学生生活实际又自然将平面向量拓展到空间向量,既揭示了学习空间向量的必要性,又激发了学生的学习兴趣,也为后续空间向量的加法运算做了铺垫(尤其是在验证空间向量的加法结合律).

(二)类比归纳,形成概念
问题1 我们已经学习过平面向量的概念和线性运算,你能类比平面向量,给出空间向量的概念和线性运算吗?
追问(1):平面向量是什么的?你能类比平面向量给出空间向量的概念吗?
追问(2):如何表示平面向量??你能类比平面向量的表示,给出空间向量的表示吗?
追问(3):从平面向量的概念出发,我们又学习了不少新的概念. 你还记得吗?有哪些?你能把这些概念推广到空间向量中吗?
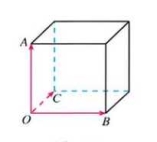
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量,空间向量的大小叫做空间向量的长度或模.与平面向量一样,空间向量也用有向线段来表示,有向线段的长度表示空间向量的模。空间向量可以用字母a,b,c,…表示.如图,若向量a的起点是A,终点是B,则向量a也可以记作向量AB,其模记为向量a的模或向量AB的模.如图所示,对于任意一个空间向量,我们都可以将其放在一个平面内研究,这时,这个空间向量就是我们熟悉的平面向量了.
| 空间向量 |
定义 | 既有大小又有方向的量 |
平移 | 自由向量,平移后不发生改变 |
表示法 | 几何表示: 字母表示: |
向量的模 | 向量的大小: |
相等向量 | 方向相同且长度相等 |
相反向量 | 方向相反且长度相等 |
单位向量 | 长度为1的向量 |
零向量 | 长度为0的向量 |
共线向量 (平行向量) | 方向相同或相反的非零向量 |
问题2 在学习完平面向量的相关概念以后,我们研究了平面向量的线性运算.你能类比平面向量的线性运算,得出空间向量的线性运算及运算律吗?
追问(1):平面向量的线性运算有哪些?我们如何研究这些运算?
答:平面向量有加法、减法和数乘运算. 先研究它们的定义及运算法则,再研究它们的运算律;
追问(2):平面向量的加法、减法和数乘运算的定义或法则分别是什么?你能类比它们得出空间向量的加、减和数乘运算的定义或法则吗?
追问(3):平面向量线性运算的运算律有哪些?你能类比它们得出空间线性运算的运算律吗?
由于任意两个空间向量都可以通过平移,转化为同一平面内的向量,因此,我们猜想,空间向量的线性运算也具有和平面向量线性运算相同的运算律.
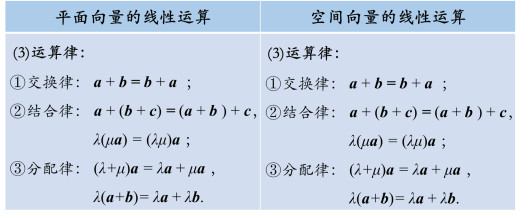
数学结论是需要严格证明的, 由合情推理、猜想得到的结论不一定正确,需要严格证明.
追问(4):空间向量线性运算运算律的证明,和平面向量有哪些异同?
除空间向量加法的结合律以外,其他运算律都可以转化为平面向量线性运算的运算律进行证明.结合律涉及三个向量,它们可能不在同一个平面内.
追问(5)如何证明空间向量的加法结合律呢?
如图,可将空间中任意三个不共面的向量,通过平移使它们起点重合,分别平移表示表示这三个向量的线段,构成一个平行六面体. 我们借助这个平行六面体来证明加法的结合律.
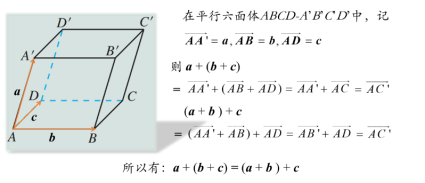
一般地,对于三个不共面的向量a,b, c,以任意点O为起点, a,b, c为邻边作平行六面体,则a,b, c的和等于以O为起点的平行六面体对角线所表示的向量.
问题3 平面向量的线性运算可以解决平面中的很多问题,空间向量的线性运算是否可以解决空间中相应的问题呢?
由平面向量的线性运算,我们研究了平面向量的共线及线性表示等问题.
追问(1):你还记得两个向量共线的充要条件吗?这个充要条件对于空间向量也成立吗?
追问(2):任意两个空间向量都可以通过平移,移到同一平面内,三个向量呢?
答:任意两个空间向量总是共面的,但三个空间向量既可能共面,也可能不共面.
追问(3):你还记得平面向量基本定理的内容吗?它和三个空间向量共面有什么关系?
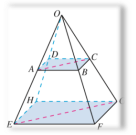 问题4 如右图,已知平行四边形ABCD,过平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
问题4 如右图,已知平行四边形ABCD,过平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使![]() .
.
求证: E,F,G,H 四点共面.
追问(1):如何证明E,F,G,H 四点共面?
答:可以通过证明E,F,G,H这四点构成的三个向量,如
![]() 共面,来证明这四点共面.
共面,来证明这四点共面.
追问(2):如何证明这三个向量共面?
答:根据向量共面的充要条件,用![]() 表示
表示![]() 即可.
即可.
追问(3):如何实现上述表示?
答:可以根据三角形法则,把![]() 分别用
分别用![]() 等向量来表示;再利用已知条件,将它们转化用
等向量来表示;再利用已知条件,将它们转化用![]() 表示的形式.而由已知平行四边形ABCD,得到
表示的形式.而由已知平行四边形ABCD,得到![]() ,从而可以得到
,从而可以得到![]() 的关系,进一步得到
的关系,进一步得到![]() 的关系,最终用用
的关系,最终用用![]() 表示
表示![]() .
.
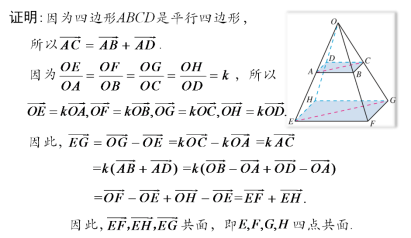
思路小结:选择恰当的向量表示问题中的几何元素,通过向量运算得出几何元素的关系是解决立体几何问题的常用方法.
问题5 回顾本节课的探究过程,你都学到了什么?
2. 从本节课的研究方法上来看,我们始终类比平面向量的相关内容,在空间中进行推广,同时比较它与平面向量的共性和差异,并对差异之处进行了严格的证明,最终,在平面向量的相关内容推广过程中,既保持了原结论的延续性,又保证了新结论的严谨性.原有内容的融入到新内容中,这种兼容性是数学的特点, 是数学中常用的研究方法.今后继续研究空间向量的过程中,还会不断使用这样的方法.希望同学们在今后的学习中,继续大胆发现,勇于探索,严谨推理,体会数学的逻辑之美,严谨之美和广泛的应用.
四、课外作业
布置作业:教科书练P9复习巩固1,2,3,4
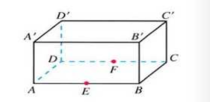
1.如图,E,F分别是长方体![]() 的棱
的棱![]() 的中点,化简下列表达式,并在图中标出化简结果的向量:
的中点,化简下列表达式,并在图中标出化简结果的向量:
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
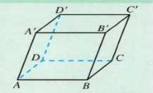
2.如图,用![]() 表示
表示![]() .
.
3.如图,已知正方体![]() ,
,![]() 分别是上底面
分别是上底面![]() 和侧面
和侧面![]() 的中心,求下列各式中x,y的值:
的中心,求下列各式中x,y的值:
(1)![]()
(2)![]()

设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、数学建模的核心素养.
【小单元教案】高中数学人教A版(2019)选修第一册--1.1.1 空间向量及其线性运算(课时教学设计): 这是一份【小单元教案】高中数学人教A版(2019)选修第一册--1.1.1 空间向量及其线性运算(课时教学设计),共8页。
人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算第1课时教案: 这是一份人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算第1课时教案,共4页。教案主要包含了教学目标,教学重难点等内容,欢迎下载使用。
数学选择性必修 第一册1.1 空间向量及其运算第2课时教案设计: 这是一份数学选择性必修 第一册1.1 空间向量及其运算第2课时教案设计,共5页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。













