人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算第1课时教案

这是一份人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算第1课时教案，共4页。教案主要包含了教学目标，教学重难点等内容，欢迎下载使用。
1.1.2空间向量的数量积运算（第一课时）(人教A版普通高中教科书数学选择性必修第一册第一章)一、教学目标1.了解空间向量夹角的概念及表示方法，掌握空间向量数量积的计算方法、几何意义、性质及运算律2.通过学习空间向量的数量积运算，培养学生数学运算的核心素养；通过投影向量概念的学习培养学生直观想象和逻辑推理的核心素养二、教学重难点1.重点：空间向量的数量积的定义、性质、运算律及计算方法2.难点：空间向量的数量积的几何意义，运算律的证明三、教学过程1.类比平面向量，探究空间向量数量积的相关概念和性质1.1两个非零空间向量的夹角问题1：类比平面向量中所学，如何定义空间向量的夹角？【预设的答案】空间向量是自由向量，可以将两个向量平移到共起点的位置（动态演示空间向量平移过程）【定义】已知两个非零向量a，b，在空间任取一点O，作 = a， = b，则∠AOB叫做向量a，b的夹角，记作〈a，b〉. 规定：〈a，b〉∈[0，π].特别地：当〈a，b〉= 时，a⊥b.【互动练习】（1）〈a，b〉=〈b，a〉成立吗？     [（2）〈a，b〉=       ，则称a与b互相垂直，记作      .（3）〈a，b〉= 0时,a与b方向       ; 〈a，b〉= π时,a与b方向       .来1.2 两个非零空间向量的数量积【定义】已知两个非零向量a，b，则|a| |b| cos〈a，b〉叫做a，b的数量积，记作a·b. 即a·b = |a| |b| cos〈a，b〉.规定：零向量与任意向量的数量积都等于零.问题2：根据上述定义我们不难发现，空间向量数量积的定义和平面向量数量积定义一致，那么空间向量数量积的性质是否与平面向量中的一致呢？【预设的答案】一致【互动练习】（1）两个向量的数量积是数量还是向量？（数量，它的大小与两个向量的长度及其夹角有关.）（2）0 ·a =       （选择0还是0）. 零向量与任意向量的数量积为0.（3）对于两个非零向量a，b，a⊥b ⟺ a·b =     （判断垂直关系）（4）a·a＝_____或|a|＝（求模长）（5）若a，b同向，则 a·b＝_______；若反向，则a·b＝_______.（6）|a·b| ____ |a|·|b|（7）若θ为a，b的夹角，则cos θ＝_______.【设计意图】平面向量中关于数量积的性质可以直接类比到空间向量中来，从学生的口中叙述出来，一是为了巩固，也能让学生体会空间向量数量积定义与平面向量数量积定义的相通之处.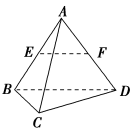【例1】如图所示，在棱长为1的正四面体ABCD中，E，F分别是AB，AD的中点，求值： (1)·；(2)·；(3)·.【解】(1)·＝·＝||||cos〈，〉＝cos 60°＝.(2)·＝·＝||2＝.(3)EF·＝·＝－·＝－×cos 60°＝－.1.3 空间向量的数量积的几何意义问题3:在平面向量的学习中，我们学习了向量的投影.类似地，在空间，向量a向向量b的投影有什么意义？【预设的答案】将两空间向量平移至同一平面，转化为平面向量问题，找出投影向量.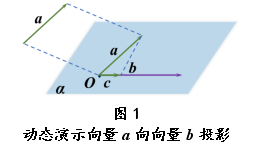在空间中，由于向量a与向量b是自由向量，将向量a与向量b平移到同一平面内?内，进而利用平面上向量的投影，得到与向量b共线的向量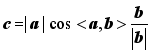： 追问: 空间中，向量a能否向一条直线l作投影？向量a能否向一个平面β作投影？ 注：图3中向量a与投影向量的夹角就是向量a所在直线与平面β所成的角【设计意图】投影向量概念的提出是为了让学生体会空间向量数量积的几何意义；另外，空间向量向直线投影、向平面投影也为后续学生对空间向量与空间角间的关系形成初步认识.1.4 空间向量的数量积的运算律问题4: 类比平面向量数量积的运算律，空间向量数量积满足哪些运算律？ 【预设的答案】结合律；交换律；分配律数乘向量与向量数量积的结合律(λa)·b＝λ(a·b), λ∈R交换律a·b＝b·a分配律a·(b＋c)＝a·b＋a·c追问：你能否证明上述运算律？【教师分析】证明前两条运算律，可以将向量a与向量b平移至同一个平面当中，则证明过程与平面向量中的证明方法无异；证明分配律时则涉及到三个不共面的向量.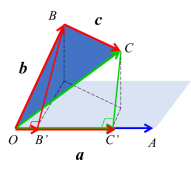分配律的证明：,,,, 对比思考，深入了解思考问题1: 对于三个均不为0的数a，b，c，若ab=ac，则b=c.对于非零向量a，b，c，由a·b＝a·c，能得到b＝c吗？分析：由a·b＝a·c，有a·(b－c)＝0. 从而有b＝c或a⊥(b－c).追问：能否从几何意义的角度举出反例？思考问题2: 向量有除法吗？分析：向量没有除法.追问：的结果唯一吗？思考问题3: 向量数量积满足结合律吗？分析：两个向量的数量积为一个实数，(a·b)c和a(b·c)分别表示与向量c和向量a共线的向量，它们不一定相等.向量的数量积运算没有结合律！【设计意图】通过三个问题的思考 ，与数字运算进行对比，深刻体会向量运算与数字运算的区别所在；学会用数形结合的思想解决问题，了解向量是与几何密切相关的工具.四、课堂小结（1）空间向量夹角的定义及范围；（2）空间向量数量积运算的定义、性质及几何意义；（3）空间向量数量积运算的运算律及简单计算.五、课后思考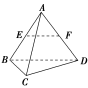【变式训练1】例1条件不变,如何求·的值?【解】·＝·(－)＝·－·＝||||cos〈，〉－||||cos〈，〉＝cos 60°－cos 60°＝0.【设计意图】感受向量数量积的逆用，数量积运算的结果可以推导出夹角及位置关系.思考：（1）能否利用空间向量的数量积证明空间中两条直线垂直？（2）能否利用空间向量的数量积求出空间中异面直线所成角？（3）能否利用空间向量的数量积解决更多的立体几何中的问题？