

高中人教A版 (2019)1.4 空间向量的应用第2课时教学设计及反思
展开1.4.2用空间向量研究距离、夹角问题(第二课时)
(人教A版普通高中教科书数学选择性必修第一册第一章)
一、教学内容
两条直线所成的角,直线与平面所成角,两个平面的夹角.
二、教学目标
1、理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成角.
2、理解直线与平面所成角与直线的方向向量和平面的法向量夹角之间的关系,会用向量方法求直线与平面所成角.
3、理解二面角大小与两个平面法向量夹角之间关系,会用向量方法求二面角的大小.
4、让学生体验向量方法在解决立体几何问题中的作用.
5、通过本节学习,提升学生的直观想象、数学运算、逻辑推理和数学抽象等数学学科核心素养.
三、教学重点与难点
重点:利用向量的数量积研究两条直线所成的角、直线与平面所成角、两个平面的夹角.
难点:根据问题的条件选择适当的基底.
四、教学过程设计
导入问题:与距离一样,角度是立体几何中的另一类度量问题.本质上,角度是对两个方向的差的度量,向量是有方向的量,所以利用向量研究角度问题有其独特的优势.本节我们用空间向量研究夹角问题,你认为可以按怎样的顺序展开研究.
 师生活动:学生独立思考、小组讨论后,通过全班讨论达成对研究路径的共识,即:直线与直线所成的角
师生活动:学生独立思考、小组讨论后,通过全班讨论达成对研究路径的共识,即:直线与直线所成的角![]() 直线与平面所成的角
直线与平面所成的角![]() 平面与平面所成的角.
平面与平面所成的角.
设计意图:明确研究路径,为具体研究提供思路.
1.典型例题,求解直线与直线所成的角
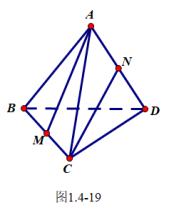
例7 如图1.4-19,在棱长为1的正四面体(四个面都是正三角形)![]() 中,
中,![]() 分别为
分别为![]() 的中点,求直线
的中点,求直线![]() 和
和![]() 夹角的余弦值.
夹角的余弦值.
用向量方法求解几何问题时,首先要用向量表示问题中的几何元素.对于本问题,如何用向量表示异面直线![]() 和
和![]() ?它们所成的角可以用向量之间的夹角表示吗?
?它们所成的角可以用向量之间的夹角表示吗?
追问1:这个问题的已知条件是什么?根据以往的经验,你打算通过什么途径将这个立体几何问题转化成向量问题?
师生活动:首先教师分析题目的条件:已知正四面体的棱长和棱与棱之间夹角,![]() 和
和![]() 是中线,其模长可求,与其他棱的夹角也是确定的,这些条件都有利用向量基底的选取.接着在学生回答的基础上,教师补充后形成共识:求异面直线
是中线,其模长可求,与其他棱的夹角也是确定的,这些条件都有利用向量基底的选取.接着在学生回答的基础上,教师补充后形成共识:求异面直线![]() 和
和![]() 的夹角时,只要用基底向量表示它们的方向即可,这样,异面直线
的夹角时,只要用基底向量表示它们的方向即可,这样,异面直线![]() 和
和![]() 的夹角,可以转化为求向量
的夹角,可以转化为求向量![]() 与向量
与向量![]() 的夹角.为此,选择
的夹角.为此,选择![]() 为基底并表示向量
为基底并表示向量![]() ,
,![]() .
.
在此基础上,将此问题推广到一般,学生思考后作答,教师对学生的回答给予补充.梳理出将立体几何问题转化成向量问题的途径:
途径1:通过建立一个基底,用空间向量表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题;
途径2:通过建立空间直角坐标系,用坐标表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题.实际上,空间直角坐标系也是基底,是“特殊”的基底.
追问2:请你通过向量运算,求出向量![]() ,
,![]() 夹角的余弦值,进而求出直线
夹角的余弦值,进而求出直线![]() 和
和![]() 夹角的余弦值.
夹角的余弦值.
师生活动:学生利用向量的数量的数量积求出向量![]() ,
,![]() 夹角的余弦值,从来解决问题.
夹角的余弦值,从来解决问题.
解:化为向量问题
以![]() 为基底,则
为基底,则![]() ,
,![]()
设向量![]() 夹角为
夹角为![]() ,则直线
,则直线![]() 和
和![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
进行向量运算
![]()
![]()
![]()
![]()
![]() ,
,
而![]() 都是正三角形,所以
都是正三角形,所以![]() ,
,
所以,  ,
,
回到图形问题
所以,直线![]() 和
和![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
小结:研究立体几何问题要注意转化思想,将立体几何问题化为向量问题![]() 进行向量运算
进行向量运算![]() 回到图形,解决立体几何问题.
回到图形,解决立体几何问题.
追问3:回顾问题1的求解过程,你能归纳出利用向量求空间直线与直线所成的角的一般方法吗?
师生活动:教师引导学生梳理,得出:将直线与直线所成的角转化成直线的方向向量的夹角,进而利用向量的数量积求解.也就是说,若异面直线![]() 所成的角为
所成的角为![]() ,其方向向量分别为
,其方向向量分别为![]() ,则
,则
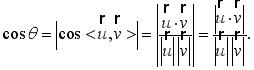
在此基础上,教师板书下面的过程,让学生进一步认识用向量方法解决几何问题的基本步骤:
几何问题![]() 向量问题
向量问题![]() 向量运算
向量运算![]() 几何解释
几何解释
设计意图:通过用向量方法求解一个空间直线与直线所成角的具体问题,归纳得出用向量方法求解直线与直线所成角的角度的一般方法.
2.类比研究,求解直线与平面、平面与平面所成的角
问题2:你能用向量方法求问题1中的直线![]() 与平面
与平面![]() 所成的角吗?一般地,如何求直线和平面所成的角?
所成的角吗?一般地,如何求直线和平面所成的角?
追问:这个问题的已知条件是什么?如何将几何问题转化成向量问题?
师生活动:教师引导学生分析已知条件,明确平面的法向量在解决直线与平面所成角的问题中的关键作用,将直线![]() 与平面
与平面![]() 所成的角转化成直线
所成的角转化成直线![]() 的一个方向向量与平面
的一个方向向量与平面![]() 的一个法向量的夹角,进而利用向量的数量积求解.
的一个法向量的夹角,进而利用向量的数量积求解.
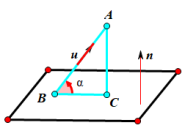 进一步地,师生共同给出求直线与平面所成角的步骤和方法.即将直线与平面所成的角转化为直线的方向向量与平面的法向量的夹角,从而得到直线与平面所成角的一般表达式
进一步地,师生共同给出求直线与平面所成角的步骤和方法.即将直线与平面所成的角转化为直线的方向向量与平面的法向量的夹角,从而得到直线与平面所成角的一般表达式
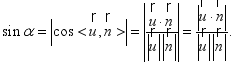
其中,![]() 为直线的方向向量,
为直线的方向向量,![]() 为平面的法向量.
为平面的法向量.
设计意图:通过本问题的解决,让学生体会法向量在求解直线与平面所成角时的关键作用,并得出一般的求解直线和平面所成角的量表达式.
问题3:类比已有的直线、平面所成角的定义,你认为应如何合理定义两个平面所成的角?进一步地,如何求平面和平面的夹角?
师生活动:教师给出两个相交平面的图形,让学生类比已有的空间基本元素所成角的定义,给两个平面所成的角下定义.教师可以追问学生:“角度是度量方向差异的量,那么决定平面方向的是什么?”从而启发学生用两个平面的法向量刻画两个平面所成的角.在学生讨论、交流的基础上,教师小结如下:
如右图,平面![]() 和平面
和平面![]() 相交,形成四个二面角,我们把这四个二面角中不大于
相交,形成四个二面角,我们把这四个二面角中不大于![]() 的二面角称为平面
的二面角称为平面![]() 和平面
和平面![]() 的夹角.
的夹角.
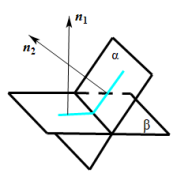 类似两条异面直线所成的角,若平面
类似两条异面直线所成的角,若平面![]() ,
,![]() 的法向量分别是
的法向量分别是![]() ,
,![]() ,则平面
,则平面![]() 和平面
和平面![]() 的夹角即为向量
的夹角即为向量![]() 和
和![]() 的夹角或其补角.
的夹角或其补角.
设平面![]() 和平面
和平面![]() 的夹角为
的夹角为![]() ,则
,则
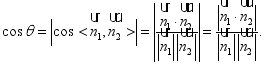
追问1:如何求平面的法向量?
师生活动:学生思考、回答后,师生共同总结求平面法向量的方法:在平面内找两个不共线的向量![]() 和
和![]() ,设平面的法向量为
,设平面的法向量为![]() ,则
,则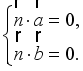
根据这个不定方程组,可以求得一个法向量![]() .
.
教师在学生回答的基础上进一步指出,求得的![]() 是法向量中的一个,不是所有的法向量,但所有法向量
是法向量中的一个,不是所有的法向量,但所有法向量![]() 可以用
可以用![]() 表示,即
表示,即![]() .
.
追问2:你能说说平面与平面的夹角与二面角的区别和联系吗?
师生活动:学生思考、回答,教师与学生共同总结.二面角的大小是指其两个半平面的张开程度,可以用其平面角![]() 的大小来定义,它的取值范围是
的大小来定义,它的取值范围是![]() ;而平面
;而平面![]() 和平面
和平面![]() 的夹角是指平面
的夹角是指平面![]() 和平面
和平面![]() 相交,形成的四个二面角中不大于
相交,形成的四个二面角中不大于![]() 的二面角.
的二面角.
设计意图:引导学生类比已有的空间基本元素所成角的定义,建立平面与平面的夹角的概念,并进一步利用向量方法得到求解两个平面夹角的表达式.结合法向量的求解,使学生体验不定方程组的“通解”和“特解”之间的关系,体会一般性寓于特殊性之中的道理.通过对平面与平面的夹角和二面角的辨析,使学生对平面与平面的夹角的理解更加深入.
 3.巩固应用,解决立体几何中的角度问题
3.巩固应用,解决立体几何中的角度问题
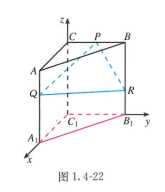
例8 如图1.4-22,在直棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 分别在棱
分别在棱![]() ,
,![]() 上,
上,![]() ,
,![]() .求平面
.求平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
师生活动:教师引导学生先分析题意,明确解题思路,再让学生独立解答,教师根据学生的解答板书补充,其中重点关注法向量的求法.为了保证解题规范,教师展示学生的解答,并适当完善学生板书.
设计意图:通过例题巩固平面与平面所成的角的求解方法,进一步理解法向量的夹角和两个平面所成角的关系,进一步体会向量方法解决立体几何问题的一般步骤.
分析:平面![]() 与平面
与平面![]() 夹角可以转化为
夹角可以转化为
平面![]() 与平面
与平面![]() 法向量的夹角.
法向量的夹角.
解:转化为向量问题
以![]() 为坐标原点,
为坐标原点,![]() 所在直线
所在直线
为![]() 建立空间直角坐标系,设平面
建立空间直角坐标系,设平面![]() 法向量为
法向量为![]() ,平面
,平面![]() 法向量为
法向量为![]() ,平面
,平面![]() 与平面
与平面![]() 夹角即为
夹角即为![]() ,
,![]() 的夹角或其补角.
的夹角或其补角.
进行向量运算
平面![]() 的一个法向量为
的一个法向量为![]() .
.
由题意,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则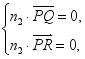 即
即![]()
所以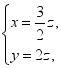 令
令![]() 得
得![]() ,则
,则![]()
回到图形问题
设平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,则
,则![]() ,
,
即平面![]() 与平面
与平面![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
小结:用空间向量解决立体几何问题的“三部曲”:
建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、线、面,把立体几何问题转化为向量问题;
通过向量的运算,研究点、线、面之间的位置关系和它们之间距离、夹角等问题;
把向量运算的结果“翻译”成相应的几何问题.
4.归纳小结
教师引导学生回顾本节课的学习内容,回答下面的问题:
(1)这节课主要学习了哪些内容?
(2)研究这些内容主要用了什么方法?
(3)用向量方法解决立体几何问题的一般步骤是什么?
设计意图:师生共同小结本节课学习的内容和学习过程,通过小结,让学生体会到,直线、平面间的角度刻画了它们的方向的差异,因而可用方向向量或法向量“代表”直线或平面,从而将直线、平面间的角度问题转化为相应的求相应的方向向量、法向量的夹角.进一步体会用向量方法解决立体几何问题的一般步骤.
5.布置作业
教科书习题1.4第9,10题.
五、目标检测设计
教科书![]() 练习第1,2,3,4题.
练习第1,2,3,4题.
设计意图:考查利用向量方法解决直线与直线、直线与平面、平面与平面所成角的能力.
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第3课时教案设计: 这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第3课时教案设计,共9页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
数学选择性必修 第一册1.4 空间向量的应用第1课时教案: 这是一份数学选择性必修 第一册1.4 空间向量的应用第1课时教案,共8页。教案主要包含了教学目标,教学重难点,教学过程,课后作业等内容,欢迎下载使用。
高中数学1.4 空间向量的应用教学设计及反思: 这是一份高中数学1.4 空间向量的应用教学设计及反思,共12页。教案主要包含了教学目标,教学重难点,教学过程,综合应用,解决立体几何问题的方法等内容,欢迎下载使用。













