


高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第3课时教案设计
展开
这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用第3课时教案设计,共9页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
1.4.3用空间向量研究距离、夹角问题(第三课时)(人教A版普通高中教科书数学选择性必修第一册第一章)一、教学目标1.理解利用空间向量解决立体几何问题的三步曲;2.理解解决立体几何问题,可用的三种方法:几何法、向量法、坐标法;3.理解如何求解直线上的相关动点坐标;4.了解用空间向量法解决立体几何问题时,不一定非要建立空间直角坐标系,也可以建立空间基底,或直接进行向量线性运算。二、教学重难点1. 如何让立体几何问题合理转化为向量问题来进行求解;2. 解决立体几何问题时,如何让几何法和向量法综合运用;三、教学过程1.课前练习,复习引入【学生实际情况】经过前面两课时的学习,学生已经懂得运用空间向量法解决空间几何问题,为了温顾知新,简单设计了三个空间立体几何问题的练习,让学生加深理解空间几何与空间向量的关系。【设计意图】创设数学复习情境,让学生感受在数学学习中,基础知识是解决数学问题的重要依据.让学生能熟练运用空间向量来解决空间几何问题。【课前练习】1.已知直线l在平面![]() 外,且
外,且![]() 是直线l的方向向量,
是直线l的方向向量,![]() 是平面
是平面![]() 的法向量,则直线l与平面
的法向量,则直线l与平面![]() 的位置关系为___________.答案:平行关系2.已知直线
的位置关系为___________.答案:平行关系2.已知直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则直线与平面夹角的余弦值为___________.答案:
,则直线与平面夹角的余弦值为___________.答案:![]() 3.已知点
3.已知点![]() 在平面
在平面![]() 内,点
内,点![]() 在平面
在平面![]() 外,若
外,若![]() 是平面
是平面![]() 的法向量,则点
的法向量,则点![]() 到平面
到平面![]() 的距离为___________.答案:32.探究典例,形成应用举例9:如图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为
的距离为___________.答案:32.探究典例,形成应用举例9:如图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为![]() .已知礼物的质量为1kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度?取9.8m/?2,精确到0.01?).【问题预设】问题1:降落伞在匀速下落的过程中,8根绳子拉力的大小总和与礼物重力大小有什么关系?【设计意图】让学生区分力是一个矢量,要看问题研究的对象,如果只讲大小,根据这个力的平衡关系,学生应该能回答8根绳子的拉力大小的总和是大于礼物重力大小.【问题预设】问题2:降落伞在匀速下落的过程中,8根绳子拉力的和与礼物重力有什么关系?【设计意图】问题递进,当问题研究的对象是力的时候,根据这个力的平衡关系,学生应该能回答8根绳子的拉力总和与礼物重力的关系是大小相等,方向相反.【问题预设】问题3:如何用向量方法解决这个问题?【设计意图】研究拉力的合力,就是看作每个向量在竖直方向上的投影向量。其大小就是投影向量的模长。通过这一组问题,能让学生更好的读懂题和准确理解题意.【解题板演】解: 记铅垂线方向的单位向量为
.已知礼物的质量为1kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度?取9.8m/?2,精确到0.01?).【问题预设】问题1:降落伞在匀速下落的过程中,8根绳子拉力的大小总和与礼物重力大小有什么关系?【设计意图】让学生区分力是一个矢量,要看问题研究的对象,如果只讲大小,根据这个力的平衡关系,学生应该能回答8根绳子的拉力大小的总和是大于礼物重力大小.【问题预设】问题2:降落伞在匀速下落的过程中,8根绳子拉力的和与礼物重力有什么关系?【设计意图】问题递进,当问题研究的对象是力的时候,根据这个力的平衡关系,学生应该能回答8根绳子的拉力总和与礼物重力的关系是大小相等,方向相反.【问题预设】问题3:如何用向量方法解决这个问题?【设计意图】研究拉力的合力,就是看作每个向量在竖直方向上的投影向量。其大小就是投影向量的模长。通过这一组问题,能让学生更好的读懂题和准确理解题意.【解题板演】解: 记铅垂线方向的单位向量为![]() ,设每根绳子的拉力为
,设每根绳子的拉力为![]() , 因为
, 因为![]() =
=![]() , 所以向量
, 所以向量![]() 在向量
在向量![]() 上的投影向量为:
上的投影向量为:![]()
![]() 由于8根绳子的合力大小与礼物重力大小相等,所以
由于8根绳子的合力大小与礼物重力大小相等,所以 ![]() ,所以
,所以![]() 即:降落伞在匀速下落的过程中每根绳子拉力的大小是
即:降落伞在匀速下落的过程中每根绳子拉力的大小是![]() .
. 【设计意图】规范解题,作好学生的示范.特别强调先设向量,再把实际问题转化为向量问题来求解,最后回答实际问题。
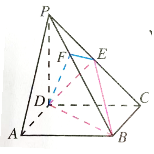
【设计意图】规范解题,作好学生的示范.特别强调先设向量,再把实际问题转化为向量问题来求解,最后回答实际问题。 举例10:如图,在四棱锥
举例10:如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱PD
中,底面ABCD是正方形,侧棱PD![]() 底面ABCD,PD=DC, E是PC的中点,作EF
底面ABCD,PD=DC, E是PC的中点,作EF ![]() PB交PB于点F.
PB交PB于点F.![]() 求证:PA
求证:PA![]() 平面EDB ;(2)求证:PB
平面EDB ;(2)求证:PB ![]() 平面EFD ;(3)求平面CPB与平面PBD的夹角的大小. 【问题预设】问题1:线面平行的几何法证明思路是怎么样分析得到的?学生容易想到,如图作辅助线,从而利用三角形中位线来证明:PA
平面EFD ;(3)求平面CPB与平面PBD的夹角的大小. 【问题预设】问题1:线面平行的几何法证明思路是怎么样分析得到的?学生容易想到,如图作辅助线,从而利用三角形中位线来证明:PA![]() EG问题2:线面平行的向量法证明思路又是怎么样呢?也可以利用向量知识,先建立空间坐标系,再来证明:
EG问题2:线面平行的向量法证明思路又是怎么样呢?也可以利用向量知识,先建立空间坐标系,再来证明:![]()
![]() 也可以直接证明
也可以直接证明![]() 与平面EDB的法向量垂直,从而得到线面平行.【设计意图】立体几何问题,首先想想利用掌握的空间关系来试证明,若能完成,则用几何法解决问题,若不能完成,则考虑向量法来补充证明。【解题板演】证明:(1)连接AC交BD于点G,再连接EG, 由正方形ABCD可得:AG=GC 又因为E是PC的中点, 所以PA
与平面EDB的法向量垂直,从而得到线面平行.【设计意图】立体几何问题,首先想想利用掌握的空间关系来试证明,若能完成,则用几何法解决问题,若不能完成,则考虑向量法来补充证明。【解题板演】证明:(1)连接AC交BD于点G,再连接EG, 由正方形ABCD可得:AG=GC 又因为E是PC的中点, 所以PA ![]() EG , 又因为PA
EG , 又因为PA![]() , EG
, EG![]() 所以PA
所以PA![]() 平面EDB 【设计意图】第一问还是采用几何法证明简单,没必要转化为向量法来证明,所以只设计了几何法证明的答案,向量法只了解一下思路。我们还是追求数学的简洁美。 【问题预设】问题3:线面垂直的几何法证明思路是怎么样分析得到的?学生能够回答,要证明PB
平面EDB 【设计意图】第一问还是采用几何法证明简单,没必要转化为向量法来证明,所以只设计了几何法证明的答案,向量法只了解一下思路。我们还是追求数学的简洁美。 【问题预设】问题3:线面垂直的几何法证明思路是怎么样分析得到的?学生能够回答,要证明PB ![]() 平面EFD , 由于PB
平面EFD , 由于PB![]() EF , 所以只需要证明PB
EF , 所以只需要证明PB![]() DE 或PB
DE 或PB![]() DF.问题4:发现几何法证明线线垂直有点麻烦,若用向量法怎么样才能证明呢?此时发现利用向量知识,很容易证明: PB
DF.问题4:发现几何法证明线线垂直有点麻烦,若用向量法怎么样才能证明呢?此时发现利用向量知识,很容易证明: PB![]() DE,即证明
DE,即证明![]() 【设计意图】立体几何问题,首先还是想想利用掌握的空间关系来试证明,若某个环节不能完成证明的时候,则考虑向量法来补充证明。【解题板演】证明:(2)以D为原点,DA, DC, DP 所在的直线分别为
【设计意图】立体几何问题,首先还是想想利用掌握的空间关系来试证明,若某个环节不能完成证明的时候,则考虑向量法来补充证明。【解题板演】证明:(2)以D为原点,DA, DC, DP 所在的直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,
轴,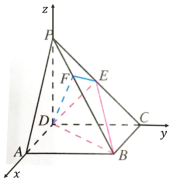 如图建立坐标系,设DC=1,则依题意得:A(1,0,0) , P(0,0,1), C(0,1,0), B(1,1,0), E(0,
如图建立坐标系,设DC=1,则依题意得:A(1,0,0) , P(0,0,1), C(0,1,0), B(1,1,0), E(0,![]() ,
, ![]() ).
). ![]() 故
故![]() 所以
所以![]() 由已知EF
由已知EF ![]() PB,且
PB,且![]() 所以PB
所以PB ![]() 平面EFD .【问题预设】问题5:求二面角的几何法证明思路是怎么样分析得到的?如图,由于PB
平面EFD .【问题预设】问题5:求二面角的几何法证明思路是怎么样分析得到的?如图,由于PB ![]() 平面EFD , 所以
平面EFD , 所以![]() 此时发现几何法求这个角有难度,但利用向量知识,很容易想到用向量
此时发现几何法求这个角有难度,但利用向量知识,很容易想到用向量![]() 夹角来求
夹角来求![]() 的大小.问题6:用向量思想来求向量夹角,但是如何求出点F 的空间坐标?如图,要研究点的坐标,可以用设未知数的方法,来找到点
的大小.问题6:用向量思想来求向量夹角,但是如何求出点F 的空间坐标?如图,要研究点的坐标,可以用设未知数的方法,来找到点![]() 满足的相关条件,然后求出这个点的坐标,从而利用向量方法解决二面角问题.【设计意图】立体几何问题,首先还是想想利用掌握的空间关系来试证明,若某个环节不能完成求解的时候,则考虑向量法来补充求解。【解题板演】
满足的相关条件,然后求出这个点的坐标,从而利用向量方法解决二面角问题.【设计意图】立体几何问题,首先还是想想利用掌握的空间关系来试证明,若某个环节不能完成求解的时候,则考虑向量法来补充求解。【解题板演】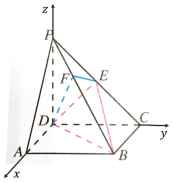 (3)由(2)得PB
(3)由(2)得PB ![]() 平面EFD , PB
平面EFD , PB ![]() EF, PB
EF, PB ![]() DF , 所以
DF , 所以![]() 设点F
设点F![]() 坐标为
坐标为![]() ,则
,则![]() ,因为EF
,因为EF ![]() PB且交PB于点F, 所以
PB且交PB于点F, 所以![]()
![]() , 所以
, 所以![]() 又由
又由![]() 所以
所以![]() 所以
所以 ![]()
![]() 即cos
即cos![]() 所以
所以![]() 即平面CPB与平面PBD的夹角的大小为
即平面CPB与平面PBD的夹角的大小为![]() 【学习要求】懂得如何求出直线上动点的坐标,再用向量的坐标运算解决几何问题。
【学习要求】懂得如何求出直线上动点的坐标,再用向量的坐标运算解决几何问题。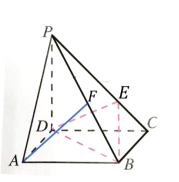 3.例题变式,提高能力变式1:如图,在四棱锥
3.例题变式,提高能力变式1:如图,在四棱锥![]() 中,底面ABCD是正方形,侧棱PD
中,底面ABCD是正方形,侧棱PD![]() 底面ABCD,PD=DC, E是PC的三等分点,且PE=2EC.
底面ABCD,PD=DC, E是PC的三等分点,且PE=2EC.![]() PB上是否存在点F ,使得AF
PB上是否存在点F ,使得AF![]() 平面EDB ,若存在,求出BF: PB的值 ;若不存在,请说明理由.【问题预设】问题1:此题用几何法研究线线平行有点难度,但转化为向量法研究线面平行,容易想到研究什么向量?如图,可以研究线向量
平面EDB ,若存在,求出BF: PB的值 ;若不存在,请说明理由.【问题预设】问题1:此题用几何法研究线线平行有点难度,但转化为向量法研究线面平行,容易想到研究什么向量?如图,可以研究线向量![]() 与平面BDE的法向量
与平面BDE的法向量![]() 之间的垂直关系。问题2:用向量思想来解此题,关键是如何求出点F 的空间坐标?此时和刚才例题一样,利用设坐标的思想,通过三点共线得到其中两条向量共线,从而找到坐标之间的关系.
之间的垂直关系。问题2:用向量思想来解此题,关键是如何求出点F 的空间坐标?此时和刚才例题一样,利用设坐标的思想,通过三点共线得到其中两条向量共线,从而找到坐标之间的关系.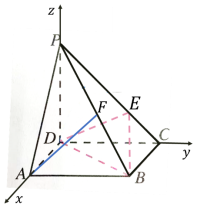 【设计意图】从感知个例到分析通例,遵循从特殊到一般的思路,在具体问题实践的基础上提高能力,认识直线上的动点是如何用坐标来研究并解决问题的,为以后提升空间几何问题的解题能力作铺垫.【解题板演】解:以D为原点,DA, DC, DP 所在的直线分别为
【设计意图】从感知个例到分析通例,遵循从特殊到一般的思路,在具体问题实践的基础上提高能力,认识直线上的动点是如何用坐标来研究并解决问题的,为以后提升空间几何问题的解题能力作铺垫.【解题板演】解:以D为原点,DA, DC, DP 所在的直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,如图建立坐标系,设DC=1,则依题意得:A(1,0,0) , P(0,0,1), C(0,1,0), B(1,1,0), E(0,
轴,如图建立坐标系,设DC=1,则依题意得:A(1,0,0) , P(0,0,1), C(0,1,0), B(1,1,0), E(0,![]() ,
, ![]() ).
). ![]() 设平面
设平面![]()
 ,
,![]() 所以
所以![]() ,又设
,又设![]()
![]() , 所以
, 所以![]() 因为要满足AF
因为要满足AF![]() 平面EDB ,
平面EDB ,![]()
![]()
![]() ,
,![]()
![]() PF: PB的值是
PF: PB的值是![]() .4.探究典例,形成应用
.4.探究典例,形成应用 例11:如图,二面角
例11:如图,二面角![]() 的棱上有两个点A,B,线段BD与AC分别在这个二面角的两个平面内,并且都垂直于棱
的棱上有两个点A,B,线段BD与AC分别在这个二面角的两个平面内,并且都垂直于棱![]() 。若AB=4,AC=6,BD=8, CD =
。若AB=4,AC=6,BD=8, CD =![]() , 求平面
, 求平面![]() 与平面
与平面![]() 的夹角.【问题预设】问题1:此题二面角的几何法求解思路是怎么样的?
的夹角.【问题预设】问题1:此题二面角的几何法求解思路是怎么样的?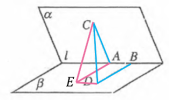 如图,可以作
如图,可以作![]() ,连接CE. 二面角
,连接CE. 二面角![]() 的平面角就是
的平面角就是![]() 但是容易发现这个角所在的三角形有一条边
但是容易发现这个角所在的三角形有一条边![]() 不好求边长.问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解?
不好求边长.问题2:此题二面角的几何法求解思路受阻,请问转换空间向量思想如何来求解?![]() 思考向量方法,发现二面角
思考向量方法,发现二面角![]() 的大小就是
的大小就是![]() 最后,我们
最后,我们![]() 而我们想到这里有四条线段长全部已知,要求角大小,可以利用向量模与数量积的关系来求解【解题板演】
而我们想到这里有四条线段长全部已知,要求角大小,可以利用向量模与数量积的关系来求解【解题板演】![]()
![]()
![]() 又因为AB=4,AC=6,BD=8, CD =
又因为AB=4,AC=6,BD=8, CD =![]()
![]()
![]() ,
,![]()
![]() ,所以平面
,所以平面![]() 与平面
与平面![]() 的夹角是
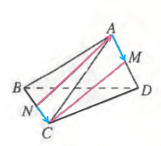
的夹角是![]() .【设计意图】(1)几何法有困难,向量法又不好建系,也就想到向量的基底法或线性运算法来求夹角大小.(2)懂得当已知首尾连接的四条线段长时,又知道其中两组相邻边的夹角,就可以求相对两边所成的角. 5.习题变式,形成技能P41页练习2:如图,在三棱锥A-BCD中,AB=AC=BD=CD=3, AD=BC=2, M, N分别是AD,BC的中点. 求异面直线AN与CM所成角的余弦值.
.【设计意图】(1)几何法有困难,向量法又不好建系,也就想到向量的基底法或线性运算法来求夹角大小.(2)懂得当已知首尾连接的四条线段长时,又知道其中两组相邻边的夹角,就可以求相对两边所成的角. 5.习题变式,形成技能P41页练习2:如图,在三棱锥A-BCD中,AB=AC=BD=CD=3, AD=BC=2, M, N分别是AD,BC的中点. 求异面直线AN与CM所成角的余弦值.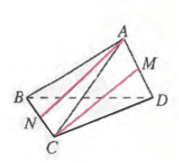 【问题预设】问题1:此题与书中例7相类似,肯定可以用书中方法来求解。但是除此方法外,是否由前面例题的解题思想总结出来
【问题预设】问题1:此题与书中例7相类似,肯定可以用书中方法来求解。但是除此方法外,是否由前面例题的解题思想总结出来 的经验来解此题,请问求解的思路是怎么样的? 根据经验总结,可以选择一条向量用其它三条向量来线性表示,并且这四条向量的模长都是已知的,而且能已知两组相邻边的夹角。问题2:这里的每两条向量的数量积分别怎么计算?
的经验来解此题,请问求解的思路是怎么样的? 根据经验总结,可以选择一条向量用其它三条向量来线性表示,并且这四条向量的模长都是已知的,而且能已知两组相邻边的夹角。问题2:这里的每两条向量的数量积分别怎么计算?![]()
![]()
![]()
![]()
 【解题板演】
【解题板演】![]()
![]()
![]()
![]()
 所以异面直线AN与CM所成角的余弦值是
所以异面直线AN与CM所成角的余弦值是![]() .
.![]()
![]()
![]()
![]() 所以异面直线AN与CM所成角的余弦值是
所以异面直线AN与CM所成角的余弦值是![]() .【设计意图】此题利用向量法,一题多解,除了课本上的方法外,还补充验证了向量法求异面直线所成角的思路,针对这一类题型既要总结到位,又要娴熟应用。6.课堂小结,强调重点1、通过这节课的学习,我们对立体几何中的向量法是否有了新的认识?
.【设计意图】此题利用向量法,一题多解,除了课本上的方法外,还补充验证了向量法求异面直线所成角的思路,针对这一类题型既要总结到位,又要娴熟应用。6.课堂小结,强调重点1、通过这节课的学习,我们对立体几何中的向量法是否有了新的认识?![]()
![]()
![]() ,从而解决问题。以上就是利用向量法解决立体几何问题的三步曲。2、相信通过这节课的学习,我们已经提高了应用向量知识来解决综合性较强的立体几何问题的能力。
,从而解决问题。以上就是利用向量法解决立体几何问题的三步曲。2、相信通过这节课的学习,我们已经提高了应用向量知识来解决综合性较强的立体几何问题的能力。![]() 特别是对直线上的动点研究及其运算方法;
特别是对直线上的动点研究及其运算方法;![]() 就是利用四条线段的长及相邻两边夹角大小来求异面直线所成的角的大小。【设计意图】(1)突出本节课的重点,利用向量法解题的三步曲;(2)加强本节课对于向量法求解立体几何问题的新认知,即向量法解题可以建系用坐标运算法,也可以不建系用基底运算法,还可以用线性运算和数量积运算;(3)突出求直线上动点的运算方法和求异面直线所成角的方法。7.课外作业,巩固提高
就是利用四条线段的长及相邻两边夹角大小来求异面直线所成的角的大小。【设计意图】(1)突出本节课的重点,利用向量法解题的三步曲;(2)加强本节课对于向量法求解立体几何问题的新认知,即向量法解题可以建系用坐标运算法,也可以不建系用基底运算法,还可以用线性运算和数量积运算;(3)突出求直线上动点的运算方法和求异面直线所成角的方法。7.课外作业,巩固提高![]()
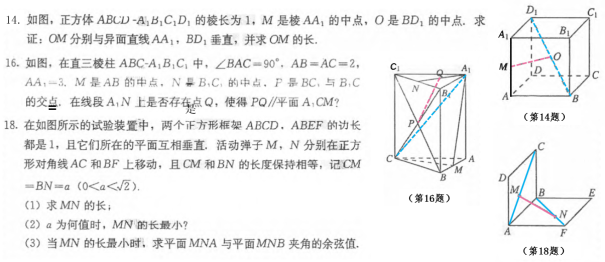 【设计意图】(1)第14题突出直线上的动点研究;(2)第16题是突出例题10的变式应用;(3)第18题突出直线上的动点研究,及二面角的向量法求解。
【设计意图】(1)第14题突出直线上的动点研究;(2)第16题是突出例题10的变式应用;(3)第18题突出直线上的动点研究,及二面角的向量法求解。
相关教案
这是一份高中人教A版 (2019)1.4 空间向量的应用第2课时教学设计及反思,共5页。教案主要包含了教学内容,教学目标,教学重点与难点,教学过程设计,目标检测设计等内容,欢迎下载使用。
这是一份数学选择性必修 第一册1.4 空间向量的应用第1课时教案,共8页。教案主要包含了教学目标,教学重难点,教学过程,课后作业等内容,欢迎下载使用。
这是一份高中数学1.4 空间向量的应用教学设计及反思,共12页。教案主要包含了教学目标,教学重难点,教学过程,综合应用,解决立体几何问题的方法等内容,欢迎下载使用。










