


2022-2023学年山东省济南市礼乐初级中学七下数学期末综合测试试题含答案
展开
这是一份2022-2023学年山东省济南市礼乐初级中学七下数学期末综合测试试题含答案,共8页。试卷主要包含了下列事件中必然事件有等内容,欢迎下载使用。
2022-2023学年山东省济南市礼乐初级中学七下数学期末综合测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题(每小题3分,共30分)1.已知点A(﹣2,y1),点B(﹣4,y2)在直线y=﹣2x+3上,则( )A.y1>y2 B.y1=y2 C.y1<y2 D.无法比较2.下列各式中,正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.在如图所示的正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果 C也是图中的格点,且使得△ABC为等腰直角三角形,则这样的点C有( )
3.在如图所示的正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果 C也是图中的格点,且使得△ABC为等腰直角三角形,则这样的点C有( )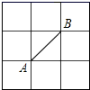 A.6个 B.7个 C.8个 D.9个4.如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( )
A.6个 B.7个 C.8个 D.9个4.如图,在平行四边形ABCD中,用直尺和圆规作的∠BAD平分线交BC于点E,若AE=8,AB=5,则BF的长为( ) 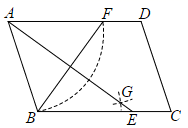 A.4 B.5 C.6 D.85.如图,直线
A.4 B.5 C.6 D.85.如图,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )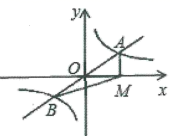 A.2 B.4 C.-2 D.-46.下列事件中必然事件有( )①当x是非负实数时,
A.2 B.4 C.-2 D.-46.下列事件中必然事件有( )①当x是非负实数时,![]() ≥0;②打开数学课本时刚好翻到第12页;③13个人中至少有2人的生日是同一个月;④在一个只装有白球和绿球的袋中摸球,摸出黑球.A.1个 B.2个 C.3个 D.4个7.下列各式由左到右的变形中,属于分解因式的是( )A.
≥0;②打开数学课本时刚好翻到第12页;③13个人中至少有2人的生日是同一个月;④在一个只装有白球和绿球的袋中摸球,摸出黑球.A.1个 B.2个 C.3个 D.4个7.下列各式由左到右的变形中,属于分解因式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连结EF,若AB=6,BC=4
8.如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连结EF,若AB=6,BC=4![]() ,则FD的长为( )
,则FD的长为( )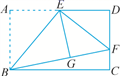 A.2 B.4 C.
A.2 B.4 C.![]() D.2
D.2![]() 9.函数y=mx+n与y=nx的大致图象是( )A.
9.函数y=mx+n与y=nx的大致图象是( )A.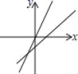 B.
B.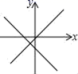 C.
C.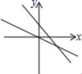 D.
D.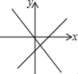 10.弹簧挂上物体后伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:下列说法错误的是( )物体的质量(kg)012345弹簧的长度(cm)1012.51517.52022.5A.在没挂物体时,弹簧的长度为10cmB.弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量C.如果物体的质量为mkg,那么弹簧的长度ycm可以表示为y=2.5m+10D.在弹簧能承受的范围内,当物体的质量为4kg时,弹簧的长度为20cm二、填空题(本大题共有6小题,每小题3分,共18分)11.每本书的厚度为0.62cm,把这些书摞在一起总厚度h(单位:cm)随书的本数n的变化而变化,请写出h关于n的函数解析式_____.12.如图,在平面直角坐标系xOy中,A是双曲线
10.弹簧挂上物体后伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:下列说法错误的是( )物体的质量(kg)012345弹簧的长度(cm)1012.51517.52022.5A.在没挂物体时,弹簧的长度为10cmB.弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量C.如果物体的质量为mkg,那么弹簧的长度ycm可以表示为y=2.5m+10D.在弹簧能承受的范围内,当物体的质量为4kg时,弹簧的长度为20cm二、填空题(本大题共有6小题,每小题3分,共18分)11.每本书的厚度为0.62cm,把这些书摞在一起总厚度h(单位:cm)随书的本数n的变化而变化,请写出h关于n的函数解析式_____.12.如图,在平面直角坐标系xOy中,A是双曲线![]() 在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。(1)点C与原点O的最短距离是________;(2)没点C的坐标为(
在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。(1)点C与原点O的最短距离是________;(2)没点C的坐标为(![]() ,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。
,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。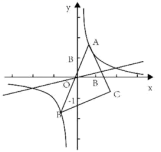 13.据统计,2019年全国高考报名人数达10310000人,比去年增加了560000,其中数据10310000用科学计数法表示为_________14.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(2,1),过点E的直线与BC交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为________.
13.据统计,2019年全国高考报名人数达10310000人,比去年增加了560000,其中数据10310000用科学计数法表示为_________14.如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(2,1),过点E的直线与BC交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为________. 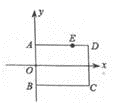 15.如图所示四个二次函数的图象中,分别对应的是①y=ax1;②y=bx1;③y=cx1;④y=dx1.则a、b、c、d的大小关系为_____.
15.如图所示四个二次函数的图象中,分别对应的是①y=ax1;②y=bx1;③y=cx1;④y=dx1.则a、b、c、d的大小关系为_____.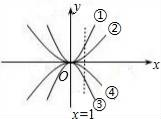 16.如图,在平面直角坐标系中,▱ABCD的顶点坐标分别为A(3,a)、B(2,2)、C(b,3)、D(8,6),则a+b的值为_____.
16.如图,在平面直角坐标系中,▱ABCD的顶点坐标分别为A(3,a)、B(2,2)、C(b,3)、D(8,6),则a+b的值为_____.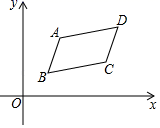 三、解下列各题(本大题共8小题,共72分)17.(8分)根据要求,解答下列问题.(1)根据要求,解答下列问题.①方程x2-2x+1=0的解为________________________;②方程x2-3x+2=0的解为________________________;③方程x2-4x+3=0的解为________________________;…… ……(2)根据以上方程特征及其解的特征,请猜想:①方程x2-9x+8=0的解为________________________;②关于x的方程________________________的解为x1=1,x2=n.(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性. 18.(8分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.
三、解下列各题(本大题共8小题,共72分)17.(8分)根据要求,解答下列问题.(1)根据要求,解答下列问题.①方程x2-2x+1=0的解为________________________;②方程x2-3x+2=0的解为________________________;③方程x2-4x+3=0的解为________________________;…… ……(2)根据以上方程特征及其解的特征,请猜想:①方程x2-9x+8=0的解为________________________;②关于x的方程________________________的解为x1=1,x2=n.(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性. 18.(8分)如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C 重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD. 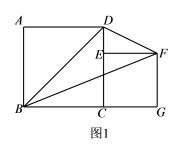
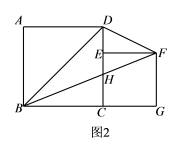 (1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为
(1)当点E与点D重合时,△BDF的面积为 ;当点E为CD的中点时,△BDF的面积为 .(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想; (3)如图2,设BF与CD相交于点H,若△DFH的面积为![]() ,求正方形CEFG的边长. 19.(8分)如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,求正方形CEFG的边长. 19.(8分)如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).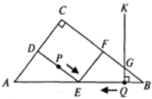 (1)D,F两点间的距离是 ;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;(3)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;(4)连结PG,当PG∥AB时,请直接写出t的值. 20.(8分)解不等式组:
(1)D,F两点间的距离是 ;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;(3)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;(4)连结PG,当PG∥AB时,请直接写出t的值. 20.(8分)解不等式组:![]() ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。![]() 21.(8分)已知函数
21.(8分)已知函数![]() .(1)若函数图象经过原点,求
.(1)若函数图象经过原点,求![]() 的值;(2)若这个函数是一次函数,且
的值;(2)若这个函数是一次函数,且![]() 随着
随着![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围. 22.(10分)某乡镇组织300名干部、群众参加义务植树活动,下表是随机抽出的50名干部、群众义务植树的统计,根据图中的数据回答下列问题:植树棵树34568人数8151278(1)这50个人平均每人植树多少棵?植树棵数的中位数是多少?(2)估计该乡镇本次活动共植树多少棵? 23.(10分)如图正比例函数y=2x的图像与一次函数
的取值范围. 22.(10分)某乡镇组织300名干部、群众参加义务植树活动,下表是随机抽出的50名干部、群众义务植树的统计,根据图中的数据回答下列问题:植树棵树34568人数8151278(1)这50个人平均每人植树多少棵?植树棵数的中位数是多少?(2)估计该乡镇本次活动共植树多少棵? 23.(10分)如图正比例函数y=2x的图像与一次函数 ![]() 的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.(1)求一次函数的解析式; (2)求
的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.(1)求一次函数的解析式; (2)求![]() 的面积.
的面积.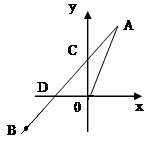 24.(12分)某中学需要添置一批教学仪器,方案一:到厂家购买,每件原价40元,恰逢厂家促销活动八折出售;方案二学校自己制作,每件20元,另外需要制作工具的租用费600元;设该学校需要购买仪器x件,方案一与方案二的费用分别为y1和y2(元)(1)请分别求出y1,y2关于x的函数表达式;(2)若学校需要购买仪器30~60(含30和60)件,问采用哪种方案更划算?请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、C5、A6、B7、C8、B9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、h=0.62n12、
24.(12分)某中学需要添置一批教学仪器,方案一:到厂家购买,每件原价40元,恰逢厂家促销活动八折出售;方案二学校自己制作,每件20元,另外需要制作工具的租用费600元;设该学校需要购买仪器x件,方案一与方案二的费用分别为y1和y2(元)(1)请分别求出y1,y2关于x的函数表达式;(2)若学校需要购买仪器30~60(含30和60)件,问采用哪种方案更划算?请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、C5、A6、B7、C8、B9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、h=0.62n12、![]()
![]() 13、1.031×114、y=2x-3.15、a>b>d>c16、12 三、解下列各题(本大题共8小题,共72分)17、(1)①x1=1,x2=1;②x1=1,x2=2;③x1=1,x2=1.(2)①x1=1,x2=2, ②x2-(1+n)x+n=3;(1)x1=1,x2=2.18、(1)1,1;(2)S△BDF=
13、1.031×114、y=2x-3.15、a>b>d>c16、12 三、解下列各题(本大题共8小题,共72分)17、(1)①x1=1,x2=1;②x1=1,x2=2;③x1=1,x2=1.(2)①x1=1,x2=2, ②x2-(1+n)x+n=3;(1)x1=1,x2=2.18、(1)1,1;(2)S△BDF=![]() S正方形ABCD,证明见解析;(3)219、(1)25;(2)能,t=
S正方形ABCD,证明见解析;(3)219、(1)25;(2)能,t=![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() 和
和![]() 20、
20、![]() ,解集在数轴上表示见解析21、(1)
,解集在数轴上表示见解析21、(1)![]() ,(2)
,(2)![]() .22、(1)5,5;(2)1500.23、(1)一次函数的解析式为
.22、(1)5,5;(2)1500.23、(1)一次函数的解析式为![]() ;(2)1.24、(1)y1=32x,y2=20x+600;(2)30≤x<50时,方案一划算.
;(2)1.24、(1)y1=32x,y2=20x+600;(2)30≤x<50时,方案一划算.
相关试卷
这是一份2023-2024学年山东省济南市礼乐初级中学数学九上期末达标检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,对于方程,下列说法正确的是,P关于原点对称的点的坐标是等内容,欢迎下载使用。
这是一份山东省济南市礼乐初级中学2023-2024学年八上数学期末预测试题含答案,共7页。试卷主要包含了等式0=1成立的条件是,下列五个命题中,真命题有等内容,欢迎下载使用。
这是一份武汉广雅初级中学2022-2023学年数学七下期末综合测试模拟试题含答案,共5页。试卷主要包含了若,则的值,化简的结果是,已知不等式组的解集如图所示等内容,欢迎下载使用。








