


2022-2023学年山东省济南长清区六校联考七年级数学第二学期期末达标测试试题含答案
展开
这是一份2022-2023学年山东省济南长清区六校联考七年级数学第二学期期末达标测试试题含答案,共8页。试卷主要包含了下列方程有两个相等的实数根的是等内容,欢迎下载使用。
2022-2023学年山东省济南长清区六校联考七年级数学第二学期期末达标测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗. 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F,若四边形DCFE的周长为18cm,AC的长6cm,则AD的长为( )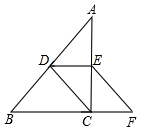 A.13cm B.12cm C.5cm D.8cm2.如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于点D,交AB于点E,下列叙述结论错误的是( )
A.13cm B.12cm C.5cm D.8cm2.如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于点D,交AB于点E,下列叙述结论错误的是( )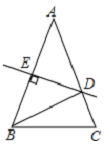 A.BD平分∠ABC B.△BCD的周长等于AB+BCC.点D是线段AC的中点 D.AD=BD=BC3.下列分式的运算中,其中正确的是( )A.
A.BD平分∠ABC B.△BCD的周长等于AB+BCC.点D是线段AC的中点 D.AD=BD=BC3.下列分式的运算中,其中正确的是( )A.![]() B.
B.![]() =
=![]() C.
C.![]() =a+b D.
=a+b D.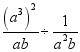 =a54. 炎炎夏日,甲安装队为A小区安装88台空调,乙安装队为B小区安装80台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台,设乙队每天安装x台,根据题意,下面所列方程正确的是( )A.
=a54. 炎炎夏日,甲安装队为A小区安装88台空调,乙安装队为B小区安装80台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台,设乙队每天安装x台,根据题意,下面所列方程正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.若平行四边形的两个内角的度数之比为1:5,则其中较小的内角是( )A.
5.若平行四边形的两个内角的度数之比为1:5,则其中较小的内角是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.一组数据3、-2、0、1、4的中位数是( )A.0 B.1 C.-2 D.47.下列从左到右的变形是分解因式的是( )A.
6.一组数据3、-2、0、1、4的中位数是( )A.0 B.1 C.-2 D.47.下列从左到右的变形是分解因式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.某中学随机调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:时间
8.某中学随机调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:时间![]() 小时5678人数10102010则这50名学生这一周在校的平均体育锻炼时间是
小时5678人数10102010则这50名学生这一周在校的平均体育锻炼时间是![]()
![]() A.
A.![]() 小时 B.
小时 B.![]() 小时 C.
小时 C.![]() 小时 D.7小时9.如图,一个长为2、宽为1的长方形以下面的“姿态”从直线
小时 D.7小时9.如图,一个长为2、宽为1的长方形以下面的“姿态”从直线![]() 的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( )
的左侧水平平移至右侧(下图中的虚线是水平线),其中,平移的距离是( )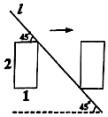 A.1 B.2 C.3 D.
A.1 B.2 C.3 D.![]() 10.下列方程有两个相等的实数根的是( )A.
10.下列方程有两个相等的实数根的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )
11.某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )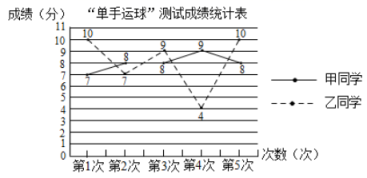 A.甲成绩的平均分低于乙成绩的平均分;B.甲成绩的中位数高于乙成绩的中位数;C.甲成绩的众数高于乙成绩的众数;D.甲成绩的方差低于乙成绩的方差.12.从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组
A.甲成绩的平均分低于乙成绩的平均分;B.甲成绩的中位数高于乙成绩的中位数;C.甲成绩的众数高于乙成绩的众数;D.甲成绩的方差低于乙成绩的方差.12.从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组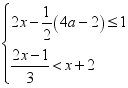 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )A.
=1有非负整数解的概率是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在⊙O中,AC为直径,过点O作OD⊥AB于点E,交⊙O于点D,连接BC,若AB=
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在⊙O中,AC为直径,过点O作OD⊥AB于点E,交⊙O于点D,连接BC,若AB=![]() ,ED=
,ED=![]() ,则BC=_____.
,则BC=_____.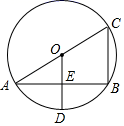 14.方程
14.方程![]() x4-8=0的根是______15.某校生物小组7人到校外采集标本,其中2人每人采集到3件,3人每人采集到4件,2人每人采集到5件,则这个小组平均每人采集标本___________件.16.如图,平行四边形
x4-8=0的根是______15.某校生物小组7人到校外采集标本,其中2人每人采集到3件,3人每人采集到4件,2人每人采集到5件,则这个小组平均每人采集标本___________件.16.如图,平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,点
上一动点,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.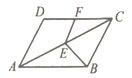 17.如图,直线
17.如图,直线![]() 经过点
经过点![]() 和点
和点![]() ,直线
,直线![]() 经过点
经过点![]() ,则不等式组
,则不等式组![]() 的解集是______.
的解集是______.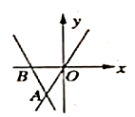 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,菱形
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,菱形![]() 的对角线
的对角线![]() 和
和![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的长.
的长.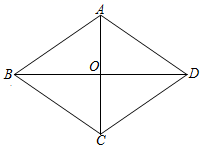 19.(5分)探究:如图,在正方形
19.(5分)探究:如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() .
.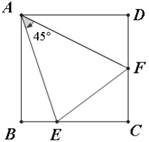 (1)如果将
(1)如果将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() .请你画出图形(旋转后的辅助线).你能够得出关于
.请你画出图形(旋转后的辅助线).你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.(2)如果点
的一个结论是________.(2)如果点![]() ,
,![]() 分别运动到
分别运动到![]() ,
,![]() 的延长线上,如图,请你能够得出关于
的延长线上,如图,请你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.
的一个结论是________.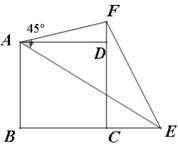 (3)变式:如图,将题目改为“在四边形
(3)变式:如图,将题目改为“在四边形![]() 中,
中,![]() ,且
,且![]() ,点
,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() ”,请你猜想关于
”,请你猜想关于![]() ,
,![]() ,
,![]() 有什么关系?并验证你的猜想.
有什么关系?并验证你的猜想.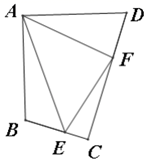 20.(8分)某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
20.(8分)某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: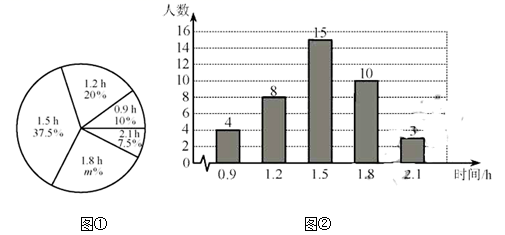 (Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数. 21.(10分)如图,已知直线
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数. 21.(10分)如图,已知直线![]() 经过点
经过点![]() ,交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.
,交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.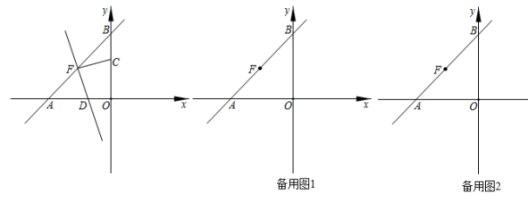
![]() 当
当![]() 时,求证:
时,求证:![]() ;
;![]() 连接CD,若
连接CD,若![]() 的面积为S,求出S与t的函数关系式;
的面积为S,求出S与t的函数关系式;![]() 在运动过程中,直线CF交x轴的负半轴于点G,
在运动过程中,直线CF交x轴的负半轴于点G,![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由. 22.(10分)上合组织峰会期间,甲、乙两家商场都将平时以同样价格出售相同的商品进行让利酬宾,其中甲商场所有商品按7折出售,乙商场对一次购物中超过200元后的价格部分打6折.(1)以x(单位:元)表示商品原价,y(单位:元)表示付款金额,分别就两家商场的让利方式写出y与x之间的函数解析式;(2)上合组织峰会期问如何选择这两家商场去购物更省钱? 23.(12分)已知一次函数
是否为定值?若是,请求出这个定值;若不是,请说明理由. 22.(10分)上合组织峰会期间,甲、乙两家商场都将平时以同样价格出售相同的商品进行让利酬宾,其中甲商场所有商品按7折出售,乙商场对一次购物中超过200元后的价格部分打6折.(1)以x(单位:元)表示商品原价,y(单位:元)表示付款金额,分别就两家商场的让利方式写出y与x之间的函数解析式;(2)上合组织峰会期问如何选择这两家商场去购物更省钱? 23.(12分)已知一次函数![]() .
.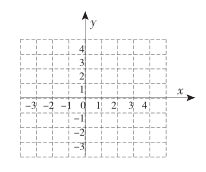 (1)画出该函数的图象;(2)若该函数图象与
(1)画出该函数的图象;(2)若该函数图象与![]() 轴,
轴,![]() 轴分別交于
轴分別交于![]() 、
、![]() 两点,求
两点,求![]() 、
、![]() 两点的坐标. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、B4、D5、A6、B7、C8、C9、C10、B11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
两点的坐标. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、C3、B4、D5、A6、B7、C8、C9、C10、B11、D12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、±215、416、
14、±215、416、![]() 17、
17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、![]() 19、(1)EF=BE+DF,画图如图所示;(2)BE= DF+EF;(3)EF=BE+DF,理由见解析20、(Ⅰ)40,1;(Ⅱ)平均数是1.2,众数为1.2,中位数为1.2;(Ⅲ)每天在校体育活动时间大于1h的学生人数约为3.21、(1)见解析;(2)
19、(1)EF=BE+DF,画图如图所示;(2)BE= DF+EF;(3)EF=BE+DF,理由见解析20、(Ⅰ)40,1;(Ⅱ)平均数是1.2,众数为1.2,中位数为1.2;(Ⅲ)每天在校体育活动时间大于1h的学生人数约为3.21、(1)见解析;(2)![]() ;(3)
;(3)![]() .22、(1)甲商场:y=0.7x,乙商场:当0≤x≤200时,y=x,当x>200时,y=200+0.6(x﹣200)=0.6x+80;(2)当x<800时,在甲商场购买比较省钱,当x=800时,在甲乙两商场购买花钱一样,当x>800时,在乙商场购买省钱.23、(1)答案见解析;(2)
.22、(1)甲商场:y=0.7x,乙商场:当0≤x≤200时,y=x,当x>200时,y=200+0.6(x﹣200)=0.6x+80;(2)当x<800时,在甲商场购买比较省钱,当x=800时,在甲乙两商场购买花钱一样,当x>800时,在乙商场购买省钱.23、(1)答案见解析;(2)![]() ,
,![]() .
.
相关试卷
这是一份山东省济南长清区六校联考2023-2024学年九年级数学第一学期期末教学质量检测模拟试题含答案,共8页。
这是一份2023-2024学年山东省济南长清区六校联考八年级数学第一学期期末经典试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列说法正确的是,关于x的方程有增根则a=,的绝对值是等内容,欢迎下载使用。
这是一份山东省济南章丘区五校联考2022-2023学年七年级数学第二学期期末监测试题含答案,共6页。试卷主要包含了已知,则下列结论正确的是等内容,欢迎下载使用。








