


2022-2023学年山东省济宁市名校七下数学期末达标检测试题含答案
展开2022-2023学年山东省济宁市名校七下数学期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图所示,在直角坐标系内,原点O恰好是▱ABCD对角线的交点,若A点坐标为(2,3),则C点坐标为( )
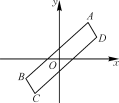
A.(-3,-2) B.(-2,3) C.(-2,-3) D.(2,-3)
2.菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( ) .
A.16 B.16![]() C.16
C.16![]() D.8
D.8![]()
3.在一次中学生田径运动会上,男子跳高项目的成绩统计如下:
成绩 |
|
|
|
|
|
人数 | 2 | 8 | 6 | 4 | 1 |
表中表示成绩的一组数据中,众数和中位数分别是![]()
![]()
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
4.不等式组![]() 的解集是x>4,那么m的取值范围是( )
的解集是x>4,那么m的取值范围是( )
A.m≤4 B.m<4 C.m≥4 D.m>4
5.如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
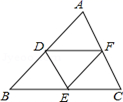
A.5 B.10 C.20 D.40
6.若关于![]() 的一元二次方程
的一元二次方程![]() 的一个根是1,则
的一个根是1,则![]() 的值为( )
的值为( )
A.-2 B.1 C.2 D.0
7.下列各式成立的是( )
A.![]() B.
B.![]() =3
=3
C.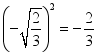 D.
D.![]() =3
=3
8.下列各式中,运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.直线![]() 与
与![]() 轴的交点坐标为( )
轴的交点坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]() ,则
,则![]() 的值为( )
的值为( )
A.9 B.-9 C.35 D.-35
二、填空题(本大题共有6小题,每小题3分,共18分)
11.菱形ABCD的两条对角线长分别为6和4,则菱形ABCD的面积是_____.
12.正方形的一边和一条对角线所成的角是________度.
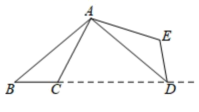
13.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则![]() 的大小为________.
的大小为________.
14.若点A(2,a)关于x轴的对称点是B(b,-3)则ab的值是 .
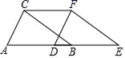
15.如图,将△ABC向右平移到△DEF位置,如果AE=8cm,BD=2cm,则△ABC移动的距离是___.
16.一组数据2,3,2,3,5的方差是__________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P.
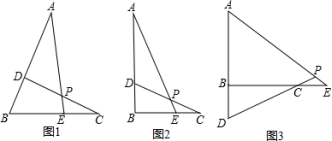
(1)点D、E分别在线段BA、BC上;
①若∠B=60°(如图1),且AD=BE,BD=CE,则∠APD的度数为 ;
②若∠B=90°(如图2),且AD=BC,BD=CE,求∠APD的度数;
(2)如图3,点D、E分别在线段AB、BC的延长线上,若∠B=90°,AD=BC,∠APD=45°,求证:BD=CE.
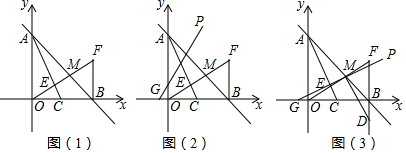
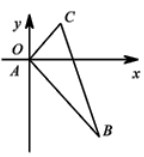
18.(8分)如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
(1)直接写出点F的坐标(用m表示);
(2)求证:OF⊥AC;
(3)如图(2),若m=2,点G的坐标为(-![]() ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
①求k的取值范围;
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.
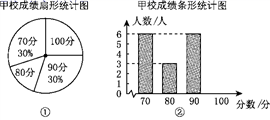
19.(8分)某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 |
|
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
20.(8分)阅读理解:
我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.
阅读下列材料,完成习题:
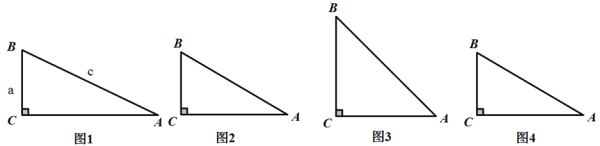
如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即sinA=![]()
例如:a=3,c=7,则sinA=![]()
问题:在Rt△ABC中,∠C=90°
(1)如图2,BC=5,AB=8,求sinA的值.
(2)如图3,当∠A=45°时,求sinB的值.
(3)AC=2![]() ,sinB=
,sinB=![]() ,求BC的长度.
,求BC的长度.
21.(8分)根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
22.(10分)如图,甲乙两船从港口A 同时出发,甲船以16海里/时的速度向南偏东 50°航行,乙船向北偏东 40°航行,3小时后,甲船到达B岛,乙船到达C岛,若C,B两岛相距60海里,问乙船的航速是多少?
23.(10分)某校检测学生跳绳水平,抽样调查了部分学生的“一分钟跳绳”成绩,并绘制了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
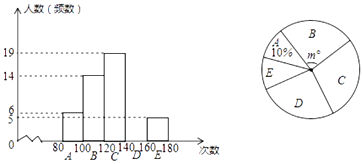
(1)抽样的人数是________人,补全频数分布直方图,扇形中![]() ________;
________;
(2)本次调查数据的中位数落在________组;
(3)如果“一分钟跳绳”成绩大于等于120次为优秀,那么该校2250名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
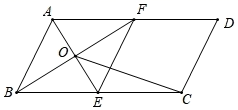
24.(12分)如图,在▱ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,∠ABC=60°,求OC的长.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、B
4、A
5、C
6、C
7、D
8、D
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、45
13、40°
14、1
15、3cm.
16、1.2
三、解下列各题(本大题共8小题,共72分)
17、(1)①60°;②45°;(2)见解析
18、(1)(m,![]() m)(2)见解析(3)①0<k<6②(
m)(2)见解析(3)①0<k<6②(![]() ,-
,-![]() )
)
19、 (1)54°;(2)补图见解析;(3)85分;(4)甲校20名同学的成绩相对乙校较整齐.
20、 (1)![]() ;(2)
;(2)![]() ;(3)2.
;(3)2.
21、(1)①x1=1,x2=1;②x1=1,x2=2;③x1=1,x2=1.(2)①x1=1,x2=2, ②x2-(1+n)x+n=3;(1)x1=1,x2=2.
22、乙船的速度是12海里/ 时.
23、(1)60,见解析,84;(2)C;(3)1500人
24、(1)证明见解析;(2)![]() .
.
西藏拉萨市名校2022-2023学年数学七下期末达标检测试题含答案: 这是一份西藏拉萨市名校2022-2023学年数学七下期末达标检测试题含答案,共8页。试卷主要包含了若,则代数式的值是,如图等内容,欢迎下载使用。
山东省烟台市名校2022-2023学年数学七下期末达标检测模拟试题含答案: 这是一份山东省烟台市名校2022-2023学年数学七下期末达标检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
山东省济宁市微山县2022-2023学年数学七下期末达标测试试题含答案: 这是一份山东省济宁市微山县2022-2023学年数学七下期末达标测试试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,.函数的自变量x的取值范围是等内容,欢迎下载使用。












