


2022-2023学年山东省泰安市泰前中学七年级数学第二学期期末经典模拟试题含答案
展开
这是一份2022-2023学年山东省泰安市泰前中学七年级数学第二学期期末经典模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,一元二次方程根的情况是,已知点等内容,欢迎下载使用。
2022-2023学年山东省泰安市泰前中学七年级数学第二学期期末经典模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列交通标志图案是轴对称图形的是( )A. B.
B. C.
C. D.
D. 2.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
2.如图所示,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )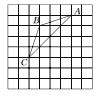 A.垂直 B.相等 C.平分 D.平分且垂直3.如图,在矩形ABCD中,
A.垂直 B.相等 C.平分 D.平分且垂直3.如图,在矩形ABCD中,![]() ,
,![]() ,将其折叠使AB落在对角线AC上,得到折痕AE,那么BE的长度为
,将其折叠使AB落在对角线AC上,得到折痕AE,那么BE的长度为![]()
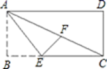 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.若直线y=ax+b的图象经过点(1,5),则关于
4.若直线y=ax+b的图象经过点(1,5),则关于![]() 的方程
的方程![]() 的解为( )A.
的解为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.在平面内,下列图案中,能通过图平移得到的是( )
5.在平面内,下列图案中,能通过图平移得到的是( )![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.如图,已知一次函数
6.如图,已知一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点(2,0),点(0,3).有下列结论:①关于
轴分别交于点(2,0),点(0,3).有下列结论:①关于![]() 的方程
的方程![]() 的解为
的解为![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() . 其中正确的是( )
. 其中正确的是( )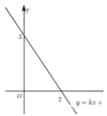 A.①② B.①③ C.②③ D.①③②7.一元二次方程
A.①② B.①③ C.②③ D.①③②7.一元二次方程![]() 根的情况是
根的情况是![]()
![]() A.有两个相等的实数根 B.有两个不相等的实数根C.没有实数根 D.不能确定8.在平行四边形ABCD中,∠A=55°,则∠D的度数是( )A.105° B.115° C.125° D.55°9.某机械厂七月份生产零件50万个,计划八、九月份共生产零件
A.有两个相等的实数根 B.有两个不相等的实数根C.没有实数根 D.不能确定8.在平行四边形ABCD中,∠A=55°,则∠D的度数是( )A.105° B.115° C.125° D.55°9.某机械厂七月份生产零件50万个,计划八、九月份共生产零件![]() 万个,设八、九月份平均每月的增长率为x,那么x满足的方程是
万个,设八、九月份平均每月的增长率为x,那么x满足的方程是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1,y2,y3的值的大小关系是( )A.y3<y1<y2 B.y1<y2<y3 C.y3>y1>y2 D.y1>y2>y311.若a>b,则下列各式中一定成立的是( )A.a+2<b+2 B.a-2<b-2 C.
10.已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1,y2,y3的值的大小关系是( )A.y3<y1<y2 B.y1<y2<y3 C.y3>y1>y2 D.y1>y2>y311.若a>b,则下列各式中一定成立的是( )A.a+2<b+2 B.a-2<b-2 C.![]() >
>![]() D.-2a>-2b12.下列给出的四个点中,在函数y=2x﹣3图象上的是( )A.(1,﹣1) B.(0,﹣2) C.(2,﹣1) D.(﹣1,6)二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在英文单词 believe 中,字母“e”出现的频率是_______.14.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.
D.-2a>-2b12.下列给出的四个点中,在函数y=2x﹣3图象上的是( )A.(1,﹣1) B.(0,﹣2) C.(2,﹣1) D.(﹣1,6)二、填空题(每题4分,满分20分,将答案填在答题纸上)13.在英文单词 believe 中,字母“e”出现的频率是_______.14.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2018BC和∠A2018CD的平分线交于点A2019,得∠A2019,则∠A2019=_____°.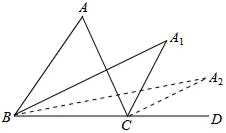 15.化简
15.化简![]() 的结果为________.16.如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.
的结果为________.16.如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是_____.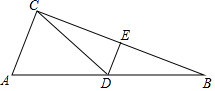 17.一组数据共有50个,分成四组后其中前三组的频率分别是0.25、0.15、0.3,则第四组数据的个数为______.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.(1)求S关于x的函数解析式;(2)当EFGH是正方形时,求S的值.
17.一组数据共有50个,分成四组后其中前三组的频率分别是0.25、0.15、0.3,则第四组数据的个数为______.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.(1)求S关于x的函数解析式;(2)当EFGH是正方形时,求S的值.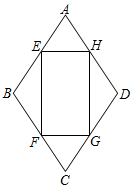 19.(5分)下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:(1)体育场离张强家的多远?张强从家到体育场用了多长时间?(2)体育场离文具店多远?(3)张强在文具店逗留了多久?(4)计算张强从文具店回家的平均速度.
19.(5分)下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:(1)体育场离张强家的多远?张强从家到体育场用了多长时间?(2)体育场离文具店多远?(3)张强在文具店逗留了多久?(4)计算张强从文具店回家的平均速度.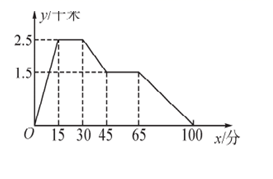 20.(8分)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,
20.(8分)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() ,
,![]() ,
,![]() ,
,![]() ,量得
,量得![]() .
.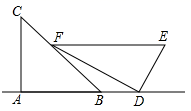 (1)试求点
(1)试求点![]() 到
到![]() 的距离.(2)试求
的距离.(2)试求![]() 的长. 21.(10分)某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
的长. 21.(10分)某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.![]() 根据图示填写下表: 平均数
根据图示填写下表: 平均数![]() 分中位数
分中位数![]() 分众数
分众数![]() 分A校______ 85______ B校85______ 100
分A校______ 85______ B校85______ 100![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.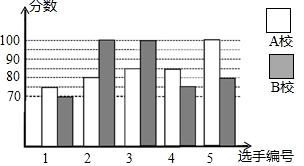 22.(10分)如图,在
22.(10分)如图,在![]() 中,点
中,点![]() 为边
为边![]() 的中点,点
的中点,点![]() 在
在![]() 内,
内,![]() 平分
平分![]() 点
点![]() 在
在![]() 上,
上,![]() .
.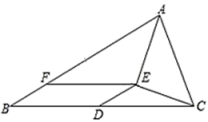 (1)求证:四边形
(1)求证:四边形![]() 是平行四边形;(2)线段
是平行四边形;(2)线段![]() 之间具有怎样的数量关系?证明你所得到的结论. 23.(12分)为贯彻落实关于“传承和弘扬中华优秀传统文化”的重要讲话精神,2018年5月27日我市举办了第二届湖南省青少年国学大赛永州复赛.本次比赛全市共有近200所学校4.6万名学生参加.经各校推荐报名、县区初赛选拔、市区淘汰赛的层层选拔,推选出优秀的学生参加全省的总决赛.下面是某县初赛时选手成绩的统计图表(部分信息未给出).
之间具有怎样的数量关系?证明你所得到的结论. 23.(12分)为贯彻落实关于“传承和弘扬中华优秀传统文化”的重要讲话精神,2018年5月27日我市举办了第二届湖南省青少年国学大赛永州复赛.本次比赛全市共有近200所学校4.6万名学生参加.经各校推荐报名、县区初赛选拔、市区淘汰赛的层层选拔,推选出优秀的学生参加全省的总决赛.下面是某县初赛时选手成绩的统计图表(部分信息未给出). 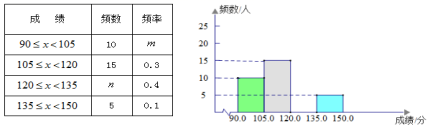 请根据图表信息回答下列问题:(1)在频数分布表中,
请根据图表信息回答下列问题:(1)在频数分布表中,![]() ,
,![]() .(2)请将频数直方图补充完整;(3)若测试成绩不低于120分为优秀,则本次测试的优秀率是多少? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、C4、C5、B6、A7、C8、C9、C10、D11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
.(2)请将频数直方图补充完整;(3)若测试成绩不低于120分为优秀,则本次测试的优秀率是多少? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、D3、C4、C5、B6、A7、C8、C9、C10、D11、C12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、
14、![]() 15、
15、![]() 16、117、2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)矩形EFGH的面积为S=-
16、117、2 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)矩形EFGH的面积为S=-![]() x2+
x2+![]() x(0<x<1);(2)S=
x(0<x<1);(2)S=![]() .19、(1)体育场离张强家2.5km,张强从家到体育场用了15min;(2)体育场离文具店1km;(3) 张强在文具店逗留了20min;(4)张强从文具店回家的平均速度为
.19、(1)体育场离张强家2.5km,张强从家到体育场用了15min;(2)体育场离文具店1km;(3) 张强在文具店逗留了20min;(4)张强从文具店回家的平均速度为![]() km/min20、(1)点
km/min20、(1)点![]() 与
与![]() 之间的距离为:
之间的距离为:![]() ;(2)
;(2)![]() .21、
.21、![]() ;85;1.(2)A校成绩好些.
;85;1.(2)A校成绩好些.![]()
![]() 校的方差
校的方差![]() ,B校的方差
,B校的方差![]() .A校代表队选手成绩较为稳定.22、(1)见详解;(2)
.A校代表队选手成绩较为稳定.22、(1)见详解;(2)![]() ,证明见详解.23、 (1)m=0.2,n=20;(2)图见解析;(3)50%.
,证明见详解.23、 (1)m=0.2,n=20;(2)图见解析;(3)50%.
相关试卷
这是一份2023-2024学年山东省泰安市泰前中学九上数学期末复习检测模拟试题含答案,共8页。
这是一份2023-2024学年山东省泰安市大津口中学九上数学期末经典模拟试题含答案,共8页。
这是一份2023-2024学年山东省泰安市泰前中学数学八年级第一学期期末综合测试试题含答案,共8页。试卷主要包含了某次知识竞赛共有20道题,规定,若,则的值为等内容,欢迎下载使用。









