


2022-2023学年山东省枣庄市薛城区数学七下期末统考模拟试题含答案
展开
这是一份2022-2023学年山东省枣庄市薛城区数学七下期末统考模拟试题含答案,共7页。试卷主要包含了下列计算中,正确的是等内容,欢迎下载使用。
2022-2023学年山东省枣庄市薛城区数学七下期末统考模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.下列选项中,矩形具有的性质是( )A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角2.五箱梨的质量(单位:千克)分别为:18,20,21,18,19,则这五箱梨质量的中位数和众数分是( )A.20和18 B.20和19 C.18和18 D.19和183.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF4.如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A.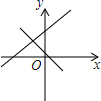 B.
B.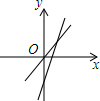 C.
C.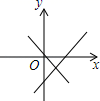 D.
D.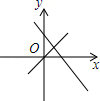 5.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有( )
5.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有( )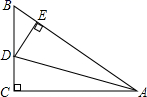 A.2个 B.3个 C.4个 D.1个6.关于x的方程x2-mx+2m=0的一个实数根是3,并且它的两个实数根恰好是等腰△ABC的两边长,则△ABC的腰长为( )A.3 B.6 C.6或9 D.3或67.如图,在正方形
A.2个 B.3个 C.4个 D.1个6.关于x的方程x2-mx+2m=0的一个实数根是3,并且它的两个实数根恰好是等腰△ABC的两边长,则△ABC的腰长为( )A.3 B.6 C.6或9 D.3或67.如图,在正方形![]() 中,
中,![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,且
边上,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )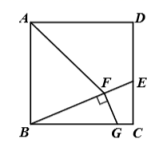 A.10 B.11 C.12 D.138.关于函数y=﹣x﹣2的图象,有如下说法:①图象过点(0,﹣2)②图象与x轴的交点是(﹣2,0)③由图象可知y随x的增大而增大 ④图象不经过第一象限 ⑤图象是与y=﹣x+2平行的直线,其中正确说法有( )A.5个 B.4个 C.3个 D.2个9.下列计算中,正确的是( )A.
A.10 B.11 C.12 D.138.关于函数y=﹣x﹣2的图象,有如下说法:①图象过点(0,﹣2)②图象与x轴的交点是(﹣2,0)③由图象可知y随x的增大而增大 ④图象不经过第一象限 ⑤图象是与y=﹣x+2平行的直线,其中正确说法有( )A.5个 B.4个 C.3个 D.2个9.下列计算中,正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )
10.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是24cm,那么△DEF的周长是( )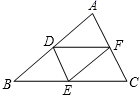 A.6cm B.12cm C.18cm D.48cm二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,矩形
A.6cm B.12cm C.18cm D.48cm二、填空题(本大题共有6小题,每小题3分,共18分)11.如图,矩形![]() 中,
中,![]() ,
,![]() ,将矩形沿
,将矩形沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处.则重叠部分
处.则重叠部分![]() 的面积为______.
的面积为______.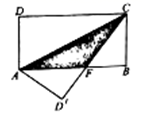 12.如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.
12.如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.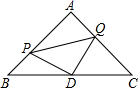 13.对分式
13.对分式![]() 和
和![]() 进行通分,它们的最简公分母是________.14.一组数据5,8,x,10,4的平均数是2x,则这组数据的中位数是___________.15.如图,在
进行通分,它们的最简公分母是________.14.一组数据5,8,x,10,4的平均数是2x,则这组数据的中位数是___________.15.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________. 16.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是___(填序号).
16.甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是___(填序号).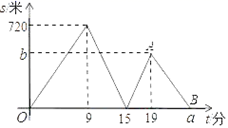 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() .(1)求证:
.(1)求证:![]() ;(2)若点
;(2)若点![]() 是
是![]() 的中点,
的中点,![]() ,求边
,求边![]() 的长.
的长.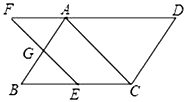 18.(8分)已知一次函数
18.(8分)已知一次函数![]() .(1)若这个函数的图象经过原点,求a的值.(2)若这个函数的图象经过一、三、四象限,求a的取值范围. 19.(8分)某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:视力频数(人)频率4.0≤x<4.3200.14.3≤x<4.6400.24.6≤x<4.9700.354.9≤x<5.2a0.35.2≤x<5.510b
.(1)若这个函数的图象经过原点,求a的值.(2)若这个函数的图象经过一、三、四象限,求a的取值范围. 19.(8分)某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:视力频数(人)频率4.0≤x<4.3200.14.3≤x<4.6400.24.6≤x<4.9700.354.9≤x<5.2a0.35.2≤x<5.510b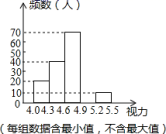 (1)本次调查的样本为 ,样本容量为 ;(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比. 20.(8分) “知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节项目的比赛,每人进行了4次测试,对照一定的标准,得分如下:甲:80,1,100,50;乙:75,80,75,1.如果你是教练,你打算安排谁代表学校参赛?请说明理由. 21.(8分)如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF。(1)若DE=DC,求证:四边形CDEF是菱形;(2)若AB=
(1)本次调查的样本为 ,样本容量为 ;(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比. 20.(8分) “知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节项目的比赛,每人进行了4次测试,对照一定的标准,得分如下:甲:80,1,100,50;乙:75,80,75,1.如果你是教练,你打算安排谁代表学校参赛?请说明理由. 21.(8分)如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF。(1)若DE=DC,求证:四边形CDEF是菱形;(2)若AB=![]() ,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。
,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。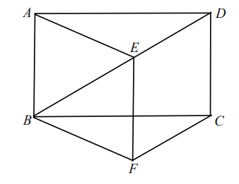 22.(10分) “金牛绿道行“活动需要租用
22.(10分) “金牛绿道行“活动需要租用![]() 、
、![]() 两种型号的展台,经前期市场调查发现,用
两种型号的展台,经前期市场调查发现,用![]() 元租用的
元租用的![]() 型展台的数量与用
型展台的数量与用![]() 元租用的
元租用的![]() 型展台的数量相同,且每个
型展台的数量相同,且每个![]() 型展台的价格比每个
型展台的价格比每个![]() 型展台的价格少
型展台的价格少![]() 元.(1)求每个
元.(1)求每个![]() 型展台、每个
型展台、每个![]() 型展台的租用价格分别为多少元(列方程解应用题);(2)现预计投入资金至多
型展台的租用价格分别为多少元(列方程解应用题);(2)现预计投入资金至多![]() 元,根据场地需求估计,
元,根据场地需求估计,![]() 型展台必须比
型展台必须比![]() 型展台多
型展台多![]() 个,问
个,问![]() 型展台最多可租用多少个. 23.(10分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.
型展台最多可租用多少个. 23.(10分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.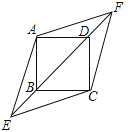 24.(12分)如图,直线
24.(12分)如图,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .(1)求
.(1)求![]() ,
,![]() 的值;(2)根据图像直接写出
的值;(2)根据图像直接写出![]() 时
时![]() 的取值范围;(3)垂直于
的取值范围;(3)垂直于![]() 轴的直线
轴的直线![]() 与直线
与直线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() ,若线段
,若线段![]() 长为2,求
长为2,求![]() 的值.
的值.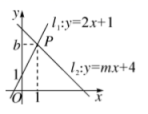 参考答案 一、选择题(每小题3分,共30分)1、C2、D3、B4、C5、B6、B7、D8、B9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1012、AB的中点.13、
参考答案 一、选择题(每小题3分,共30分)1、C2、D3、B4、C5、B6、B7、D8、B9、D10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、1012、AB的中点.13、![]() 14、515、30.16、①②③. 三、解下列各题(本大题共8小题,共72分)17、 (1)证明见解析;(2)AD=12.18、(1)
14、515、30.16、①②③. 三、解下列各题(本大题共8小题,共72分)17、 (1)证明见解析;(2)AD=12.18、(1)![]() ;(2)
;(2)![]() 19、(1)从中抽取的200名即将参加中考的初中毕业生的视力;200;(2)0.3;60;0.05,见解析;(3)70%.20、选乙代表学校参赛;理由见解析.21、(1)见解析;(2)
19、(1)从中抽取的200名即将参加中考的初中毕业生的视力;200;(2)0.3;60;0.05,见解析;(3)70%.20、选乙代表学校参赛;理由见解析.21、(1)见解析;(2)![]() 22、(1)每个A型展台,每个B型展台的租用价格分别为800元、1200元;(2)B型展台最多可租用31个.23、(1)证明见解析(2)菱形24、(1)
22、(1)每个A型展台,每个B型展台的租用价格分别为800元、1200元;(2)B型展台最多可租用31个.23、(1)证明见解析(2)菱形24、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
相关试卷
这是一份山东省枣庄市薛城区舜耕中学2022-2023学年七下数学期末教学质量检测试题含答案,共7页。试卷主要包含了如图,在中,,,则的度数是等内容,欢迎下载使用。
这是一份山东省枣庄市薛城区临城2022-2023学年七下数学期末联考模拟试题含答案,共7页。试卷主要包含了下列计算正确的是,估计的值在,计算的结果为等内容,欢迎下载使用。
这是一份山东省枣庄市薛城区奚仲中学2022-2023学年数学七下期末预测试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,如图,,,,则的度数为,在Rt△ABC中,∠C=90°,下列各式是最简二次根式的是等内容,欢迎下载使用。








