2022-2023学年山东省聊城市东阿县七年级数学第二学期期末调研试题含答案

这是一份2022-2023学年山东省聊城市东阿县七年级数学第二学期期末调研试题含答案，共7页。试卷主要包含了如果，下列各式中不正确的是，下列事件中，属于必然事件的是等内容，欢迎下载使用。
2022-2023学年山东省聊城市东阿县七年级数学第二学期期末调研试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．已知，则等于（　　）A． B． C．2 D．32．如图所示，点是的平分线上一点，于点，已知，则点到的距离是（    ）A．1.5 B．3C．5 D．63．在平面直角坐标系中，点关于x轴对称点所在的象限是A．第一象限 B．第二象限 C．第三象限 D．第四象限4．在学校举行的“阳光少年，励志青年”的演讲比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，则这组数据的众数是(    )A．95 B．90 C．85 D．805．某市招聘老师的笔试和面试的成绩均按百分制计，并且分别按40%和60%来计算综合成绩．王老师本次招聘考试的笔试成绩为90分，面试成绩为85分，经计算他的综合成绩是（  ）A．85分 B．87分 C．87.5分 D．90分6．如果，下列各式中不正确的是　　A． B． C． D．7．如图，有一直角三角形纸片ABC，∠C＝90°，∠B＝30°，将该直角三角形纸片沿DE折叠，使点B与点A重合，DE＝1，则BC的长度为(     )   A．2 B．＋2 C．3 D．28．下列事件中，属于必然事件的是A．如果都是实数，那么B．同时抛掷两枚质地均匀的骰子，向上一面的点数之和为13C．抛一枚质地均匀的硬币20次，有10次正面向上D．用长为4cm,4cm,9cm的三条线段围成一个等腰三角形9．一辆汽车以50的速度行驶,行驶的路程与行驶的时间之间的关系式为,其中变量是（           ）A．速度与路程 B．速度与时间 C．路程与时间 D．速度10．在某学校汉字听写大赛中，有21名同学参加比赛，预赛成绩各不相同，要取前10名才能参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需要再知道这21名同学成绩的(    )A．中位数 B．平均数 C．众数 D．方差二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，在矩形中，，，点为的中点，将沿折叠，使点落在矩形内点处，连接，则的长为________．12．端午节那天，“味美早餐店”的粽子打9折出售，小红的妈妈去该店买粽子花了54元钱，比平时多买了3个，则平时每个粽子卖_____元．13．若是正比例函数，则的值为______.14．方程的根是__________.15．如图，矩形中，，，是边上一点，连接，将沿翻折，点的对应点是，连接，当是直角三角形时，则的值是________16．小明用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每枝钢笔5元，那么小明最多能买________枝钢笔．三、解下列各题(本大题共8小题，共72分)17．（8分） “赏中华诗词，寻文化基因，品生活之美”某校举办了首届“中国诗词比赛”，全校师生同时默写50首古诗，每正确默写出一首古诗得2分，结果有600名学生进入决赛，从进入决赛的600名学生中随机抽取40名学生进行成绩分析，根据比赛成绩绘制出部分频数分布表和部分频数分布直方图如下列图表组别成绩x（分）频数（人数）第1组60≤x＜684第2组68≤x＜768第3组76≤x＜8412第4组84≤x＜92a第5组92≤x＜10010第3组12名学生的比赛成绩为：76、76、78、78、78、78、78、78、80、80、80、82请结合以上数据信息完成下列各题：（1）填空：a＝　   　所抽取的40名学生比赛成绩的中位数是　   　（2）请将频数分布直方图补充完整（3）若比赛成绩不低于84分的为优秀，估计进入决赛的学生中有多少名学生的比赛成绩为优秀？   18．（8分）（1）如图1，平行四边形纸片ABCD中，AD=5，S甲行四边形纸片ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′的位置，拼成四边形AEE′D，则四边形AEE′D的形状为　   　   A．平行四边形   B．菱形   C．矩形   D．正方形（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，剪下△AEF，将它平移至△DE′F′的位置，拼成四边形AFF′D．求证：四边形AFF′D是菱形．   19．（8分）如图，点C，D在线段AB上，△PCD是等边三角形，△ACP∽△PDB，（1）请你说明CD2=AC•BD；（2）求∠APB的度数．   20．（8分）某班进行了一次数学測验，将成绩绘制成频数分布表和频数直方图的一部分如下:成绩频数（人数）频率(1)在频数分布表中，的值为________，的值为________；(2)将频数直方图补充完整；(3)成绩在分以上(含)的学生人数占全班总人数的百分比是多少?   21．（8分）如图，△ABC与△CDE都是等边三角形，点E、F分别在AC、BC上，且EF∥AB（1）求证：四边形EFCD是菱形；（2）设CD＝2，求D、F两点间的距离．   22．（10分）如图，在平面直角坐标系中，一次函数图像经过点，且与轴相交于点，与正比例函数的图像相交于点，点的横坐标为.（1）求的值；（2）请直接写出不等式的解集.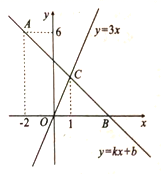   23．（10分）（1）如图1，观察函数y=|x|的图象，写出它的两条的性质；（2）在图1中，画出函数y=|x-3|的图象；根据图象判断：函数y=|x-3|的图象可以由y=|x|的图象向          平移          个单位得到；（3）①函数y=|2x+3|的图象可以由y=|2x|的图象向      平移           单位得到；②根据从特殊到一般的研究方法，函数y=|kx+3|（k为常数，k≠0）的图象可以由函数y=|kx|（k为常数，k≠0）的图象经过怎样的平移得到．   24．（12分）已知：如图，四边形ABCD中，∠B=90°,AB＝3，BC＝4，CD＝12，AD＝13，求四边形ABCD的面积?   参考答案 一、选择题(每小题3分,共30分)1、A2、B3、A4、B5、B6、B7、C8、A9、C10、A 二、填空题(本大题共有6小题，每小题3分，共18分)11、12、213、214、15、3或116、1 三、解下列各题(本大题共8小题，共72分)17、（1）6，78；（2）见解析；（3）240名18、（1）C；（2）详见解析.19、（1）见解析；（2）∠APB=120°．20、（1）10,0.1；（2）答案见解析；（3）占全班总人数百分比为.21、（1）见解析；（2）22、（1）；（2）23、（1）答案见解析；（2）画图见解析，右，3；（3）①左， ②答案见解析.24、36