


2022-2023学年广东省东莞市五校数学七年级第二学期期末监测试题含答案
展开这是一份2022-2023学年广东省东莞市五校数学七年级第二学期期末监测试题含答案,共7页。试卷主要包含了下列调查方法合适的是等内容,欢迎下载使用。
2022-2023学年广东省东莞市五校数学七年级第二学期期末监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.若![]() 在实数范围内有意义,则x的取值范围在数轴上表示正确的是( )
在实数范围内有意义,则x的取值范围在数轴上表示正确的是( )
A.![]()
![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
2.方程x2+2x﹣3=0的二次项系数、一次项系数、常数项分别是( )
A.1,2,3 B.1,2,﹣3 C.1,﹣2,3 D.﹣1,﹣2,3
3.一个多边形的内角和比其外角和的2倍多180°,那么这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.在一次编程比赛中,8位评委给参赛选手小李的打分如下:
9.0,9.0,9.1 ,10.0 ,9.0,9.1,9.0,9.1.
规定去掉一个最高分和一个最低分后的平均值做为选手的最后得分.小李的最后得分是( )
A.9.0 B.9.1 C.9.1 D.9.3
5.若分式![]() 有意义,则实数
有意义,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,在一次实践活动课上,小明为了测量池塘B、C两点间的距离,他先在池塘的一侧选定一点A,然后测量出AB、AC的中点D、E,且DE=10m,于是可以计算出池塘B、C两点间的距离是( )
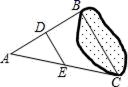
A.5m B.10m C.15m D.20m
7.下列调查方法合适的是( )
A.为了了解冰箱的使用寿命,采用普查的方式
B.为了了解全国中学生的视力状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式
8.木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )
A.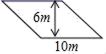 B.
B.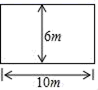 C.
C.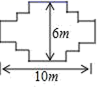 D.
D.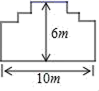
9.下列各式不能用平方差公式法分解因式的是( )
A.x2﹣4 B.﹣x2﹣y2 C.m2n2﹣1 D.a2﹣4b2
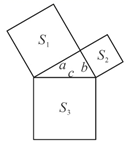
10.如图,已知直角三角形的三边长分别为a、b、c,以直角三角形的三边为边(或直径),分别向外作等边三角形、半圆、等腰直角三角形和正方形。那么,这四个图形中,其面积![]() 满足
满足![]() 的个数是( )
的个数是( )
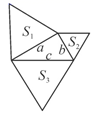
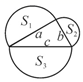
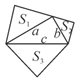
A.1 B.2 C.3 D.4
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,▱ABCD的对角线交于点O,且AB=5,△OCD的周长为16,则▱ABCD的两条对角线的和是______
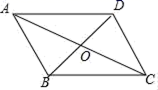
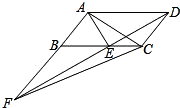
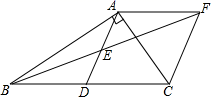
12.如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.
13.学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的___.
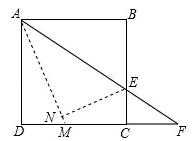
14.如图,正方形![]() 的边长为8,点
的边长为8,点![]() 是
是![]() 上的一点,连接
上的一点,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,
处,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,当
,当![]() 时,则
时,则![]() 的长为__.
的长为__.
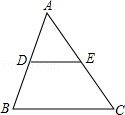
15.如图,△ABC中,D,E分别为AB,AC的中点,∠B=70°,则∠ADE= 度.
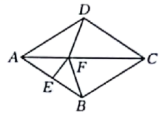
16.如图,在菱形![]() 中,
中,![]() ,
,![]() 的垂直平分线交对角线
的垂直平分线交对角线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ______.
______.
三、解下列各题(本大题共8小题,共72分)
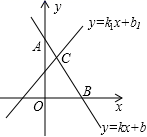
17.(8分)在数学学习中,及时对知识进行归纳和整理是提高学习效率的重要方法,善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
一次函数与方程(组)的关系:
(1)一次函数的解析式就是一个二元一次方程;
(2)点B的横坐标是方程kx+b=0的解;
(3)点C的坐标(x,y)中x,y的值是方程组①的解.
一次函数与不等式的关系:
(1)函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式kx+b>0的解集;
(2)函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式②的解集.
(一)请你根据以上归纳整理的内容在下面的数字序号后写出相应的结论:① ;② ;
(二)如果点B坐标为(2,0),C坐标为(1,3);
①直接写出kx+b≥k1x+b1的解集;
②求直线BC的函数解析式.
18.(8分)我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
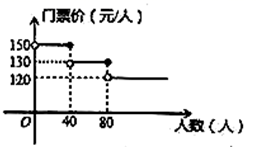
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变
的函数关系式,并写出自变![]() 的取值范围;
的取值范围;
(2)若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价![]() 元;人数超过80人时,每张门票降价
元;人数超过80人时,每张门票降价![]() 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求
元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求![]() 的值.
的值.
19.(8分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表
售价x(元) | 15 | 20 | 25 | ・・・・・・ |
日销售量y(件) | 25 | 20 | 15 | ・・・・・・ |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
20.(8分)如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.
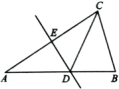
21.(8分)如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的垂直平分线.求证:
的垂直平分线.求证:![]() 是等腰三角形.
是等腰三角形.
22.(10分)某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
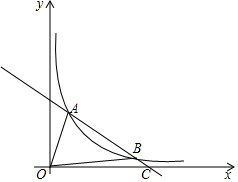
23.(10分)如图,一次函数y1=-![]() x+b的图象与反比例函数y2=
x+b的图象与反比例函数y2=![]() (x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为1.
(x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为1.
(1)在第一象限内,当x取何值时,y1>y2?(根据图直接写出结果)
(2)求反比例函数的解析式及△AOB的面积.
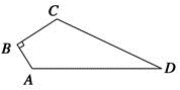
24.(12分)已知:如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、C
4、B
5、B
6、D
7、C
8、A
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、①②⑤
13、中位数.
14、![]()
15、1
16、![]() .
.
三、解下列各题(本大题共8小题,共72分)
17、(一)![]() ;kx+b<1;(二)①x≤1;②y=-3x+2
;kx+b<1;(二)①x≤1;②y=-3x+2
18、(1)当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() ;(2)甲、乙两团队联合购票比分别购票最多可节约1800元;(3)
;(2)甲、乙两团队联合购票比分别购票最多可节约1800元;(3)![]() 的值为15.
的值为15.
19、(1)一次函数解析式为y=-x+1;(2)每日所获利润为200元.
20、见解析
21、见解析
22、(1)4、5两个月销售量的平均增长率为20%;(2)每袋降价3元时,获利1920元.
23、 (1)1<x<1;(2)![]() ,面积为
,面积为![]() .
.
24、36
相关试卷
这是一份广东省东莞市五校联考2023-2024学年七年级上学期期末数学试题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省东莞市中学堂镇六校2022-2023学年数学七年级第二学期期末调研模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,若,则的值为,在相同时刻,物高与影长成正比等内容,欢迎下载使用。
这是一份广东省东莞市中学堂六校2022-2023学年七年级数学第二学期期末预测试题含答案,共7页。试卷主要包含了下列命题中的假命题是,若,则下列不等式一定成立的是.,下列计算中,正确的是等内容,欢迎下载使用。












