2022-2023学年山西省太原市志达中学七年级数学第二学期期末学业质量监测模拟试题含答案

2022-2023学年山西省太原市志达中学七年级数学第二学期期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．如图，平行四边形ABCD的对角线AC、BD相交于点O，已知AD=5，BD=8，AC=6，则△OBC的面积为（  ）

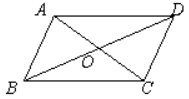
A．5 B．6 C．8 D．12

2．如图，过矩形的四个顶点作对角线、的平行线，分别相交于、、、四点，则四边形为（ ）

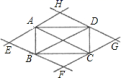
A．平行四边形 B．矩形 C．菱形 D．正方形

3．的值为（    ）

A． B． C．4 D．8

4．已知点A（﹣1，y1），点B（2，y2）在函数y＝﹣3x+2的图象上，那么y1与y2的大小关系是（　　）

A．y1＞y2 B．y1＜y2 C．y1＝y2 D．不能确定

5．若直角三角形的两条直角边的长分别为6和8，则斜边上的中线长是（  ）

A．6 B．5 C．7 D．不能确定

6．若一个多边形从一个顶点出发的对角线共有3条，则这个多边形的内角和为（   ）

A．360° B．540° C．720° D．1080°

7．如图，平行四边形的对角线交于点，且，的周长为25，则平行四边形的两条对角线的和是(    )

A．18 B．28 C．38 D．46

8．下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）

A． B． C． D．

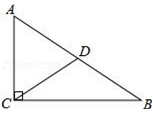
9．如图，在Rt△ABC中，AC＝6，BC＝8，D为斜边AB上一动点，DE⊥BC，DF⊥AC，垂足分别为E、F．则线段EF的最小值为（       ）

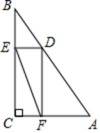
A．6 B． C．5 D．

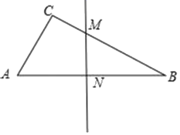
10．如图，Rt△ABC中，AB=9，BC=6，∠B=90˚，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（　　）

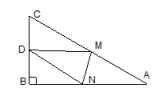
A．6 B．5 C．4 D．3

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，Rt△ABC中，∠ACB=90°，点D为斜边AB的中点，CD=6cm，则AB的长为      cm．

12．若+（y﹣2）2=0，那么（x+y）2018=_____．

13．方程x2＝2x的解是__________．

14．已知一次函数y=（-1-a2）x+1的图象过点（x1，2），（x2-1），则x1与x2的大小关系为______．

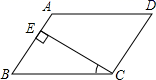
15．如图，在平行四边形ABCD中，CE⊥AB且E为垂足，如果∠A＝125°，则∠BCE＝____.

16．若最简二次根式和是同类二次根式，则m=_____．

三、解下列各题(本大题共8小题，共72分)

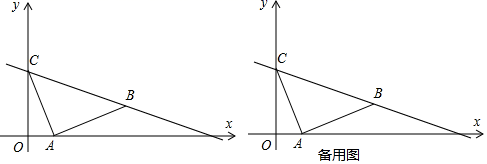
17．（8分）如图,已知平面直角坐标系中,、,现将线段绕点顺时针旋转得到点,连接.

(1)求出直线的解析式；

(2)若动点从点出发,沿线段以每分钟个单位的速度运动,过作交轴于,连接.设运动时间为分钟,当四边形为平行四边形时,求的值.

(3)为直线上一点,在坐标平面内是否存在一点,使得以、、、为顶点的四边形为菱形,若存在,求出此时的坐标；若不存在,请说明理由.

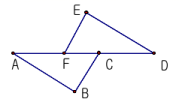
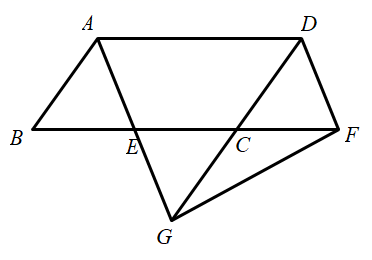
18．（8分）如图，已知 BC∥EF，BC=EF，AF=DC．试证明：AB=DE．

19．（8分）如图，四边形ABCD是平行四边形，E是BC边的中点，DF//AE，DF与BC的延长线交于点F，AE，DC的延长线交于点G，连接FG，若AD=3，AG=2，FG=，求直线AG与DF之间的距离．

20．（8分）对于实数a，b，定义运算“⊗”：a⊗b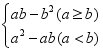＝，例如：5⊗3，因为5＞3，所以5⊗3＝5×3﹣32＝1．若x1，x2是一元二次方程x2﹣3x+2＝0的两个根，则x1⊗x2等于（　　）

A．﹣1 B．±2 C．1 D．±1

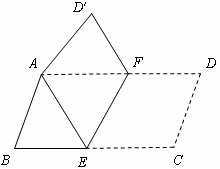
21．（8分）将平行四边形纸片按如图方式折叠，使点与重合，点落到处，折痕为．

（1）求证：；

（2）连结，判断四边形是什么特殊四边形？证明你的结论．

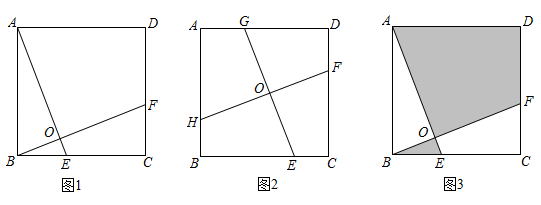
22．（10分）在正方形ABCD中．

（1）如图1，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，试判断AE与BF的数量关系，并说明理由；

（2）如图2，点E、F、G、H分别在边BC、CD、DA、AB上，EG、FH相交于点O，∠GOH=90°，且EG=7，求FH的长；

（3）如图3，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，若AB=5，图中阴影部分的面积与正方形的面积之比为4：5，求△ABO的周长．

23．（10分）如图，已知中，，的垂直平分线交于，交于，若，，求的长．

24．（12分）八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表

 (1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;

(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少，最少费用是多少元?

参考答案

一、选择题(每小题3分,共30分)

1、B

2、C

3、C

4、A

5、B

6、C

7、C

8、B

9、D

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1.

12、1

13、x1＝0， x2＝2

14、x1＜x1

15、1

16、1．

三、解下列各题(本大题共8小题，共72分)

17、（1）；（2）t=s时，四边形ABMN是平行四边形；（3）存在，点Q坐标为：或或或.

18、证明见解析

19、直线与之间的距离为

20、D

21、（1）证明见解析；（2）四边形AECF是菱形．证明见解析.

22、（1）AE=BF，理由见解析；（2）FH=7；（3）△AOB的周长为5+

23、

24、（1）y=-100x+3850；（2）当乙为2辆时，能保障费用最少，最少费用为3650元.