2022-2023学年山西省运城市夏县数学七年级第二学期期末质量检测试题含答案

这是一份2022-2023学年山西省运城市夏县数学七年级第二学期期末质量检测试题含答案，共6页。试卷主要包含了下列运算正确的是，若关于的方程有增根，则的值是等内容，欢迎下载使用。
2022-2023学年山西省运城市夏县数学七年级第二学期期末质量检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题(每小题3分,共30分)1．若的平均数是5，则的平均数是(     )A．5 B．6 C．7 D．82．介于两个相邻整数之间，这两个整数是(   )A．2和3 B．3和4 C．4和5 D．5和63．如表记录了甲、乙、丙、丁四名学生最近几次数学综合测试成绩的平均数与方差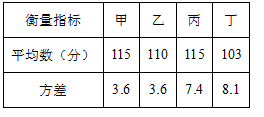：根据表中数据，要从中选择一名成好且发挥稳定的同学参加竟赛，应该选择（　　）A．甲 B．乙 C．丙 D．丁4．已知一次函数的图象经过第一、三、四象限，则下列结论正确的是（　）A． B．． C． D．5．下列运算正确的是(　　)A． B．2C．4×224 D．26．如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连接OE．若∠ADB＝30°，∠BAD＝100°，则∠BDC的度数是（　　）A．50° B．60° C．70° D．80°7．为了解某公司员工的年工资情况，小王随机调查了10位员工，某年工资(单位：万元)如下：3，3，3，4，5，5，6，6，8，20.下列统计量中，能合理反映该公司员工年工资水平的是(  )A．方差 B．众数 C．中位数 D．平均数8．下列所述图形中，既是中心对称图形，又是轴对称图形的是（ ）A．矩形 B．平行四边形 C．正五边形 D．正三角形9．若关于的方程有增根，则的值是（   ）A． B． C． D．10．关于反比例函数y＝的下列说法正确的是（   ）① 该函数的图象在第二、四象限；② A（x1、y1）、B（x2、y2）两点在该函数图象上，若x1＜x2，则y1＜y2；③ 当x＞2时，则y＞－2；④ 若反比例函数y＝与一次函数y＝x＋b的图象无交点，则b的范围是－4＜b＜4.A．① ③ B．①④ C．②③ D．②④二、填空题(本大题共有6小题，每小题3分，共18分)11．已知，则 ___________ .12．在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2，把△EFO放大，则点E的对应点E′的坐标是_____．13．颖颖同学用20元钱去买方便面35包，甲种方便面每包0.7元，乙种方便面每包0.5元，则她最多可买甲种方便面_____包．14．如图，在Rt△ABC中，BD平分∠ABC交AC于点D，过D作DE∥BC交AB于点E，若DE刚好平分∠ADB，且AE＝a，则BC＝_____．15．若x＋y＝1，xy＝-7，则x2y＋xy2＝_____________．16．数据6，5，7，7，9的众数是     ．三、解下列各题(本大题共8小题，共72分)17．（8分）（1）已知点A（2，0）在函数y=kx+3的图象上，求该函数的表达式并画出图形；（2）求该函数图象与坐标轴围成的三角形的面积.   18．（8分）如图，一次函数与反比例函数的图象交于A（1，4），B（4，n）两点．（1）求反比例函数和一次函数的解析式；（2）点P是x轴上的一动点，当PA+PB最小时，求点P的坐标；（3）观察图象，直接写出不等式的解集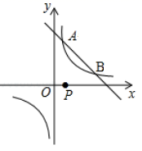．   19．（8分）在校园手工制作活动中，现有甲、乙两人接到手工制作纸花任务，已知甲每小时制作纸花比乙每小时制作纸花少20朵，甲制作120朵纸花的时间与乙制作160朵纸花的时间相同，求乙每小时制作多少朵纸花？   20．（8分）某体育用品商场采购员要到厂家批发购买篮球和排球共个,篮球个数不少于排球个数，付款总额不得超过元，已知两种球厂的批发价和商场的零售价如下表. 设该商场采购个篮球.品名厂家批发价/元/个商场零售价/元/个篮球排球（1）求该商场采购费用(单位:元)与(单位:个)的函数关系式,并写出自变最的取值范围：（2）该商场把这个球全都以零售价售出,求商场能获得的最大利润；（3）受原材料和工艺调整等因素影响,采购员实际采购时，低球的批发价上调了元/个，同时排球批发价下调了元/个.该体有用品商场决定不调整商场零售价，发现将个球全部卖出获得的最低利润是元,求的值.   21．（8分）感知：如图（1），已知正方形ABCD和等腰直角△EBF，点E在正方形BC边上，点F在AB边的延长线上，∠EBF=90°，连结AE、CF．易证：∠AEB=∠CFB（不需要证明）．探究：如图（2），已知正方形ABCD和等腰直角△EBF，点E在正方形ABCD内部，点F在正方形ABCD外部，∠EBF=90°，连结AE、CF．求证：∠AEB=∠CFB应用：如图（3），在（2）的条件下，当A、E、F三点共线时，连结CE，若AE=1，EF=2，则CE=______．   22．（10分）如图，矩形ABCD中，AB＝4，BC＝3，以BD为腰作等腰△BDE交DC的延长线于点E，求BE的长．   23．（10分）我市晶泰星公司安排名工人生产甲、乙两种产品，每人每天生产件甲产品或件乙产品.根据市场行情测得，甲产品每件可获利元，乙产品每件可获利元.而实际生产中，生产乙产品需要数外支出一定的费用，经过核算，每生产件乙产品，当天每件乙产品平均荻利减少元，设每天安排人生产乙产品.(1)根据信息填表：产品种类每天工人数(人)每天产量(件)每件产品可获利润(元)甲  乙  (2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多元，试问：该企业每天生产甲、乙产品可获得总利润是多少元?   24．（12分）在等腰三角形ABD 中， ABAD．(I)试利用无刻度的直尺和圆规作图，求作：点C ，使得四边形 ABCD 是菱形.(保留作图痕迹，不写作法和证明)；(II)在菱形 ABCD 中，连结 AC 交 BD 于点O，若 AC8，BD6，求AB边上的高h的长.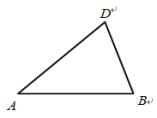   参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、B5、C6、A7、C8、A9、A10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、12、（-8，4）或（8，-4）13、114、6a15、﹣716、1． 三、解下列各题(本大题共8小题，共72分)17、（1） ，画图形见解析；（2）18、（1）反比例函数的解析式为；一次函数的解析式为y=-x+5；（2）点P的坐标为（，0）；（3）x＜0或1≤x≤419、乙每小时制作80朵纸花．20、（1），；（2）商场能获得的最大利润为元；（3）的值为.21、感知：见解析；探究：见解析；应用： ．22、.23、 (1) ；；；(2)该企业每天生产甲、乙产品可获得总利润是元.24、 (I)见解析；(II)