


2022-2023学年广东省佛山市名校数学七年级第二学期期末统考试题含答案
展开2022-2023学年广东省佛山市名校数学七年级第二学期期末统考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.下列调查中,适宜采用抽样调查方式的是( )
A.调查八年级某班学生的视力情况
B.调查乘坐飞机的旅客是否携带违禁物品
C.调查某品牌LED灯的使用寿命
D.学校在给学生订制校服前尺寸大小的调查
2.八年级某同学6次数学小测验的成绩分别为95分,80分,85分,95分,95分,85分,则该同学这6次成绩的众数和中位数分别是( )
A.95分,95分 B.95分,90分 C.90分,95分 D.95分,85分
3.把![]() 根号外的因式移入根号内,结果( )
根号外的因式移入根号内,结果( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图像是( )
A.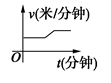 B.
B.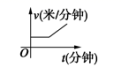
C.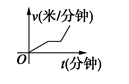 D.
D.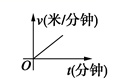
5.若正比例函数的图象经过点(![]() ,2),则这个图象必经过点( ).
,2),则这个图象必经过点( ).
A.(1,2) B.(![]() ,
,![]() ) C.(2,
) C.(2,![]() ) D.(1,
) D.(1,![]() )
)
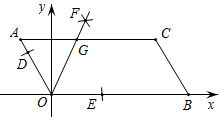
6.如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A.(![]() ﹣1,2) B.(
﹣1,2) B.(![]() ,2) C.(3﹣
,2) C.(3﹣![]() ,2) D.(
,2) D.(![]() ﹣2,2)
﹣2,2)
7.一次函数y=kx+b(k<0,b>0)的图象可能是( )
A.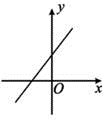
![]() B.
B.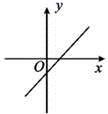 C.
C.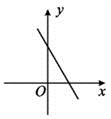
![]() D.
D.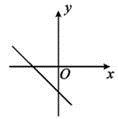
8.估计![]() 的值在( )
的值在( )
A.2到3之间 B.3到4之间 C.4到5之间 D.5到6之间
9.若点 ![]() ,
,![]() 都在反比例函数
都在反比例函数 ![]() 的图象上,则
的图象上,则![]() 与
与![]() 的大小关系是
的大小关系是 ![]()
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
10. “已知:正比例函数 ![]() 与反比例函数
与反比例函数 ![]() 图象相交于
图象相交于 ![]() 两点, 其横坐标分别是 1 和﹣1,求不等式
两点, 其横坐标分别是 1 和﹣1,求不等式 ![]() 的解集.”对于这道题,某同学是这样解答的:“由图象可知:当
的解集.”对于这道题,某同学是这样解答的:“由图象可知:当![]() 或
或![]() 时,
时,![]() ,所以不等式
,所以不等式![]() 的解集是
的解集是![]() 或
或![]() ”.他这种解决问题的思路体现的数学思想方法是( )
”.他这种解决问题的思路体现的数学思想方法是( )
A.数形结合 B.转化 C.类比 D.分类讨论
二、填空题(本大题共有6小题,每小题3分,共18分)
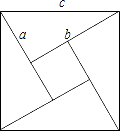
11.2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.
12.外角和与内角和相等的平面多边形是_______________.
13.化简:![]() +
+![]() =___.
=___.
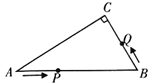
14.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点P是边AB上的一个动点,以每秒3个单位的速度按照从
,若点P是边AB上的一个动点,以每秒3个单位的速度按照从![]() 运动,同时点Q从
运动,同时点Q从![]() 以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若
以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动。在运动过程中,设运动时间为t,若![]() 为直角三角形,则t的值为________.
为直角三角形,则t的值为________.
15.一个多边形的内角和与外角和的比是4:1,则它的边数是 .
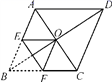
16.如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
三、解下列各题(本大题共8小题,共72分)
17.(8分)计算:﹣22﹣|2﹣![]() |+(﹣1)2017×(π﹣3)0﹣(
|+(﹣1)2017×(π﹣3)0﹣(![]() )﹣1
)﹣1
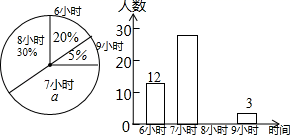
18.(8分)为了了解某校初中各年级学生每天的平均睡眠时间(单位:![]() ,精确到
,精确到![]() ,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_____,所抽查的学生人数为______.
的值为_____,所抽查的学生人数为______.
(2)求出平均睡眠时间为8小时的人数,并补全条形统计图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1800名,请你估计睡眠不足(少于8小时)的学生数.
19.(8分)关于x的一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
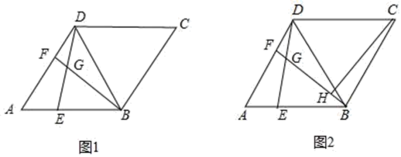
20.(8分)菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.
(1)如图1,求∠BGD的度数;
(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;
(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
21.(8分)在平面直角坐标系,直线y=2x+2交x轴于A,交y轴于 D,
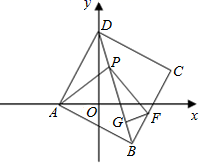
(1)直接写直线y=2x+2与坐标轴所围成的图形的面积
(2)以AD为边作正方形ABCD,连接AD,P是线段BD上(不与B,D重合)的一点,在BD上截取PG=![]() ,过G作GF垂直BD,交BC于F,连接AP.
,过G作GF垂直BD,交BC于F,连接AP.
问:AP与PF有怎样的数量关系和位置关系?并说明理由;
(3)在(2)中的正方形中,若∠PAG=45°,试判断线段PD,PG,BG之间有何关系,并说明理由.
22.(10分)如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程![]() 、
、![]() 与时间
与时间![]() 的关系,观察图象并回答下列问题:
的关系,观察图象并回答下列问题:
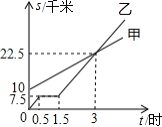
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙有事耽搁,停下来时间为 小时;
(3)甲从出发起,经过 小时与乙相遇;
(4)甲行走的平均速度是多少千米![]() 小时?
小时?
23.(10分)已知关于x的一元二次方程x2﹣(n+3)x+3n=1.求证:此方程总有两个实数根.
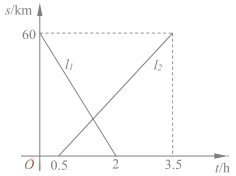
24.(12分)A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h.
(2)甲出发后多少时间两人恰好相距5km?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、A
5、D
6、A
7、C
8、B
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、四边形
13、1
14、![]() 或
或![]() 或
或![]()
15、1.
16、2
三、解下列各题(本大题共8小题,共72分)
17、![]()
18、(1)45%,60人;(2)18人,条形统计图见解析;(3)众数7,平均数7.2;(4)1170人.
19、 (1) ![]() ;(2)
;(2) ![]() .
.
20、(1)∠BGD=120°;(2)见解析;(3)S四边形ABCD=26![]() .
.
21、(1)1;(1)AP=PF且AP⊥PF,理由见解析;(3)PD1+BG1=PG1,理由见解析
22、(1)1;(2)1;(3)3;(4)![]()
23、见解析.
24、(1)![]() ; 30; 20;(2)甲出发后1.3h或者1.5h时,甲乙相距5km.
; 30; 20;(2)甲出发后1.3h或者1.5h时,甲乙相距5km.
广东省佛山市名校2023-2024学年九上数学期末监测模拟试题含答案: 这是一份广东省佛山市名校2023-2024学年九上数学期末监测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,若关于x的方程,若,则的值为,已知y=等内容,欢迎下载使用。
广东省揭阳市名校2022-2023学年数学七年级第二学期期末统考试题含答案: 这是一份广东省揭阳市名校2022-2023学年数学七年级第二学期期末统考试题含答案,共6页。试卷主要包含了下列命题的逆命题能成立的有等内容,欢迎下载使用。
广东省中山市名校2022-2023学年七年级数学第二学期期末统考试题含答案: 这是一份广东省中山市名校2022-2023学年七年级数学第二学期期末统考试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列各命题的逆命题成立的是,要使分式有意义,则x应满足等内容,欢迎下载使用。












