

2022-2023学年广东省惠州市惠阳高级中学七年级数学第二学期期末监测试题含答案
展开
这是一份2022-2023学年广东省惠州市惠阳高级中学七年级数学第二学期期末监测试题含答案,共8页。试卷主要包含了某电信公司有A、B两种计费方案等内容,欢迎下载使用。
2022-2023学年广东省惠州市惠阳高级中学七年级数学第二学期期末监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.函数![]() 与
与![]() 在同一平面直角坐标系中的大致图像是( )A.
在同一平面直角坐标系中的大致图像是( )A.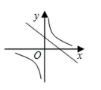 B.
B.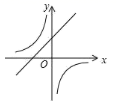 C.
C.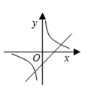 D.
D. 2.如图,矩形
2.如图,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴上、顶点
轴正半轴上、顶点![]() 在
在![]() 轴正半轴上,反比例函数
轴正半轴上,反比例函数![]() 的图象分别与
的图象分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )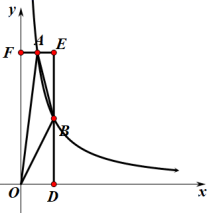 A.2 B.4 C.6 D.83.如果把分式
A.2 B.4 C.6 D.83.如果把分式![]() 中的
中的![]() 和
和![]() 都扩大3倍,那么分式的值()A.扩大3倍 B.缩小3倍C.缩小6倍 D.不变4.某电信公司有A、B两种计费方案:月通话费用y(元)与通话时间x(分钟)的关系,如图所示,下列说法中正确的是( )
都扩大3倍,那么分式的值()A.扩大3倍 B.缩小3倍C.缩小6倍 D.不变4.某电信公司有A、B两种计费方案:月通话费用y(元)与通话时间x(分钟)的关系,如图所示,下列说法中正确的是( )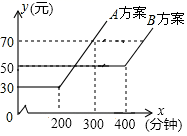 A.月通话时间低于200分钟选B方案划算B.月通话时间超过300分钟且少于400分钟选A方案划算C.月通话费用为70元时,A方案比B方案的通话时间长D.月通话时间在400分钟内,B方案通话费用始终是50元5.若菱形的周长为16,高为2,则菱形两个邻角的比为( )A.6:1 B.5:1 C.4:1 D.3:16.已知空气单位体积质量是
A.月通话时间低于200分钟选B方案划算B.月通话时间超过300分钟且少于400分钟选A方案划算C.月通话费用为70元时,A方案比B方案的通话时间长D.月通话时间在400分钟内,B方案通话费用始终是50元5.若菱形的周长为16,高为2,则菱形两个邻角的比为( )A.6:1 B.5:1 C.4:1 D.3:16.已知空气单位体积质量是![]() ,将
,将![]() 用科学记数法表示为( )A.
用科学记数法表示为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.已知x=1是一元二次方程
7.已知x=1是一元二次方程![]() 的解,则b的值为( )A.0 B.1 C.
的解,则b的值为( )A.0 B.1 C.![]() D.28.在Rt△ABC中,BC是斜边,∠B=40°,则∠C=( )A.90° B.60° C.50° D.40°9.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作
D.28.在Rt△ABC中,BC是斜边,∠B=40°,则∠C=( )A.90° B.60° C.50° D.40°9.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作![]() 交BC的延长线于点F,连结
交BC的延长线于点F,连结![]() 若
若![]() ,则EF的值为
,则EF的值为![]()
![]()
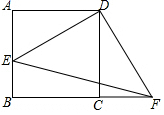 A.3 B.
A.3 B.![]() C.
C.![]() D.410.如图,点
D.410.如图,点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在双曲线
在双曲线![]() 上,且
上,且![]() 轴,
轴,![]() 、
、![]() 在
在![]() 轴上,若四边形
轴上,若四边形![]() 为矩形,则它的面积为( )
为矩形,则它的面积为( )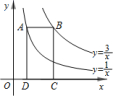 A.1 B.2 C.3 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.在平面直角坐标系
A.1 B.2 C.3 D.4二、填空题(本大题共有6小题,每小题3分,共18分)11.在平面直角坐标系![]() 中,
中,![]() 中,点
中,点![]() ,若随
,若随![]() 变化的一族平行直线
变化的一族平行直线![]() 与
与![]() (包括边界)相交,则
(包括边界)相交,则![]() 的取值范围是______.
的取值范围是______.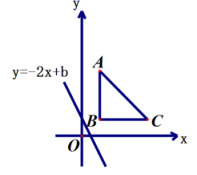 12.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:班级参加人数中位数方差平均数甲55149191135乙55151110135某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是______.(填序号)13.将直线y=﹣2x+4向下平移5个单位长度,平移后直线的解析式为_____.14.对于实数x,我们[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,[﹣2.5]=﹣3,若[
12.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:班级参加人数中位数方差平均数甲55149191135乙55151110135某同学根据上表分析得出如下结论:(l)甲、乙两班学生成绩的平均水平相同;(2)乙班优秀(每分钟输入汉字超过150个为优秀)的人数多于甲班优秀的人数;(3)甲班的成绩波动比乙班的成绩波动小、上述结论中正确的是______.(填序号)13.将直线y=﹣2x+4向下平移5个单位长度,平移后直线的解析式为_____.14.对于实数x,我们[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,[﹣2.5]=﹣3,若[![]() ]=5,则x的取值范围是______.15.如图,矩形
]=5,则x的取值范围是______.15.如图,矩形![]() 中,
中,![]() 是
是![]() 上一点(不与
上一点(不与![]() 重合),点
重合),点![]() 在边
在边![]() 上运动,
上运动,![]() 分别是
分别是![]() 的中点,线段
的中点,线段![]() 长度的最大值是__________.
长度的最大值是__________.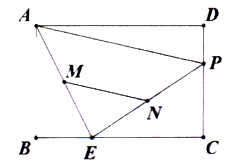 16.我们把“宽与长的比等于黄金比的矩形称为黄金矩形”,矩形
16.我们把“宽与长的比等于黄金比的矩形称为黄金矩形”,矩形![]() 是黄金矩形,且
是黄金矩形,且![]() ,则
,则![]() __________.三、解下列各题(本大题共8小题,共72分)17.(8分)某服装制造厂要在开学前赶制3000套服装,为了尽快完成任务,厂领导合理调配,加强第一线人力,使每天完成的校服比原计划多了20%,结果提前4天完成任务.问原计划每天能完成多少套校服? 18.(8分)(1)计算:(-1)2019-|-4|+(3.14-π)0+(
__________.三、解下列各题(本大题共8小题,共72分)17.(8分)某服装制造厂要在开学前赶制3000套服装,为了尽快完成任务,厂领导合理调配,加强第一线人力,使每天完成的校服比原计划多了20%,结果提前4天完成任务.问原计划每天能完成多少套校服? 18.(8分)(1)计算:(-1)2019-|-4|+(3.14-π)0+(![]() )-1(2)先化简,再求值:(1-
)-1(2)先化简,再求值:(1-![]() )÷
)÷![]() ,再从-1,0,1和2中选一个你认为合适的数作为x的值代入求值. 19.(8分)为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.
,再从-1,0,1和2中选一个你认为合适的数作为x的值代入求值. 19.(8分)为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.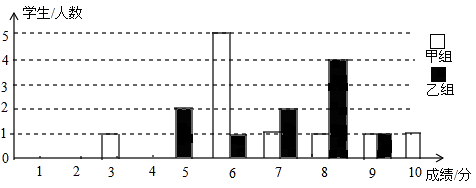 (1)补充完成下面的成绩统计分析表:组别
(1)补充完成下面的成绩统计分析表:组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由. 20.(8分)如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值;(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值;(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.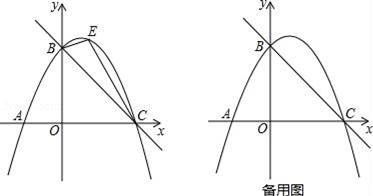 21.(8分)如图,在等腰
21.(8分)如图,在等腰![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 重合),连结
重合),连结![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.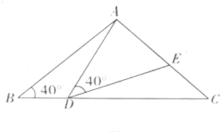 (1)当
(1)当![]() 时,
时,![]() = °;点
= °;点![]() 从点
从点![]() 向点
向点![]() 运动时,
运动时,![]() 逐渐变 (填“大”或“小”);(2)当
逐渐变 (填“大”或“小”);(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;(3)在点
,请说明理由;(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形. 22.(10分)已知△ABC的三条边长分别为2,5,6,在△ABC所在平面内画一条直线,将△ABC分成两个三角形,使其中一个三角形为等腰三角形.
是等腰三角形. 22.(10分)已知△ABC的三条边长分别为2,5,6,在△ABC所在平面内画一条直线,将△ABC分成两个三角形,使其中一个三角形为等腰三角形.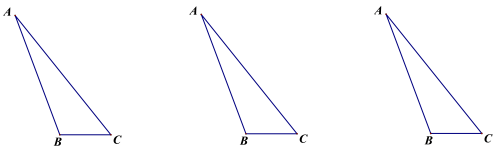 (1)这样的直线最多可以画 条;(2)请在三个备用图中分别画出符合条件的一条直线,要求每个图中得到的等腰三角形腰长不同,尺规作图,不写作法,保留作图痕迹. 23.(10分)如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:
(1)这样的直线最多可以画 条;(2)请在三个备用图中分别画出符合条件的一条直线,要求每个图中得到的等腰三角形腰长不同,尺规作图,不写作法,保留作图痕迹. 23.(10分)如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题: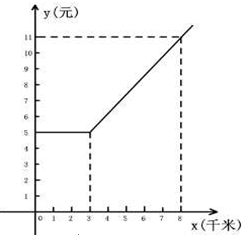 (1)当行使8千米时,收费应为 元;(2)从图象上你能获得哪些信息?(请写出2条)① ________②____________________________(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式. 24.(12分) (1)计算:
(1)当行使8千米时,收费应为 元;(2)从图象上你能获得哪些信息?(请写出2条)① ________②____________________________(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式. 24.(12分) (1)计算:![]() ;(2)解方程:
;(2)解方程:![]() . 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、D4、D5、B6、C7、C8、C9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、
. 参考答案 一、选择题(每小题3分,共30分)1、A2、D3、D4、D5、B6、C7、C8、C9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、(1),(2).13、y=-2x-1.14、46≤x<115、516、
12、(1),(2).13、y=-2x-1.14、46≤x<115、516、![]() 或
或![]() 三、解下列各题(本大题共8小题,共72分)17、原计划每天能完成125套.18、(1)-1;(2)x=-1时,原式=
三、解下列各题(本大题共8小题,共72分)17、原计划每天能完成125套.18、(1)-1;(2)x=-1时,原式=![]() .19、(1)6;7.1;(2)甲;(3)乙组的平均分,中位数高于甲组,方差小于甲组,故乙组成绩好于甲组20、(1)
.19、(1)6;7.1;(2)甲;(3)乙组的平均分,中位数高于甲组,方差小于甲组,故乙组成绩好于甲组20、(1)![]() ;(2)点E的坐标是(2,1)时,△BEC的面积最大,最大面积是1;(1)P的坐标是(﹣1,
;(2)点E的坐标是(2,1)时,△BEC的面积最大,最大面积是1;(1)P的坐标是(﹣1,![]() )、(5,
)、(5,![]() )、(﹣1,
)、(﹣1,![]() ).21、(1)35°,小;(2)当DC=3时,△ABD≌△DCE,理由见解析;(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.22、(1)7;(2)见解析23、(1)11;(2)如:出租车起步价(3千米内)为5元;超出3千米,每千米加收1.2元等;(3)
).21、(1)35°,小;(2)当DC=3时,△ABD≌△DCE,理由见解析;(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.22、(1)7;(2)见解析23、(1)11;(2)如:出租车起步价(3千米内)为5元;超出3千米,每千米加收1.2元等;(3)![]() .24、 (1)
.24、 (1)![]() ;(2)
;(2)![]() ,
,![]()
相关试卷
这是一份2023-2024学年广东省惠州市惠阳高级中学七年级(上)期末数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省惠州市惠阳区2023-2024学年九年级数学第一学期期末监测模拟试题含答案,共7页。试卷主要包含了函数中,自变量的取值范围是等内容,欢迎下载使用。
这是一份2023-2024学年广东省惠州市惠阳高级中学数学九上期末调研模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。








