2022-2023学年广西桂林市全州县七年级数学第二学期期末学业质量监测模拟试题含答案

2022-2023学年广西桂林市全州县七年级数学第二学期期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．施工队要铺设米的下水管道,因在中考期间需停工天,每天要比原计划多施工米才能按时完成任务.设原计划每天施工米,所列方程正确的是(   )

A． B．

C． D．

2．下列说法正确的是（  　）

A．两锐角分别相等的两个直角三角形全等

B．两条直角边分别相等的两直角三角形全等

C．一个命题是真命题，它的逆命题一定也是真命题

D．经过旋转，对应线段平行且相等

3．刘翔在出征北京奥运会前刻苦进行110米跨栏训练，教练对他20次的训练成绩进行统计分析，判断他的成绩是否稳定，则教练需要知道刘翔这20次成绩的（　　）

A．众数 B．平均数 C．频数 D．方差

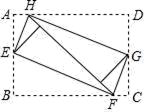
4．如图，将矩形ABCD的四个角向内折叠铺平，恰好拼成一个无缝隙无重叠的矩形EFGH，若EH＝5，EF＝12，则矩形ABCD的面积是（    ） 

A．13                                       B．                                        C．60                                       D．120

5．化简的结果为(　　)

A．﹣ B．﹣y C． D．

6．一个五边形的内角和为（　　）

A．540°    B．450°    C．360°    D．180°

7．菱形的对角线长分别为6和8，则该菱形的面积是（    ）

A．24 B．48 C．12 D．10

8．若＝﹣a，则a的取值范围是（　　）

A．﹣3≤a≤0 B．a≤0 C．a＜0 D．a≥﹣3

9．若关于的不等式组有三个整数解，且关于的分式方程有整数解，则满足条件的所有整数的和是（   ）

A． B． C． D．

10．要判断甲、乙两队舞蹈队的身高哪队比较整齐，通常需要比较这两队舞蹈队身高的（　　）

A．方差 B．中位数 C．众数 D．平均数

11．对于函数y=﹣2x+2，下列结论：①当x＞1时，y＜0；②它的图象经过第一、二、四象限；③它的图象必经过点（﹣1，2）；④y的值随x的增大而增大，其中正确结论的个数是（　　）

A．1    B．2    C．3    D．4

12．如果分式有意义，那么的取值范围是（    ）

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．若，则的值为__________，的值为________.

14．已知，则代数式的值为_____．

15．因式分解：　   　．

16．将直线向上平移3个单位长度与直线重合，则直线的解析式为__________．

17．把一元二次方程2x2﹣x﹣1＝0用配方法配成a（x﹣h）2+k＝0的形式（a，h，k均为常数），则h和k的值分别为_____

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

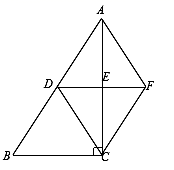
18．（5分）如图，在Rt△ABC中，∠ACB＝90°，D、E分别是AB、AC的中点，连接DE并延长至点F，使EF＝DE，连接AF，DC．求证：四边形ADCF是菱形．

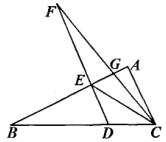
19．（5分）如图，△ABC 的面积为 63，D 是 BC 上的一点，且 BD：BC＝2：3， DE∥AC 交 AB 于点 E，延长 DE 到 F，使 FE：ED＝2：1．连结 CF 交 AB 点于 G．

(1)求△BDE 的面积；

(2)求 的值；

 (3)求△ACG 的面积．

20．（8分）甲、乙两个筑路队共同承担一段一级路的施工任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用15天．且甲队单独施工60天和乙队单独施工40天的工作量相同．

（1）甲、乙两队单独完成此项任务各需多少天？

（2）若甲、乙两队共同工作了4天后，乙队因设备检修停止施工，由甲队单独继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？

21．（10分）几何学的产生，源于人们对土地面积测量的需要，以面积早就成为人们认识图形性质与几何证明的有效工具，可以说几何学从一开始便与面积结下了不解之缘．我们已经掌握了平行四边形面积的求法，但是一般四边形的面积往往不易求得，那么我们能否将其转化为平行四边形来求呢？

（1）方法1：如图①，连接四边形的对角线，，分别过四边形的四个顶点作对角线的平行线，所作四条线相交形成四边形，易证四边形是平行四边形．请直接写出S四边形ABCD和之间的关系：_______________．

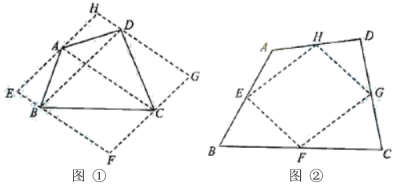
方法2：如图②，取四边形四边的中点，，，，连接，，，，

（2）求证：四边形是平行四边形；

（3）请直接写出S四边形ABCD与之间的关系：_____________．

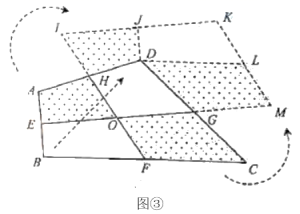
方法3：如图③，取四边形四边的中点，，，，连接，交于点．先将四边形绕点旋转得到四边形，易得点，，在同一直线上；再将四边形绕点旋转得到四边形，易得点，，在同一直线上；最后将四边形沿方向平移，使点与点重合，得到四边形；

（4）由旋转、平移可得_________，_________，所以，所以点，，在同一直线上，同理，点，，也在同一点线上，所以我们拼接成的图形是一个四边形．

（5）求证：四边形是平行四边形．

（注意：请考生在下面2题中任选一题作答如果多做，则按所做的第一题计分）

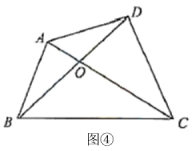
（6）应用1：如图④，在四边形中，对角线与交于点，，，，则S四边形ABCD=            ．

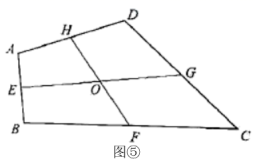
（7）应用2：如图⑤，在四边形中，点，，，分别是，，，的中点，连接，交于点，，，，则S四边形ABCD=___________

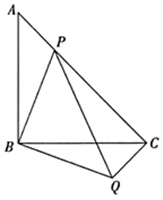
22．（10分）如图，等腰直角中，，点在上，将绕顶点沿顺时针方向旋转90°后得到.

（1）求的度数；

（2）当，时，求的大小；

（3）当点在线段上运动时（不与，重合），求证：.

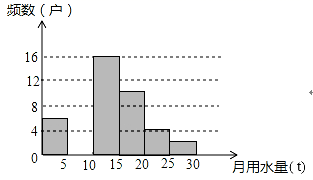
23．（12分）八年级（1）班同学为了解某小区家庭月均用水情况，随机调査了该小区部分家庭，并将调查数据整理成如下两幅不完整的统计图表：

请根据以上信息，解答以下问题：

（1）直接写出频数分布表中的m、n的值并把频数直方图补充完整；

（2）求出该班调查的家庭总户数是多少？

（3）求该小区用水量不超过15的家庭的频率．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、B

3、D

4、D

5、D

6、A

7、A

8、A

9、B

10、A

11、B

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、  ，

14、3

15、．

16、

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、证明见解析.

19、（1）△BDE的面积是28；（2）；（3）9

20、（1）甲队单独完成此项任务需15天，乙队单独完成此项任务需30天；（2）1天

21、（1）S四边形ABCD；（2）见详解；（1）S四边形ABCD ；（4）AEO，OEB；（5）见详解；（6）；（7）

22、（1）；（1）；（3）见解析.

23、（1）m=12,n=0.08;（2）50；（3）0.68.