2022-2023学年德州陵城区五校联考七下数学期末检测试题含答案

这是一份2022-2023学年德州陵城区五校联考七下数学期末检测试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，点关于原点对称点的坐标是等内容，欢迎下载使用。
2022-2023学年德州陵城区五校联考七下数学期末检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．已知一组数据2，3，4，x，1，4，3有唯一的众数4，则这组数据的中位数是(   )A．2 B．3 C．4 D．52．下列各式中，能用公式法分解因式的是（    ）①；      ②；      ③；    ④；     ⑤A．2个 B．3个 C．4个 D．5个3．一个不透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是(　　)A．至少有1个球是红球 B．至少有1个球是白球C．至少有2个球是红球 D．至少有2个球是白球4．下列命题：①一组对边平行且另一组对边相等的四边形是平行四边形；②一组邻角相等的平行四边形是矩形；③顺次连结矩形四边中点得到的四边形是菱形；④如果一个菱形的对角线相等，那么它一定是正方形．其中真命题个数是（    ）A．个 B．个 C．个 D．个5．如图，直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有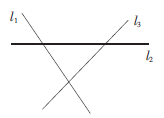（    ）A．一处 B．二处 C．三处 D．四处6．如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，连接DE，EF，DF，则下列说法不正确的是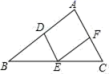（　　）A．S△DEF＝S△ABCB．△DEF≌△FAD≌△EDB≌△CFEC．四边形ADEF，四边形DBEF，四边形DECF都是平行四边形D．四边形ADEF的周长＝四边形DBEF的周长＝四边形DECF的周长7．某型号的汽车在路面上的制动距离s＝，其中变量是（      ）A． s   v2  B．s C．v D． s  v8．点关于原点对称点的坐标是（    ）A． B． C． D．9．如果一个三角形三条边的长分别是7，24，25，则这个三角形的最大内角的度数是（　　）A．30° B．45° C．60° D．90°10．如图，已知点P是∠AOB平分线上的一点，∠AOB=60°，PD⊥OA ，M是OP的中点，DM=4 cm．若点C是OB上一个动点，则PC的最小值为（ 　）cm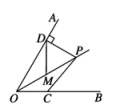．A．7 B．6 C．5 D．4二、填空题(本大题共有6小题，每小题3分，共18分)11．已知关于的方程会产生增根，则的值为________．12．已知菱形ABCD的对角线长度是8和6，则菱形的面积为_____．13．已知反比例函数的图象与一次函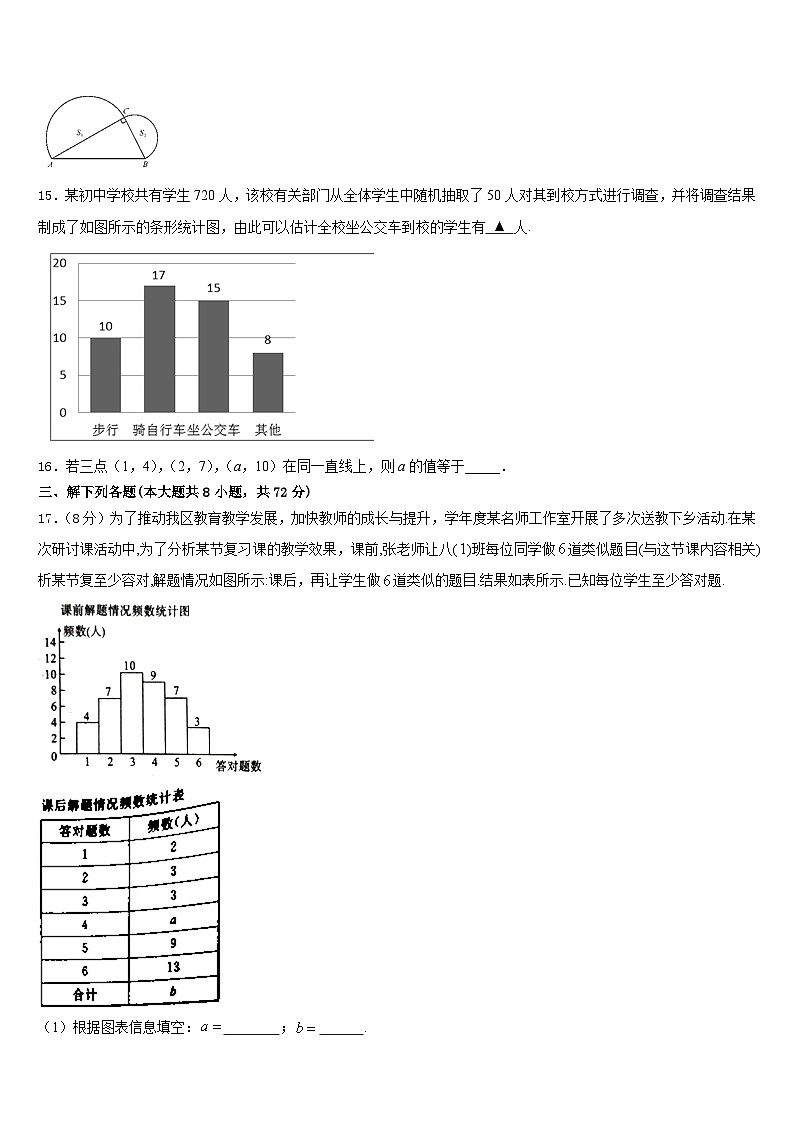数y＝k（x﹣3）+2（k＞0）的图象在第一象限交于点P，则点P的横坐标a的取值范围为___．14．如图，已知在Rt△ABC中，∠ACB＝90°，AB＝4，分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1＋S2等_________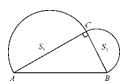．15．某初中学校共有学生720人，该校有关部门从全体学生中随机抽取了50人对其到校方式进行调查，并将调查结果制成了如图所示的条形统计图，由此可以估计全校坐公交车到校的学生有 ▲ 人.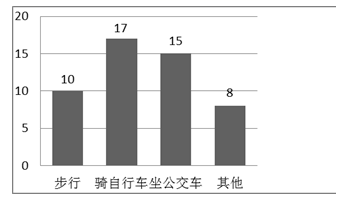16．若三点（1，4），（2，7），（a，10）在同一直线上，则a的值等于_____．三、解下列各题(本大题共8小题，共72分)17．（8分）为了推动我区教育教学发展，加快教师的成长与提升，学年度某名师工作室开展了多次送教下乡活动.在某次研讨课活动中,为了分析某节复习课的教学效果，课前,张老师让八()班每位同学做道类似题目(与这节课内容相关)析某节复至少容对,解题情况如图所示:课后，再让学生做道类似的题目.结果如表所示.已知每位学生至少答对题.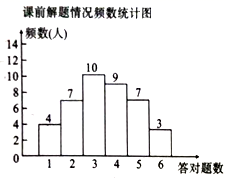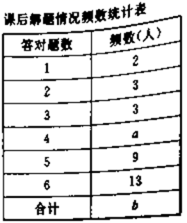（1）根据图表信息填空：          ；        .（2）该班课前解题时答对题数的众数是        ；课后答对题数的中位数是        .（3）通过计算课前，课后学生答对题数的平均数，评价这节复习课的教学效果.   18．（8分）某市米厂接到加工大米任务，要求天内加工完大米.米厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止，设甲、乙两车间各自加工大米数量与甲车间加工时间(天)之间的关系如图1所示；未加工大米与甲车间加工时间(天)之间的关系如图2所示，请结合图像回答下列问题 (1)甲车间每天加工大米__________；=______________；(2)直接写出乙车间维修设备后，乙车间加工大米数量与(天)之间的函数关系式，并指出自变量的取值范围.   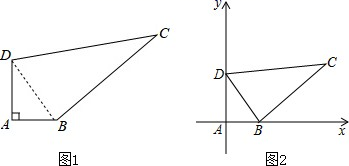19．（8分）如图所示，四边形 ABCD，∠A=90°，AB=3m，BC=12m，CD=13m，DA=4m．(1)求证：BD⊥CB；(2)求四边形 ABCD 的面积；(3)如图 2，以 A 为坐标原点，以 AB、AD所在直线为 x轴、y轴建立直角坐标系，点P在y轴上，若 S△PBD=S四边形ABCD，求 P的坐标．   20．（8分）如图，在△ABC中，∠C＝90°，∠A＝30°，边AB的垂直平分线交AB于点D，交AC于点E．求证：AE＝2CE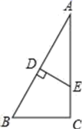．   21．（8分）在正方形中，平分交边于点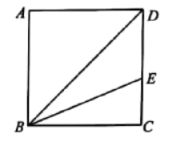．（1）尺规作图：过点作于；（保留作图痕迹，不写作法）（2）在（1）的条件下，连接，求的度数．   22．（10分）（1）|﹣3|+2sin45°﹣+（﹣）﹣1（2）（）÷   23．（10分）近年来，随着我国科学技术的迅猛发展，很多行业已经由“中国制造”升级为“中国创造”，高铁事业是“中国创造”的典范，甲、乙两个城市的火车站相距1280千米，加开高铁后，从甲站到乙站的运行时间缩短了11个小时，大大方便了人们出行，已知高铁行驶速度是原来火车速度的3.2倍，求高铁的行驶速度．   24．（12分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4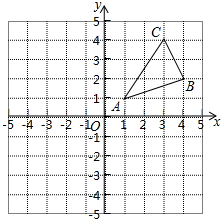）.（1）请画出△ABC向左平移5个单位长度后得到的△ABC；（2）请画出△ABC关于原点对称的△ABC；   参考答案 一、选择题(每小题3分,共30分)1、B2、B3、B4、B5、D6、D7、D8、A9、D10、D 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、113、2＜a＜1．14、15、21616、1． 三、解下列各题(本大题共8小题，共72分)17、（1）；；（2）题，题；（3）这节复习课的教学效果明显.，18、解：(1)；； (2)，19、（1）证明见解析；（1）36m1；（3）P 的坐标为（0，-1）或（0，10）．20、见解析21、（1）作图见解析；（2）67.5°．22、（1）-1（2）23、高铁的行驶速度为1千米/时．24、