


2022-2023学年江苏省东海晶都双语学校数学七下期末检测模拟试题含答案
展开2022-2023学年江苏省东海晶都双语学校数学七下期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.若![]() ,则下列变形错误的是( )
,则下列变形错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
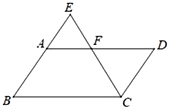
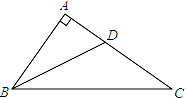
2.如图,在![]() 中,
中,![]() 是边
是边![]() 上的一点,射线
上的一点,射线![]() 和
和![]() 的延长线交于点
的延长线交于点![]() ,如果
,如果![]() ,那么
,那么![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若x>y,则下列式子错误的是( )
A.x﹣3>y﹣3 B.﹣3x>﹣3y C.x+3>y+3 D.![]()
4.下列调查的样本所选取方式,最具有代表性的是( )
A.在青少年中调查年度最受欢迎的男歌手
B.为了解班上学生的睡眠时间,调查班上学号为双号的学生的睡眠时间
C.为了解你所在学校的学生每天的上网时间,对八年级的同学进行调查
D.对某市的出租车司机进行体检,以此反映该市市民的健康状况
5.某校八![]() 班
班![]() 名同学在
名同学在![]() 分钟投篮测试中的成绩如下:
分钟投篮测试中的成绩如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:个),则这组数据的中位数、众数分别是( )
,(单位:个),则这组数据的中位数、众数分别是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
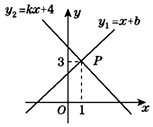
6.如图,一次函数![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列四个二次根式中,是最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若函数![]() 的图象与坐标轴有三个交点,则b的取值范围是
的图象与坐标轴有三个交点,则b的取值范围是![]()
![]()
A.![]() 且
且![]() B.
B.![]() C.
C.![]() D.
D.![]()
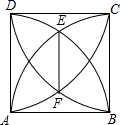
9.如图,已知正方形 ABCD 的边长为 1,以顶点 A、B 为圆心,1 为半径的两弧交于点 E, 以顶点 C、D 为圆心,1 为半径的两弧交于点 F,则 EF 的长为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若点P(a,b)在第二象限内,则a,b的取值范围是( )
A.a<0,b>0 B.a>0,b>0 C.a>0,b<0 D.a<0,b<0
二、填空题(本大题共有6小题,每小题3分,共18分)
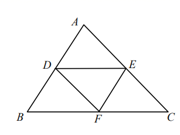
11.如图,在△ABC中,AB=5,AC=6,BC=7,点D、E、F分别是边AB、AC、BC的中点,连接DE、DF、EF,则△DEF的周长是_____________。
12.当x=________时,分式![]() 的值为0
的值为0
13.在▱ABCD中,∠BAD的平分线AE把边BC分成5和6两部分,则▱ABCD的周长为_____.
14.一组数据3,4,6,8,x的中位数是x,且x是满足不等式组![]() 的整数,则这组数据的平均数是 .
的整数,则这组数据的平均数是 .
15.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是_____.
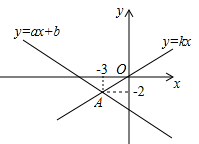
16.如图,函数![]() 和
和![]() 的图象交于点
的图象交于点![]() ,根据图象可知,关于
,根据图象可知,关于![]() 的不等式
的不等式![]() 的解集为________.
的解集为________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE,DF.
(1)试判断四边形AEDF的形状,并证明你的结论;
(2)若∠BAC=60°,AE=6,求四边形AEDF的面积;
(3)△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.
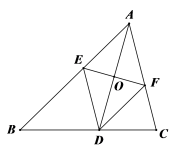
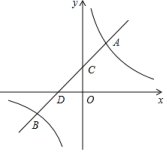
18.(8分)如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
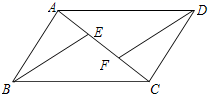
19.(8分)如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
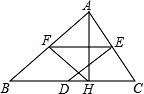
20.(8分)在△ABC中,AH⊥BC于H,D、E、F分别是BC、CA、AB的中点.求证:DE=HF.
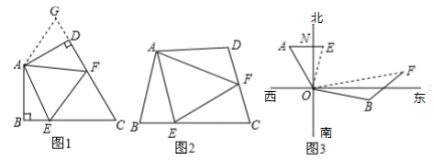
21.(8分)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120∘ ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点.且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系. 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离.
22.(10分)某校学生在“蓝天下的至爱”帮困活动中,纷纷拿零花钱,参加募捐活动.甲班学生共募捐840元,乙班学生共募捐1000元,乙班学生的数比甲班学生的人均捐款数多5元,且人数比甲班少2名,求甲班和乙班学生的人数.
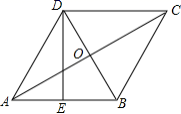
23.(10分)如图,菱形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() .
.
(1)求对角线![]() ,
,![]() 的长;
的长;
(2)求菱形![]() 的面积.
的面积.
24.(12分)《九章算术》“勾股”章的问题::“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙各行几何?”大意是说:如图,甲乙二人从A处同时出发,甲的速度与乙的速度之比为7:3,乙一直向东走,甲先向南走十步到达C处,后沿北偏东某方向走了一段距离后与乙在B处相遇,这时,甲乙各走了多远?
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、B
4、B
5、D
6、D
7、D
8、A
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、9
12、1
13、32或1
14、1.
15、1
16、x>−1
三、解下列各题(本大题共8小题,共72分)
17、(1)四边形AEDF是菱形,证明见详解;(2)![]() ;(3)在△ABC中,当∠BAC=90°时,四边形AEDF是正方形.
;(3)在△ABC中,当∠BAC=90°时,四边形AEDF是正方形.
18、(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)(12,
;(3)(12,![]() )或(-12,
)或(-12,![]() )
)
19、BE∥DF,BE=DF,理由见解析
20、证明见解析.
21、问题背景:EF=BE+DF,理由见解析;探索延伸:结论仍然成立,理由见解析;实际应用:210海里.
22、甲班学生的人数为42名,乙班学生的人数为40名.
23、(1)![]() ,
,![]() ;(2)
;(2)![]()
24、甲行24.1步,乙行10.1步.
江苏省东海晶都双语学校2023-2024学年九上数学期末学业水平测试试题含答案: 这是一份江苏省东海晶都双语学校2023-2024学年九上数学期末学业水平测试试题含答案,共7页。试卷主要包含了把二次函数配方后得等内容,欢迎下载使用。
江苏省东海晶都双语学校2023-2024学年九上数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省东海晶都双语学校2023-2024学年九上数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了如图,下列命题是真命题的个数是等内容,欢迎下载使用。
江苏省东海晶都双语学校2023-2024学年数学八年级第一学期期末质量跟踪监视试题含答案: 这是一份江苏省东海晶都双语学校2023-2024学年数学八年级第一学期期末质量跟踪监视试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。












