


2022-2023学年江苏省南京六中学数学七下期末检测模拟试题含答案
展开
这是一份2022-2023学年江苏省南京六中学数学七下期末检测模拟试题含答案,共7页。
2022-2023学年江苏省南京六中学数学七下期末检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )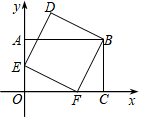 A.(1,2.5) B.(1,1+
A.(1,2.5) B.(1,1+ ![]() ) C.(1,3) D.(
) C.(1,3) D.(![]() ﹣1,1+
﹣1,1+ ![]() )2.如图,图中的小正方形的边长为1,到点A的距离为
)2.如图,图中的小正方形的边长为1,到点A的距离为![]() 的格点的个数是( )
的格点的个数是( )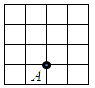 A.7 B.6 C.5 D.43.下列四组线段中,不能组成直角三角形的是( )A.
A.7 B.6 C.5 D.43.下列四组线段中,不能组成直角三角形的是( )A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() C.
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]() 4.若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A.
4.若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )A.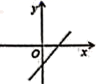 B.
B.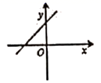 C.
C.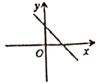 D.
D.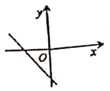 5.如果把分式
5.如果把分式![]() 中的x和y都扩大3倍,那么分式的值( )A.不变 B.扩大3倍 C.缩小3倍 D.无法确定6.如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )
中的x和y都扩大3倍,那么分式的值( )A.不变 B.扩大3倍 C.缩小3倍 D.无法确定6.如图,在矩形ABCD中,对角线AC、BD交与点O,以下说法错误的是( )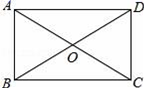 A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD7.如图,直线
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD7.如图,直线![]() 过点
过点![]() 和点
和点![]() ,则方程
,则方程![]() 的解是( )
的解是( )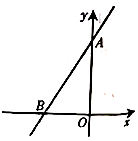 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A.2cm B.4cm C.6cm D.8cm9.下列图形中,不是中心对称图形的是( )A.
8.已知直角三角形中30°角所对的直角边为2cm,则斜边的长为( )A.2cm B.4cm C.6cm D.8cm9.下列图形中,不是中心对称图形的是( )A.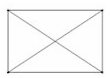 B.
B.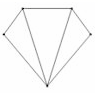 C.
C.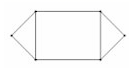 D.
D.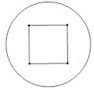 10.某校为了了解学生在校午餐所需的时间,抽查了 20 名同学在校午餐所需的时间,获得如 下数据(单位:分):10,12,15,10,1,18,19,18,20,34,22,25,20,18,18,20,15,1,21,1.若将这些数据分为 5组,则组距是( )A.4 分 B.5 分 C.6 分 D.7 分二、填空题(本大题共有6小题,每小题3分,共18分)11.甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1000米,甲超出乙150米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点还有_____米.
10.某校为了了解学生在校午餐所需的时间,抽查了 20 名同学在校午餐所需的时间,获得如 下数据(单位:分):10,12,15,10,1,18,19,18,20,34,22,25,20,18,18,20,15,1,21,1.若将这些数据分为 5组,则组距是( )A.4 分 B.5 分 C.6 分 D.7 分二、填空题(本大题共有6小题,每小题3分,共18分)11.甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1000米,甲超出乙150米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点还有_____米.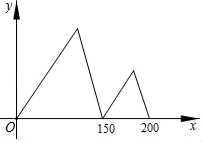 12.如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
12.如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.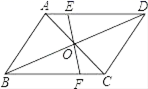 13.如图,将直角三角形纸片
13.如图,将直角三角形纸片![]() 置于平面直角坐标系中,已知点
置于平面直角坐标系中,已知点![]() ,将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图
,将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图![]() 位置,第二次旋转至图
位置,第二次旋转至图![]() 位置,···,则直角三角形纸片旋转
位置,···,则直角三角形纸片旋转![]() 次后,其直角顶点与坐标轴原点的距离为__________.
次后,其直角顶点与坐标轴原点的距离为__________. 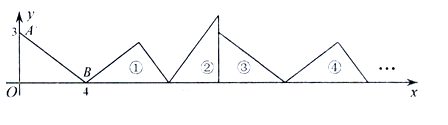 14.若y=
14.若y=![]() ,则x+y= .15.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2
,则x+y= .15.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2![]() ,那么△DEF的周长是_____.
,那么△DEF的周长是_____.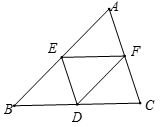 16.在平面直角坐标系中有两点
16.在平面直角坐标系中有两点![]() 和点
和点![]() .则这两点之间的距离是________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,四边形ABCD为矩形,C点在
.则这两点之间的距离是________.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,四边形ABCD为矩形,C点在![]() 轴上,A点在
轴上,A点在![]() 轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).(1)求G点坐标(2)求直线EF解析式(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由
轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).(1)求G点坐标(2)求直线EF解析式(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由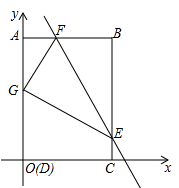 18.(8分)已知关于x的一元二次方程3x2﹣6x+1﹣k=0有实数根,k为负整数.(1)求k的值;(2)如果这个方程有两个整数根,求出它的根. 19.(8分)计算:(1)
18.(8分)已知关于x的一元二次方程3x2﹣6x+1﹣k=0有实数根,k为负整数.(1)求k的值;(2)如果这个方程有两个整数根,求出它的根. 19.(8分)计算:(1)![]() ×
×![]() .(2)
.(2)![]() . 20.(8分)如图所示,已知一次函数的图像直线AB经过点(0,6)和点(-2,0).
. 20.(8分)如图所示,已知一次函数的图像直线AB经过点(0,6)和点(-2,0).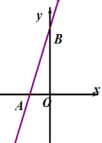 (1)求这个函数的解析式;(2)直线AB与x轴交于点A,与y轴交于点B,求△AOB的面积. 21.(8分)某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:(1)求出图象中②部分的解析式,并求出完成此项工程共需的天数;(2)该工程共支付8万元,若按完成的工作量所占比例支付工资,甲工程队应得多少元?
(1)求这个函数的解析式;(2)直线AB与x轴交于点A,与y轴交于点B,求△AOB的面积. 21.(8分)某项工程由甲、乙两个工程队合作完成,先由甲队单独做3天,剩下的工作由甲、乙两工程队合作完成,工程进度满足如图所示的函数关系:(1)求出图象中②部分的解析式,并求出完成此项工程共需的天数;(2)该工程共支付8万元,若按完成的工作量所占比例支付工资,甲工程队应得多少元?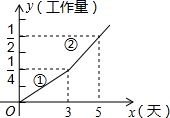 22.(10分) “2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式(2)求小林跑步的速度,以及图2中a的值(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?
22.(10分) “2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式(2)求小林跑步的速度,以及图2中a的值(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?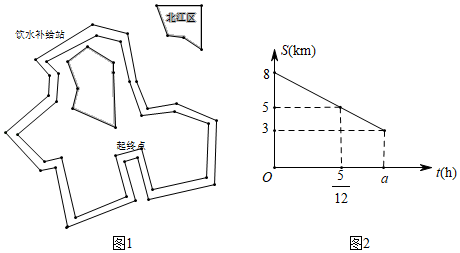 23.(10分)甲、乙、丙三支排球队共同参加一届比赛,由抽签决定其中两队先打一场,然后胜者再和第三队(第一场轮空者)比赛,争夺冠军.(1)如果采用在暗盒中放形状大小完全一致的两黑一白三个小球,摸到白色小球的第一场轮空直接晋级进入决赛,那么甲队摸到白色小球的概率是多少?(2)如果采用三队各抛一枚硬币,当出现二正一反或二反一正时则由抛出同面的两个队先打一场,而出现三枚同面(同为正面或反面)时,则重新抛,试用“树形图”或表格表示第一轮抽签(抛币)所有可能的结果,并指出必须进行第二轮抽签的概率. 24.(12分)如图所示,有一长方形的空地,长为
23.(10分)甲、乙、丙三支排球队共同参加一届比赛,由抽签决定其中两队先打一场,然后胜者再和第三队(第一场轮空者)比赛,争夺冠军.(1)如果采用在暗盒中放形状大小完全一致的两黑一白三个小球,摸到白色小球的第一场轮空直接晋级进入决赛,那么甲队摸到白色小球的概率是多少?(2)如果采用三队各抛一枚硬币,当出现二正一反或二反一正时则由抛出同面的两个队先打一场,而出现三枚同面(同为正面或反面)时,则重新抛,试用“树形图”或表格表示第一轮抽签(抛币)所有可能的结果,并指出必须进行第二轮抽签的概率. 24.(12分)如图所示,有一长方形的空地,长为![]() 米,宽为
米,宽为![]() 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.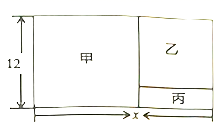
![]() 请用含
请用含![]() 的代数式表示正方形乙的边长; ;
的代数式表示正方形乙的边长; ;![]() 若丙地的面积为
若丙地的面积为![]() 平方米,请求出
平方米,请求出![]() 的值. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、A5、A6、D7、B8、B9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、5012、113、
的值. 参考答案 一、选择题(每小题3分,共30分)1、C2、B3、A4、A5、A6、D7、B8、B9、B10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、5012、113、![]() 14、1.15、10+
14、1.15、10+![]() 16、
16、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)G(0,4-
三、解下列各题(本大题共8小题,共72分)17、(1)G(0,4-![]() );(2)
);(2)![]() ;(3)
;(3)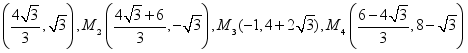 .18、(2)k=﹣2,﹣2.(2)方程的根为x2=x2=2.19、(1)
.18、(2)k=﹣2,﹣2.(2)方程的根为x2=x2=2.19、(1)![]() ;(1)-1.20、 (1)一次函数的解析式为:y=3x+6;(2)△AOB的面积=
;(1)-1.20、 (1)一次函数的解析式为:y=3x+6;(2)△AOB的面积=![]() ×6×2=6.21、(1)
×6×2=6.21、(1)![]() ,完成此工程共需9天;(2)6万元.22、(1)
,完成此工程共需9天;(2)6万元.22、(1)![]() ;(2)速度为:
;(2)速度为:![]() km/h,a=
km/h,a=![]() ;(3)接下来一段路程他的速度至少为13.5km/h.23、 (1)
;(3)接下来一段路程他的速度至少为13.5km/h.23、 (1)![]() ;(2)
;(2)![]() .24、(1)(x−12)米;(2)
.24、(1)(x−12)米;(2)![]() 的值为20或1.
的值为20或1.
相关试卷
这是一份2023-2024学年江苏省南京鼓楼实验中学数学八上期末检测模拟试题含答案,共7页。试卷主要包含了分式方程+=1的解是,下列计算中正确是,下列命题是真命题的是等内容,欢迎下载使用。
这是一份2022-2023学年江苏省泰州市泰州中学数学七下期末检测模拟试题含答案,共6页。试卷主要包含了如图等内容,欢迎下载使用。
这是一份2022-2023学年江苏省南京市宁海中学数学七下期末学业水平测试模拟试题含答案,共6页。试卷主要包含了下列命题是真命题的是等内容,欢迎下载使用。









