2022-2023学年江苏省兴化市顾庄区三校七下数学期末联考模拟试题含答案

这是一份2022-2023学年江苏省兴化市顾庄区三校七下数学期末联考模拟试题含答案，共7页。试卷主要包含了如果，那么代数式的值为等内容，欢迎下载使用。
2022-2023学年江苏省兴化市顾庄区三校七下数学期末联考模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如图，已知直角坐标系中的点A、B的坐标分别为A（2，4）、B（4，0），且P为AB的中点．若将线段AB向右平移3个单位后，与点P对应的点为Q，则点Q的坐标是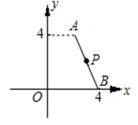（  ）A．（3，2） B．（6，2） C．（6，4） D．（3，5）2．如图，平行四边形、矩形、菱形、正方形的包含关系可用如图表示，则图中阴影部分所表示的图形是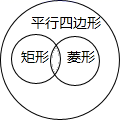（   ）A．矩形         B．菱形      C．矩形或菱形        D．正方形3．如图，分别是矩形的边上的点，将四边形沿直线折叠，点与点重合，点落在点处，已知,则的长是( 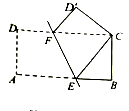  )A．4 B．5 C．6 D．74．下列四组线段中，可以构成直角三角形的是（　　）A．2，3，4 B．3，4，5 C．4，5，6 D．7，8，95．方程3x2﹣7x﹣2＝0的根的情况是（　　）A．方程没有实数根B．方程有两个不相等的实数根C．方程有两个相等的实数很D．不确定6．如图，直线y=-x+2与x轴交于点A，则点A的坐标是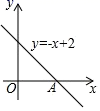（    ）A．（2,0） B．（0,2） C．（1,1） D．（2,2）7．如图，四边形为平行四边形，延长到点，使，连接，，.添加一个条件，不能使四边形成为矩形的是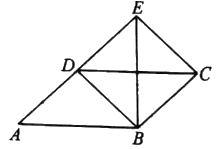（    ）A． B． C． D．8．如果，那么代数式的值为A． B． C． D．9．如图，亮亮书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画了一个与书上完全一样的三角形，那么亮亮画图的依据是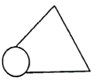（  ）A． B． C． D．10．某商店在节日期间开展优惠促销活动：购买原价超过500元的商品，超过500元的部分可以享受打折优惠．若购买商品的实际付款金额y(单位：元)与商品原价x(单位：元)的函数关系的图像如图所示，则超过500元的部分可以享受的优惠是(  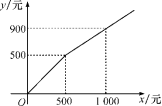  ) A．打六折 B．打七折 C．打八折 D．打九折11．甲、乙两人加工同一种服装，乙每天比甲多加工1件，乙加工服装24件所用时间与甲加工服装20件所用时间相同。设甲每天加工服装x件。由题意可得方程（    ）A． B．C． D．12．矩形，菱形，正方形都具有的性质是（  ）A．对角线相等 B．对角线互相垂直C．对角线互相平分 D．对角线平分一组对角二、填空题（每题4分，满分20分，将答案填在答题纸上）13．勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是把图1放入长方形内得到的，，AB=3，AC=4，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为___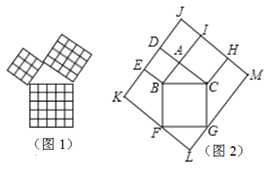．14．在平行四边形ABCD中，若∠A+∠C=140°，则∠B=        ．15．如图，菱形ABCD的对角线相交于点O，若AB＝5，OA＝4，则菱形ABCD的面积_____．16．某食堂午餐供应10元、16元、20元三种价格的盒饭，根据食堂某月销售午餐盒饭的统计图，可计算出该月食堂午餐盒饭的平均价格是_______元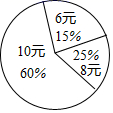．17．当分式有意义时，x的取值范围是__________.三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）如图，正方形ABCD的边长为4，E是线段AB延长线上一动点，连结CE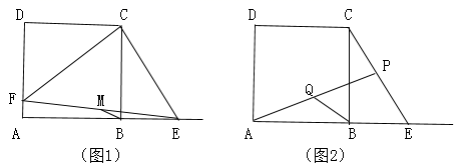．（1）如图1，过点C作CF⊥CE交线段DA于点F．①求证：CF=CE；②若BE=m（0＜m＜4），用含m的代数式表示线段EF的长；（2）在（1）的条件下，设线段EF的中点为M，探索线段BM与AF的数量关系，并用等式表示．（3）如图2，在线段CE上取点P使CP=2，连结AP，取线段AP的中点Q，连结BQ，求线段BQ的最小值．   19．（5分）近些年全国各地频发雾霾天气，给人民群众的身体健康带来了危害，某商场看到商机后决定购进甲、乙两种空气净化器进行销售．若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元，且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同．（1）求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元？（2）若该商场准备进货甲、乙两种空气净化器共30台，且进货花费不超过42000元，问最少进货甲种空气净化器多少台？   20．（8分）积极推行节能减排，倡导绿色出行，“共享单车”、共享助力车”先后上市，为人们出行提供了方便．某人去距离家千米的单位上班，骑“共享助力车”可以比骑“共享单车”少用分钟，已知他骑“共享助力车”的速度是骑“共享单车”的倍，求他骑“共享助力车”上班需多少分钟？   21．（10分）如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC，（1）求证：△ABE≌△ACF；（2）若∠BAE=30°，则∠ADC=　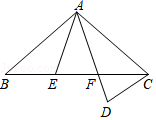   　°．   22．（10分）阅读下列材料：数学课上，老师出示了这样一个问题：如图1，正方形为中，点、在对角线上，且，探究线段、、之间的数量关系，并证明.某学习小组的同学经过思考，交流了自己的想法：小明：“通过观察和度量，发现与存在某种数量关系”；小强：“通过观察和度量，发现图1中线段与相等”；小伟：“通过构造（如图2），证明三角形全等，进而可以得到线段、、之间的数量关系”.老师：“此题可以修改为‘正方形中，点在对角线上，延长交于点，在上取一点，连接（如图3）.如果给出、的数量关系与、的数量关系，那么可以求出的值”.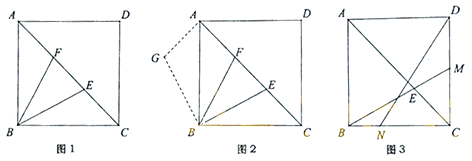请回答：（1）求证：；（2）探究线段、、之间的数量关系，并证明；（3）若，，求的值（用含的代数式表示）.   23．（12分）解分式方程：﹣1=．   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、B2、D3、B4、B5、B6、A7、C8、A9、C10、C11、C12、C 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、11014、110°15、316、1317、 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）①详见解析；②；（2）BM= AF；（3）19、（1）每台甲种空气净化器、每台乙种空气净化器的进价分别为1200元，1500元（2）至少进货甲种空气净化器10台．20、20分钟21、（1）证明见解析；（2）1．22、（1）详见解析；（2），证明详见解析；（3）23、分式方程的解为x=1.1．