


2022-2023学年江苏省常州市教育会业水平监测七年级数学第二学期期末学业质量监测试题含答案
展开
这是一份2022-2023学年江苏省常州市教育会业水平监测七年级数学第二学期期末学业质量监测试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,已知,下列说法,你认为正确的是等内容,欢迎下载使用。
2022-2023学年江苏省常州市教育会业水平监测七年级数学第二学期期末学业质量监测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.![]() 的取值范围如数轴所示,化简
的取值范围如数轴所示,化简![]() 的结果是( )
的结果是( )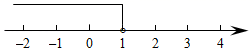 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.已知
2.已知![]() (a≠0,b≠0),下列变形错误的是( )A.
(a≠0,b≠0),下列变形错误的是( )A.![]() B.2a=3b C.
B.2a=3b C.![]() D.3a=2b3.如图,在四边形
D.3a=2b3.如图,在四边形![]() 中,
中,![]() ,点
,点![]() 分别为线段
分别为线段![]() 上的动点(含端点,但点
上的动点(含端点,但点![]() 不与点
不与点![]() 重合),点
重合),点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 长度的最大值为( )
长度的最大值为( )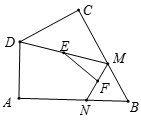 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如果一个直角三角形的两条边长分别为
4.如果一个直角三角形的两条边长分别为![]() 和
和![]() ,那么这个三角形的第三边长为( )A.
,那么这个三角形的第三边长为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]() 5.用一些相同的正方形,摆成如下的一些大正方形,如图第(1)个图中小正方形只有一个,且阴影面积为1,第(2)个图中阴影小正方形面积和3;第(3)个图中阴影小正方形面积和为5,第(9)个图中阴影小正方形面积和为( )
5.用一些相同的正方形,摆成如下的一些大正方形,如图第(1)个图中小正方形只有一个,且阴影面积为1,第(2)个图中阴影小正方形面积和3;第(3)个图中阴影小正方形面积和为5,第(9)个图中阴影小正方形面积和为( )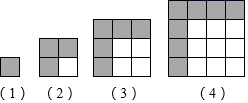 A.11 B.13 C.15 D.176.已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是
A.11 B.13 C.15 D.176.已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是![]()
![]() A.
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]() 7.下列四组线段中,可以构成直角三角形的是( )A.1,2,3 B.4,5,6 C.9,12,15 D.
7.下列四组线段中,可以构成直角三角形的是( )A.1,2,3 B.4,5,6 C.9,12,15 D.![]() 8.下列说法,你认为正确的是( )A.0 的倒数是 0 B.3-1=-3 C.是有理数 D.
8.下列说法,你认为正确的是( )A.0 的倒数是 0 B.3-1=-3 C.是有理数 D.![]() 39.甲、乙两人各射击
39.甲、乙两人各射击![]() 次,甲所中的环数是
次,甲所中的环数是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且甲所中的环数的平均数是
,且甲所中的环数的平均数是![]() ,众数是
,众数是![]() ;乙所中的环数的平均数是
;乙所中的环数的平均数是![]() ,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )A.甲射击成绩比乙稳定 B.乙射击成绩比甲稳定C.甲,乙射击成绩稳定性相同 D.甲、乙射击成绩稳定性无法比较10.如果一组数据
,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )A.甲射击成绩比乙稳定 B.乙射击成绩比甲稳定C.甲,乙射击成绩稳定性相同 D.甲、乙射击成绩稳定性无法比较10.如果一组数据![]() ,
,![]() ,0,1,x,6,9,12的平均数为3,则x为
,0,1,x,6,9,12的平均数为3,则x为![]()
![]() A.2 B.3 C.
A.2 B.3 C.![]() D.111.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )
D.111.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )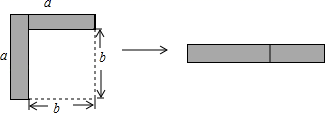 A.(a﹣b)2=a2﹣2ab+b2 B.a(a﹣b)=a2﹣abC.(a﹣b)2=a2﹣b2 D.a2﹣b2=(a+b)(a﹣b)12.正比例函数
A.(a﹣b)2=a2﹣2ab+b2 B.a(a﹣b)=a2﹣abC.(a﹣b)2=a2﹣b2 D.a2﹣b2=(a+b)(a﹣b)12.正比例函数![]() 的图象上有两点
的图象上有两点![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系是( )A.
的大小关系是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在△ABC中,AB=5,BC=7,EF是△ABC的中位线,则EF的长度范围是________.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在△ABC中,AB=5,BC=7,EF是△ABC的中位线,则EF的长度范围是________.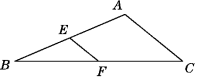 14.如图,直线y=kx+3经过点A(1,2),则它与x轴的交点B的坐标为____.
14.如图,直线y=kx+3经过点A(1,2),则它与x轴的交点B的坐标为____.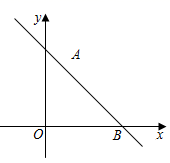 15.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.
15.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.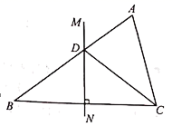 16.如图,已知
16.如图,已知![]() ,
,![]() ,
,![]() ,
,![]() ,若线段
,若线段![]() 可由线段
可由线段![]() 围绕旋转中心
围绕旋转中心![]() 旋转而得,则旋转中心
旋转而得,则旋转中心![]() 的坐标是______.
的坐标是______.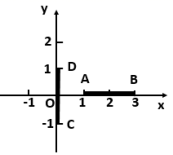 17.如图,已知点A(1,a)与点B(b,1)在反比例函数y=
17.如图,已知点A(1,a)与点B(b,1)在反比例函数y=![]() (x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.
(x>0)图象上,点P(m,0)是x轴上的任意一点,若△PAB的面积为2,此时m的值是______.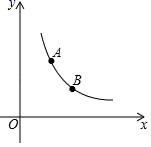 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)先化简,再求值:
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)先化简,再求值:![]() ,其中 a 满足
,其中 a 满足![]() . 19.(5分)已知反比例函数y=
. 19.(5分)已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D(1)求这个反比函数的表达式;(2)求△ACD的面积.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D(1)求这个反比函数的表达式;(2)求△ACD的面积.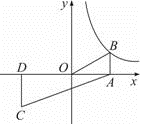 20.(8分)实践与探究宽与长的比是
20.(8分)实践与探究宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。下面我们通过折纸得到黄金矩形。第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。下面我们通过折纸得到黄金矩形。第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。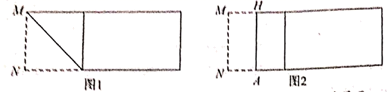 第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是
第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。第三步,折出内侧矩形的对角线
。第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
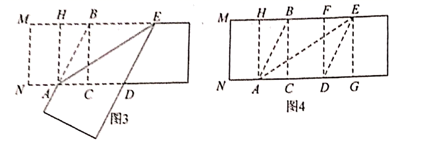
处,折痕为![]() 。第四步,展平纸片,按照所得的点
。第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。 (1)上述第三步将
(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。(2)上述第四步折出折痕
的形状,并说明理由。(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形
的长度为2)(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
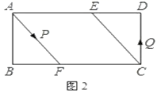
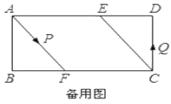
除外,直接写出答案,不需证明,可能参考数值:![]() )(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________. 21.(10分)已知,矩形
)(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________. 21.(10分)已知,矩形![]() 中,
中,![]() ,
,![]() 的垂直平分
的垂直平分![]() 线分别交
线分别交![]() 于点
于点![]() ,垂足为
,垂足为![]() .(1)如图1,连接
.(1)如图1,连接![]() ,求证:四边形
,求证:四边形![]() 为菱形;(2)如图2,动点
为菱形;(2)如图2,动点![]() 分别从
分别从![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周,即点
各边匀速运动一周,即点![]() 自
自![]() 停止,点
停止,点![]() 自
自![]() 停止.在运动过程中,①已知点
停止.在运动过程中,①已知点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 四点为顶点的四边形是平行四边形时,则
四点为顶点的四边形是平行四边形时,则![]() ____________.②若点
____________.②若点![]() 的运动路程分别为
的运动路程分别为![]() (单位:
(单位:![]() ),已知
),已知![]() 四点为顶点的四边形是平行四边形,则
四点为顶点的四边形是平行四边形,则![]() 与
与![]() 满足的数量关系式为____________.
满足的数量关系式为____________.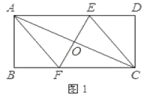
 22.(10分)如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点. (1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.
22.(10分)如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点. (1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.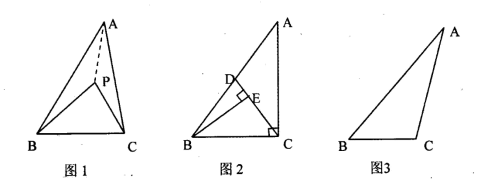 23.(12分)如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.(1)如图1,点A、D分别在EH和EF上,连接BH、AF,直接写出BH和AF的数量关系;(2)将正方形EFGH绕点E顺时针方向旋转.①如图2,判断BH和AF的数量关系,并说明理由;②如果四边形ABDH是平行四边形,请在备用图中补全图形;如果四方形ABCD的边长为
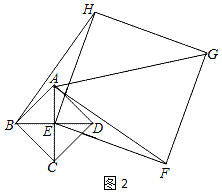
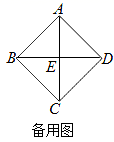
23.(12分)如图1,已知四边形ABCD是正方形,对角线AC、BD相交于点E,以点E为顶点作正方形EFGH.(1)如图1,点A、D分别在EH和EF上,连接BH、AF,直接写出BH和AF的数量关系;(2)将正方形EFGH绕点E顺时针方向旋转.①如图2,判断BH和AF的数量关系,并说明理由;②如果四边形ABDH是平行四边形,请在备用图中补全图形;如果四方形ABCD的边长为![]() ,求正方形EFGH的边长.
,求正方形EFGH的边长.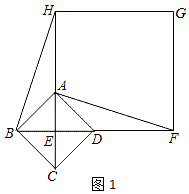
 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、D5、D6、B7、C8、D9、B10、D11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、1<EF<614、(3,0)15、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、D2、B3、B4、D5、D6、B7、C8、D9、B10、D11、D12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、1<EF<614、(3,0)15、![]() 16、
16、![]() 或
或![]() 17、﹣1或3 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、
17、﹣1或3 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、![]() ,
,![]() .19、(1 )
.19、(1 )![]() ;(2)6.20、(1)四边形
;(2)6.20、(1)四边形![]() 是菱形,见解析;(2)见解析;(3)黄金矩形
是菱形,见解析;(2)见解析;(3)黄金矩形![]() (或黄金矩形
(或黄金矩形![]() );(4)希腊的巴特农神庙(或巴黎圣母院).21、(1)见解析;(2)①
);(4)希腊的巴特农神庙(或巴黎圣母院).21、(1)见解析;(2)①![]() ;②
;②![]() 22、(1)详见解析;(2)
22、(1)详见解析;(2)![]() 23、(1)见解析;(2)①BH=AF,理由见解析,②正方形EFGH的边长为
23、(1)见解析;(2)①BH=AF,理由见解析,②正方形EFGH的边长为![]() .
.
相关试卷
这是一份2023-2024学年江苏省常州市教育会业水平监测数学九年级第一学期期末检测试题含答案,共8页。
这是一份江苏省常州市教育会业水平监测2023-2024学年数学八年级第一学期期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,已知 ,则下列不等式中正确的是等内容,欢迎下载使用。
这是一份2023-2024学年江苏省常州市勤业中学数学八上期末学业质量监测模拟试题含答案,共8页。试卷主要包含了下列命题是假命题的是等内容,欢迎下载使用。








