2022-2023学年江苏省扬州市高邮市数学七年级第二学期期末调研模拟试题含答案

2022-2023学年江苏省扬州市高邮市数学七年级第二学期期末调研模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．估计的运算结果在哪两个整数之间（　　）

A．3和4 B．4和5 C．5和6 D．6和7

2．下列方程中，一元二次方程的是（　　）

A．＝0 B．（2x+1）（x﹣3）＝1

C．ax2+bx＝0 D．3x2﹣2xy﹣5y2＝0

3．如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：

甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．

乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．

根据两人的作法可判断（）

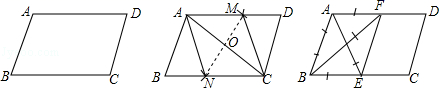
A．甲正确，乙错误 B．乙正确，甲错误 C．甲、乙均正确 D．甲、乙均错误

4．在平行四边形中cm，cm，则平行四边形的周长为(    )

A．cm B．cm C．cm D．cm

5．函数中自变量x的取值范围是（  ）

A．x≥ 1        B．x≤ 1         C．x≠ 1           D．x＞ 1

6．如图所示，正方形纸片ABCD中，对角线AC，BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB，AC于点E，G，连接GF，给出下列结论：

①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数有（）

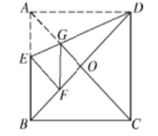
A．2个 B．4个 C．3个 D．5个

7．若一次函数的图象经过第一、二、四象限，则下列不等式一定成立的是（        ）

A． B． C． D．

8．下面几组条件中，能判断一个四边形是平行四边形的是（　　）

A．一组对边相等 B．两条对角线互相平分

C．一组对边平行 D．两条对角线互相垂直

9．一个多边形的内角和是7200，则这个多边形的边数是(     )

A．2 B．4 C．6 D．8

10．反比例函数y＝，当x的值由n（n＞0）增加到n+2时，y的值减少3，则k的值为（　　）

A． B． C．﹣ D．

11．甲、乙、丙、丁参加体育训练，近期10次跳绳测试的平均成绩都是每分钟174个，其方差如下表：

则这10次跳绳中，这四个人发挥最稳定的是（ ）

A．甲 B．乙 C．丙 D．丁

12．使函数y＝有意义的自变量x的取值范围是（　　）

A．x≥6 B．x≥0 C．x≤6 D．x≤0

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．函数中，自变量的取值范围是_____．

14．函数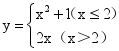,则当函数值y=8时,自变量x的值是_____.

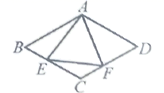
15．已知，菱形中，、分别是、上的点，且，，则__________度．

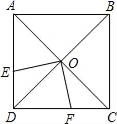
16．已知：如图，正方形ABCD中，对角线AC和BD相交于点O．E、F分别是边AD、CD上的点，若AE＝4cm，CF＝3cm，且OE⊥OF，则EF的长为_____cm．

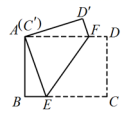
17．如图，在矩形ABCD中，AB=6cm，BC=8cm，现将其沿EF对折，使得点C与点A重合，点D落在处，AF的长为___________．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）2019年3月21日，长春市遭遇了一次大量降雪天气，市环保系统出动了多辆清雪车连夜清雪，已知一台大型清雪车比一台小型清雪车每小时多清扫路面6千米，一台大型清雪车清扫路面90千米与一台小型清雪车清扫路面60千米所用的时间相同．求一台小型清雪车每小时清扫路面的长度．

19．（5分）把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点B重合，联结DF，点M，N分别为DF，EF的中点，联结MA，MN．

（1）如图1，点E，F分别在正方形的边CB，AB上，请判断MA，MN的数量关系和位置关系，直接

写出结论；

（2）如图2，点E，F分别在正方形的边CB，AB的延长线上，其他条件不变，那么你在（1）中得到的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

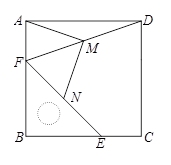
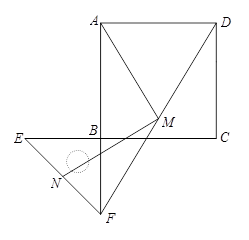
图1                            图2

20．（8分）某商店一种商品的定价为每件50元.商店为了促销，决定如果购买5件以上，则超过5件的部分打七折.

（1）用表达式表示购买这种商品的货款（元）与购买数量（件）之间的函数关系；

（2）当，时，货款分别为多少元？

21．（10分）某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛，在最近的四次专题测试中，他们三人的成绩如下表所示：

（1）请算出小红的平均分为多少？

（2）该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重，权重比依次为x：1：2：1，最后得出三人的成绩（加权平均数），若从高分到低分排序为小亮、小明、小红，求正整数x的值．

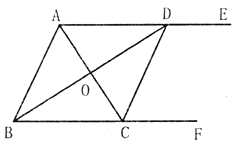
22．（10分）如图，，平分交于点，于点，交于点，连接，求证：四边形是菱形．

23．（12分）一种五米种子的价格为5元/kg，A如果一次购买2kg以上的种子，超过2kg部分的种子价格打八折．

（1）填写表：

（2）写出付款金额关于购买量的函数解析式，并画出函数图象．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、B

3、C

4、D

5、A

6、C

7、D

8、B

9、C

10、D

11、B

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、或4

15、

16、1

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、12千米

19、（1）MA=MN，MA⊥MN；（2）成立，理由详见解析

20、（1）;（2）150元; 425元.

21、（1）77.5分；（2）1

22、见解析

23、（1）2.5、5、7.5、10、12、14、16、18；（2）