2022-2023学年江苏省扬州市仪征市大仪中学七下数学期末预测试题含答案

这是一份2022-2023学年江苏省扬州市仪征市大仪中学七下数学期末预测试题含答案，共7页。试卷主要包含了不等式组的解集是，在五张完全相同的卡片上分别画上等内容，欢迎下载使用。
2022-2023学年江苏省扬州市仪征市大仪中学七下数学期末预测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．数据3，2，0，1，的方差等于（    ）A．0 B．1 C．2 D．32．如图，将点P（-1，3）向右平移n个单位后落在直线y=2x-1上的点P′处，则n等于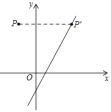（　　）A．2 B． C．3 D．43．在代数式，，，﹣b，中，是分式的个数为（　　）A．1个 B．2个 C．3个 D．4个4．不等式组的解集是（    ）A． B． C． D．5．已知平行四边形中，一个内角，那么它的邻角（    ）.A． B． C． D．6．在五张完全相同的卡片上分别画上：等边三角形、平行四边形、等腰梯形、圆和正方形，在看不见图形的情况下随机抽出1张卡片，这张卡片上的图形是中心对称图形的概率是（　　）A． B． C． D．7．根据图1所示的程序，得到了如图y与x的函数图像，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴交图像于点P、Q，连接OP、OQ．则以下结论：①x<0 时，y=；②△OPQ的面积为定值；③x>0时，y随x的增大而增大；④MQ=2PM⑤∠POQ可以等于90°．其中正确结论序号是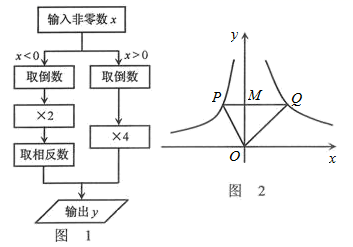（    ）A．①②③ B．②③④ C．③④⑤ D．②④⑤8．（2011•潼南县）目前，全球淡水资源日益减少，提倡全社会节约用水．据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升．小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是（　　） A、y=0.05x  B、y=5x C、y=100x  D、y=0.05x+1009．下图是某同学在沙滩上用石子摆成的小房子．观察图形的变化规律，第6个小房子用的石子数量为 (    )A．87 B．77 C．70 D．6010．如图，在矩形中，对角线，交于点，已知，，则的长为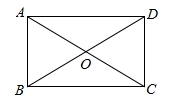（  ）A．2 B．4 C．6 D．811．如果与最简二次根式是同类二次根式，则的值是(    )A． B． C． D．12．《国家宝藏》节目立足于中华文化宝库资源，通过对文物的梳理与总结，演绎文物背后的故事与历史，让更多的观众走进博物馆，让一个个馆藏文物鲜活起来．下面四幅图是我国一些博物馆的标志，其中是中心对称图形的是（    ）．A． B． C． D．二、填空题（每题4分，满分20分，将答案填在答题纸上）13．小明参加岗位应聘中，专业知识、工作经验、仪表形象三项的得分分别为：分、分、分．若这三项的重要性之比为，则他最终得分是_________分．14．如图，在ΔABC中，AB=8，AC=6，∠BAC=30°，将ΔABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为________.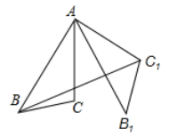15．若一组数据1，3，5，，的众数是3，则这组数据的方差为______.16．在一个不透明的袋子中有若千个小球，这些球除颜色外无其他差别，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，然后把它重新放回袋中并摇匀，不断重复上述过程．以下是利用计算机模拟的摸球试验统计表：摸球实验次数100100050001000050000100000“摸出黑球”的次数36387201940091997040008“摸出黑球”的频率（结果保留小数点后三位）0.3600.3870.4040.4010.3990.400根据试验所得数据，估计“摸出黑球”的概率是_______（结果保留小数点后一位）．17．的平方根是____．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）解方程：x2﹣6x﹣4＝1．   19．（5分）如图，在四边形中，，，，为的中点，连接.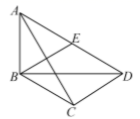（1）求证：四边形是菱形；（2）连接，若平分，，求的长.   20．（8分）（课题研究）旋转图形中对应线段所在直线的夹角（小于等于的角）与旋转角的关系．（问题初探）线段绕点顺时针旋转得线段，其中点与点对应，点与点对应，旋转角的度数为，且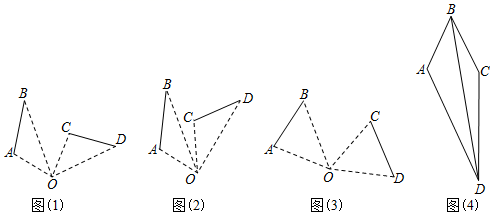．（1）如图（1）当时，线段、所在直线夹角为______．（2）如图（2）当时，线段、所在直线夹角为_____．（3）如图（3），当时，直线与直线夹角与旋转角存在着怎样的数量关系？请说明理由；（形成结论）旋转图形中，当旋转角小于平角时，对应线段所在直线的夹角与旋转角_____．（运用拓广）运用所形成的结论求解下面的问题：（4）如图（4），四边形中，，，，，，试求的长度．   21．（10分）计算化简(1)                (2)   22．（10分）如图甲，在等边三角形ABC内有一点P，且PA＝2，PB＝，PC＝1，求∠BPC度数的大小和等边三角形ABC的边长．解题思路是：将△BPC绕点B逆时针旋转60°，如图乙所示，连接PP′．（1）△P′PB是   三角形，△PP′A是   三角形，∠BPC＝   °；（2）利用△BPC可以求出△ABC的边长为   ．如图丙，在正方形ABCD内有一点P，且PA＝，BP＝，PC＝1；（3）求∠BPC度数的大小；（4）求正方形ABCD的边长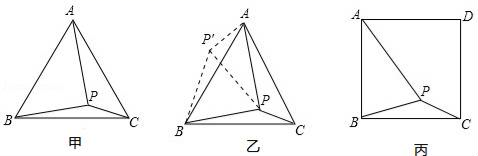．   23．（12分）八年级（1）班同学为了解某小区家庭月均用水情况，随机调査了该小区部分家庭，并将调查数据整理成如下两幅不完整的统计图表：月均用水量x（t）频数（户）频率0＜x≤560.125＜x≤10m0.2410＜x≤15160.3215＜x≤20100.2020＜x≤254n25＜x≤3020.04请根据以上信息，解答以下问题：（1）直接写出频数分布表中的m、n的值并把频数直方图补充完整；（2）求出该班调查的家庭总户数是多少？（3）求该小区用水量不超过15的家庭的频率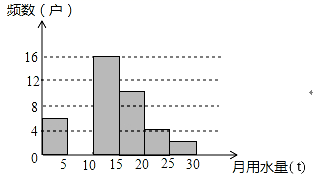．   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、C2、C3、B4、A5、C6、C7、D8、：解：y=100×0.05x，即y=5x．故选B．9、D10、B11、B12、A 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、15.114、10.15、216、0.117、±3 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、x1=3+，x2=3﹣．19、（1）详见解析；（2）20、（1）90°；（2）60°；（3）互补，理由见解析；相等或互补；（4）.21、（1）（2）22、（1）等边  直角  150°；（2）；（3）135°；（4） .23、（1）m=12,n=0.08;（2）50；（3）0.68.